数学代写|数学建模代写Mathematical Modeling代考|TMA4195 Modelling Tasks

如果你也在 怎样代写数学建模Mathematical Modeling TMA4195这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。数学建模Mathematical Modeling是使用数学概念和语言对一个具体系统的抽象描述。建立数学模型的过程被称为数学建模。数学模型被用于自然科学（如物理学、生物学、地球科学、化学）和工程学科（如计算机科学、电气工程），以及非物理系统，如社会科学（如经济学、心理学、社会学、政治学）。使用数学模型来解决商业或军事行动中的问题是运筹学领域的一个重要部分。数学模型也被用于音乐、语言学、和哲学（例如，集中用于分析哲学）。

数学建模Mathematical Modeling可以有很多形式，包括动态系统、统计模型、微分方程或博弈论模型。这些和其他类型的模型可以重叠，一个特定的模型涉及各种抽象结构。一般来说，数学模型可能包括逻辑模型。在许多情况下，一个科学领域的质量取决于在理论方面开发的数学模型与可重复的实验结果的吻合程度。理论上的数学模型和实验测量结果之间缺乏一致性，往往导致更好的理论被开发出来，从而取得重要进展。

数学建模Mathematical Modeling代写，免费提交作业要求， 满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕 博写手团队，所有订单可靠准时，保证 100% 原创。 最高质量的数学建模Mathematical Modeling作业代写，服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。 由于作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此数学建模Mathematical Modeling作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

数学代写|数学建模代写Mathematical Modeling代考|Modelling Tasks

Modelling tasks are messy problem solving questions that are situated in reality. Barbosa (2006) describes modelling tasks as problematic activities that, although not purely mathematical, require modellers to investigate the situation “with reference to reality via mathematics” (p. 294), and relate what happens in reality to mathematics by applying their mathematical knowledge and skills to determine a possible solution to the problem. As such, modellers need to combine their knowledge of mathematics with their knowledge from outside of mathematics (such as their lived-experiences) to produce a realistic and meaningful solution.

Modelling tasks can be classified based on a variety of classification schemes $(\mathrm{Maa} 2010)$ :

1. Modelling activity, where tasks may focus on the entire or a part of the modelling process and can promote modellers’ understanding of the steps taken to solve a modelling task;
2. Data, where tasks require modellers to investigate and critically decide the information relevant to solve the task, and/or to acquire the missing information required to solve the task;
3. Nature of relationship to reality, where tasks range from fantasies to genuine context only;Situations, where tasks are classified based on their relationship between the modeller’s life and the context of the task. This may range from personal (closest to a modeller’s life), to educational/occupational, public, and scientific (furthest away from a modeller’s life);
4. Type of model used, including descriptive models, which describe the situation as close to reality as possible; and normative models, which only describe certain aspects of reality while ignoring other aspects;
5. Type of representation, where tasks are presented as text; pictures; text and pictures; printed materials; and situations;
6. Openness, where tasks are classified based on the final product produced by modellers;
7. Cognitive demand, which include tasks that focus on extra-mathematical modelling, inner-mathematical working, “Grundvorstellungen” (mental objects that help with the transitions between reality and the world of mathematics), dealing with texts containing mathematics, mathematical reasoning, and dealing with mathematical representations;
8. And mathematical content, where tasks are classified based on their mathematical demands and their audience.

数学代写|数学建模代写Mathematical Modeling代考|Modelling Cycles

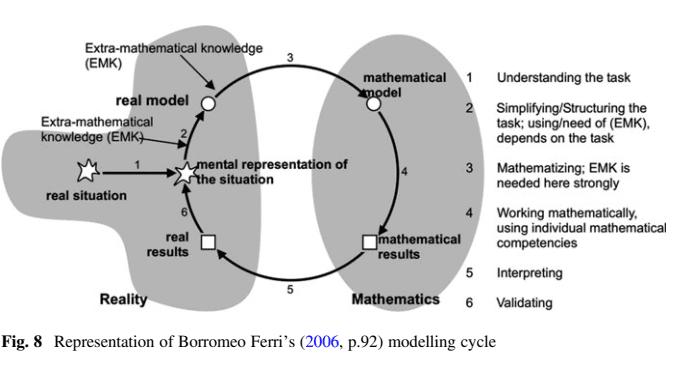
The process to solve modelling tasks can be referred to as a modelling cycle. Modelling cycles describe general modelling behaviors and can be illustrated through the use of various diagrammatic representations (Blum and Lei $\beta$ 2005; Borromeo Ferri 2006; Kaiser 2005; Mason and Davis 1991; Pollak 1979). These diagrams “illustrate key stages in an iterative process that commences with a real world problem and ends with the report of a successful solution, or a decision to revisit the model to achieve a better outcome” (Galbraith 2012, p. 8). For the purpose of this study, we use Borromeo Ferri’s modelling cycle as a unit of analysis.

Borromeo Ferri $(2006,2010)$ describes the modelling cycle from a cognitive perspective, and focuses on modellers’ individual thinking processes, where these processes are made explicit through modellers’ actions during their modelling processes (see Fig. 8). Borromeo Ferri’s (2006) modelling cycle begins with a scenario situated within reality. As modellers interpret the real situation, they build a “visual, verbal, auditive, or formal” (Borromeo Ferri 2010, p.104) mental representation of the situation (MRS). MRS highlights the mental process modellers go through to understand the task, which happens on an implicit level, and is dependent on the modeller’s thinking style and experiences (Borromeo Ferri 2010).

In the formation of a MRS, modellers may make connections with and simplify the original situation and discuss with each other the approach of the problem. Therefore, a MRS is a representation of modellers’ thinking process, a demonstration of modellers’ understanding and interpretation of the situation, and an illustration of the direction in which modellers take to solve the problem. After modellers create a MRS, they make further assumptions of the situation and draw on their lived-experiences to create a real model to represent the situation. Borromeo Ferri (2006) refers to these lived-experiences as extra-mathematical knowledge (EMK). EMK includes any knowledge or experiences that originate from outside of a modellers’ mathematical experiences. EMK may have little or no clear connections to mathematics, but plays an essential role in the modelling process, as it enables modellers to consider the problem situation from a real world perspective, and allows them to produce a reasonable real model and mathematical model to represent the situation (Blum and Borromeo Ferri 2009; Borromeo Ferri 2006). In the process of building a real model, modellers make decisions on their assumptions about and their approach to the problem situation. A real model may use some mathematics to represent the situation, but also contains the original context. It is strongly connected to the MRS and “contains essential features of the original situation, but is on the other hand already so schematized that (if at all possible) it allows for an approach with mathematical means” (Blum and Niss 1991, p.38).

数学建模代写

数学代写|数学建模代写MATHEMATICAL MODELING代 考|MODELLING TASKS

建模任务是解决现实中的混乱问题。巴博萨2006将建模任务描述为有问题的活动，虽然不是纯粹的数学，但需要建模者“通过数学参考现实”来调 查情况 $p .294$ ，并通过应用他们的数学知识和技能来确定问题的可能解决方案，将现实中发生的事情与数学联系起来。因此，建模者需要将他们的 数学知识与数学以外的知识结合起来suchastheirlived – experiences产生一个现实和有意义的解决方案。
建模任务可以基于多种分类方案进行分类(Maa2010):

1. 建模活动，其中任务可能集中于整个或部分建模过程，并且可以促进建模者对解决建模任务所采取的步骙的理解；
2. 数据，任务要求建模者调查和批判性地决定与解仜任务相关的信息，和/或获取解决任务所需的缺失信息；
3. 与现实的关系的性质，任务范围从幻想到真实的上下文；情境，任务根据建模者的生活与任务上下文之间的关系进行分类。这可能包括个人 closesttoamodeller’slife，教育/职业，公共和科学furthestaway fromamodeller’slife;
4. 使用的模型类型，包括描述性模型，描述尽可能接近现实的情况；和规范模型，它们只描述现实的某些方面而忽略其他方面；
5. 表示类型，其中任务以文本形式呈现；图片;文字和图片；印刷材料；和情况；
6. 开放性，任务根据建模者生产的最终产品进行分类；
   7.认知需求，包括专注于非数学建模、内部数学工作、“rundvorstellungen”的任务
   mentalobjectsthathelpwiththetransitionsbetweenrealityandtheworldofmathematics、处理包含数学、数学推理的文本，以及处 理数学表示;
7. 和数学内容，其中任务根据他们的数学需求和他们的听众分类。

数学代写|数学建模代写MATHEMATICAL MODELING代考|MODELLING CYCLES

解决建模任务的过程可以称为建模周期。建模周期描述了一般的建模行为，可以通过使用各种图表表示来说明
BlumandLei $\beta \$ 2005$; BorromeoFerri2006; Kaiser 2005; MasonandDavis1991; Pollak1979. 这些图表“说明了迭代过程中的关键阶段， 从现实世界的问题开始，到成功解决方案的报告结束，或者决定重新访问模型以获得更好的结果”Galbraith $2012, p .8$. 出于本研究的目的，我们 使用 Borromeo Ferri 的建模周期作为分析单元。
博罗梅血·费里 $(2006,2010)$ 从认知的角度描述建模周期，并关注建模者的个人思维过程，这些过程通过建模者在建模过程中的行为而变得明确 seeFig. 8. Borromeo Ferri 的2006建模周期从位于现实中的场景开始。当建模者解释真实情况时，他们构建了一个 “视觉、口头、听觉或正式的” BorromeoFerri $2010, p$.104情境的心理表征 MRS. MRS 突出了建模者理解任务所经历的心理过程，这是在隐含的层面上发生的，并且取决于建 模者的思维方式和经验BorromeoFerri 2010 .
在MRS的形成过程中，建模者可以联系并简化原始情况，并相互讨论解决问题的方法。因此，MRS是建模者思维过程的表征，是建模者对情境的理 解和解释的展示，是建模者解决问题的方向的说明。建模者创建 MRS 后，他们会进一步假设情况并利用他们的生活经验来创建真实模型来表示情 况。博罗梅奧.费里 2006 将这些生活经验称为超数学知识 $E M K$. EMK包括源自建模者数学经验之外的任何知识或经验。EMK可能与数学没有或几 乎没有明确的联系，但在建模过程中起着至关重要的作用，因为它使建模者能够从现实世界的角度考虑问题情况，并使他们能够产生合理的真实 模型和数学模型来表示情况BlumandBorromeoFerri2009; BorromeoFerri2006. 在构建真实模型的过程中，建模者根据他们对问题情况的假 设和方法做出决策。一个真实的模型可能使用一些数学来表示情况，但也包含原始上下文。它与 MRS 密切相关，“包含原始情况的基本特征，但另 一方面已经如此图式化，以至于ifatallpossible 它允许采用数学方法” BlumandNiss1991, p.38.

数学代写|数学建模代写Mathematical Modeling代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。