数学代写|ST308 Bayesian Analysis

The first model we will fit to the contraceptives data is a varying-intercept logistic regression model, where the intercept varies by district.
Prior distribution:
$\beta_{0 j} \sim N\left(\mu_0, \sigma_0\right)$, with $\mu_0 \sim N(0,100)$ and $\sigma_0 \sim \operatorname{Exponential}(.1)$
$$
\beta_1 \sim N(0,100), \beta_2 \sim N(0,100), \beta_3 \sim N(0,100)
$$
Model for data:
$$
\begin{aligned}
& Y_{i j} \sim \operatorname{Bernoulli}\left(p_{i j}\right) \
& \text { logit } p_{i j}=\beta_{0 j}+\beta_1 * \text { urban }+\beta_2 * \text { living-children }+\beta_3 * \text { age-mean }
\end{aligned}
$$

where $Y_{i j}$ is 1 if woman $i$ in district $j$ uses contraception, and 0 otherwise, and where $i=1, \ldots, N$ and $j=1, \ldots, J$ ( $N$ is the number of observations in the data, and $J$ is the number of districts). The above notation assumes $N(\mu, \sigma)$ is a normal distribution with mean $\mu$ and standard deviation $\sigma$. Also, the above notation assumes $\operatorname{Exponential}(\lambda)$ has mean $1 / \lambda$. These are consistent with the parameterizations in Stan.
After you read the train and test data into $\mathrm{R}$, the following code will help with formatting:
# convert everything to numeric
for (i in 1 :ncol(train)) {
train $[, i]<-$ as.numeric(as.character(train $[, i]))$
test $[, i]<-$ as.numeric(as.character(test $[, i]))$
}
# map district 61 to 54 (so that districts are in order)
train_bad_indices <- which(train $\$$ district $==61$ )
train[train_bad_indices, 1$]<-54$
test_bad_indices <- which(test $\$$ district $==61$ )
test[test_bad_indices, 1$]<-54$

(b) Fit the varying-intercept model specified above to your simulated data
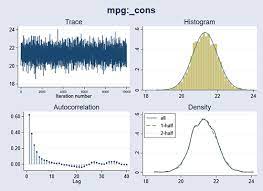
(c) Plot the trace plots of the MCMC sampler for the parameters $\mu_{\beta_0}, \sigma_{\beta_0}, \beta_1, \beta_2, \beta_3$. Does it look like the samplers converged?
(d) Plot histograms of the posterior distributions for the parameters $\beta_{0,10}, \beta_{0,20} \ldots \beta_{0,60}$. Are the actual parameters that you generated contained within these posterior distributions?
We now fit our model to the actual data.
(e) Fit the varying-intercept model to the real train data. Make sure to set a seed at 46 within the Stan function, to ensure that you will get the same results if you fit your model correctly.
(f) Check the convergence by examining the trace plots, as you did with the simulated data.
(g) Based on the posterior means, women belonging to which district are most likely to use contraceptives? Women belonging to which district are least likely to use contraceptives?

(h) What are the posterior means of $\mu_{\beta_0}$ and $\sigma_{\beta_0}$ ? Do these values offer any evidence in support of or against the varying-intercept model?

In the next model we will fit to the contraceptives data is a varying-coefficients logistic regression model, where the coefficients on living-children, age-mean and urban vary by district:
Prior distribution:
$\beta_{0 j} \sim N\left(\mu_0, \sigma_0\right)$, with $\mu_0 \sim N(0,100)$ and $\sigma_0 \sim \operatorname{Exponential}(0.1)$
$\beta_{1 j} \sim N\left(0, \sigma_1\right)$, with $\sigma_1 \sim \operatorname{Exponential}(0.1)$
$\beta_{2 j} \sim N\left(0, \sigma_2\right)$, with $\sigma_2 \sim \operatorname{Exponential}(0.1)$
$\beta_{3 j} \sim N\left(0, \sigma_3\right)$, with $\sigma_3 \sim \operatorname{Exponential}(0.1)$
Model for data:
$Y_{i j} \sim \operatorname{Bernoulli}\left(p_{i j}\right)$
$\operatorname{logit} p_{i j}=\beta_{0 j}+\beta_{1 j}$ urban $+\beta_{2 j}$ age-mean $+\beta_{3 j}$ living-children
where $i=1, \ldots, N$ and $j=1, \ldots, J(N$ is the number of observations in the data, and $J$ is the number of districts).
(a) Fit the model to the real data. For each of the three coefficients to the predictors, plot vertical segments corresponding to the $95 \%$ central posterior intervals for the coefficient within each district. Thus you should have 60 parallel segments on each graph. If the segments are overlapping on the vertical scale, then the model fit suggests that the coefficient does not differ by district. What do you conclude from these graphs?
(b) Use all of the information you’ve gleaned thus far to build a final Bayesian logistic regression classifier on the train set. Then, use your model to make predictions on the test set. Report your model’s classification percentage.

We now fit our model to the actual data.
(e) Fit the varying-intercept model to the real train data. Make sure to set a seed at 46 within the Stan function, to ensure that you will get the same results if you fit your model correctly.
(f) Check the convergence by examining the trace plots, as you did with the simulated data.
(g) Based on the posterior means, women belonging to which district are most likely to use contraceptives? Women belonging to which district are least likely to use contraceptives?

(h) What are the posterior means of $\mu_{\beta_0}$ and $\sigma_{\beta_0}$ ? Do these values offer any evidence in support of or against the varying-intercept model?

In Major League Baseball (MLB), each team plays 162 games in the regular season. The data in Bayesball.txt contains information about every regular season game in 2017. The data can be read in by the command
games2017 = read.table (“Bayesball.txt”, sep=’ ,’)
The relevant columns of the data are
data2017 = games2017 $[, c(7,4,11,10)]$
names (data_2017) $=c($ “Home”, “Away”, “Home_Score”, “Away_Score”)

Because we are going to focus on wins versus losses, you will need to convert these data into binary outcomes.

Under the Bradley-Terry model, each team $i$ is assumed to have some underlying talent parameter $\pi_i$. The model states that the probability that team $i$ defeats opponent $j$ in any game is:
$$
\operatorname{Pr}(\text { team } i \text { defeats team } j)=\frac{\pi_i}{\pi_i+\pi_j} \text {. }
$$
where $i, j \in(1,2, \ldots 30)$, since there are 30 teams in MLB. The parameter $\pi_i$ is team $i$ ‘s “strength” parameter, and is required to be positive.

If we let $V_{i j}$ be the number of times in a season that team $i$ defeats team $j$, and $n_{i j}$ to be the number of games between them, an entire season of MLB can be described with the following density:
$$
p(V \mid \pi)=\prod_{i=1}^{N-1} \prod_{j=i+1}^N\left(\begin{array}{l}
n_{i j} \
V_{i j}
\end{array}\right)\left(\frac{\pi_i}{\pi_i+\pi_j}\right)^{V_{i j}}\left(\frac{\pi_j}{\pi_i+\pi_j}\right)^{V_{j i}}
$$
Team $i$ ‘s victories against team $j$ follows a binomial distribution governed by the Bradley-Terry probability with the given strength parameters.

Rather than work with the $\pi_i$, we will transform the model by letting $\lambda_i=\log \pi_i$ for all $i$. Thus the probability $i$ defeats $j$ is
$$
\operatorname{Pr}(\text { team } i \text { defeats team } j)=\frac{\exp \left(\lambda_i\right)}{\exp \left(\lambda_i\right)+\exp \left(\lambda_j\right)}
$$

The advantage of this parameterization is that the $\lambda_i$ are unconstrained real-valued parameters.
We now carry out a Bayesian analysis of the Bradley-Terry model. We will assume a hierarchical normal prior distribution on the $\lambda_i$, that is
$$
\lambda_i \sim N(0, \sigma)
$$
for all $i=1, \ldots, N$. We will also assume that the standard deviation $\sigma$ has a uniform prior distribution,
$$
\sigma \sim \operatorname{Uniform}(0,50)
$$
with a maximum value of 50 .
Thus the full model is:
Prior distribution:
$\lambda_i \mid \sigma \sim N(0, \sigma)$, with $\sigma \sim \operatorname{Uniform}(0,50)$
Model for data:
$$
V_{i j} \mid \lambda_i, \lambda_j, n_{i j} \sim \operatorname{Binomial}\left(n_{i j}, \frac{\exp \left(\lambda_i\right)}{\exp \left(\lambda_i\right)+\exp \left(\lambda_j\right)}\right)
$$
(a) Why does this prior distribution on the $\lambda_i$ and $\sigma$ make sense? Briefly explain.
(b) Implement the model in Stan.

(c) Report the posterior means for each team’s exponentiated strength parameters (that is, $\left.\exp \left(\lambda_i\right)\right)$
(d) Using the posterior predictive distribution for the strengths of the Dodgers and Astros, simulate 1000 recreations of the 2017 World Series. That is, simulate 1000 separate series between the teams, where the series ends when either team gets to 4 wins. Based on your simulation, what was the probability that the Astros would have won the World Series last year?