MY-ASSIGNMENTEXPERT™可以为您提供my.uq.edu.au MATH2400 Mathematical Analysis数学分析的代写代考和辅导服务!
这是昆士兰大学 数学分析课程的代写成功案例。

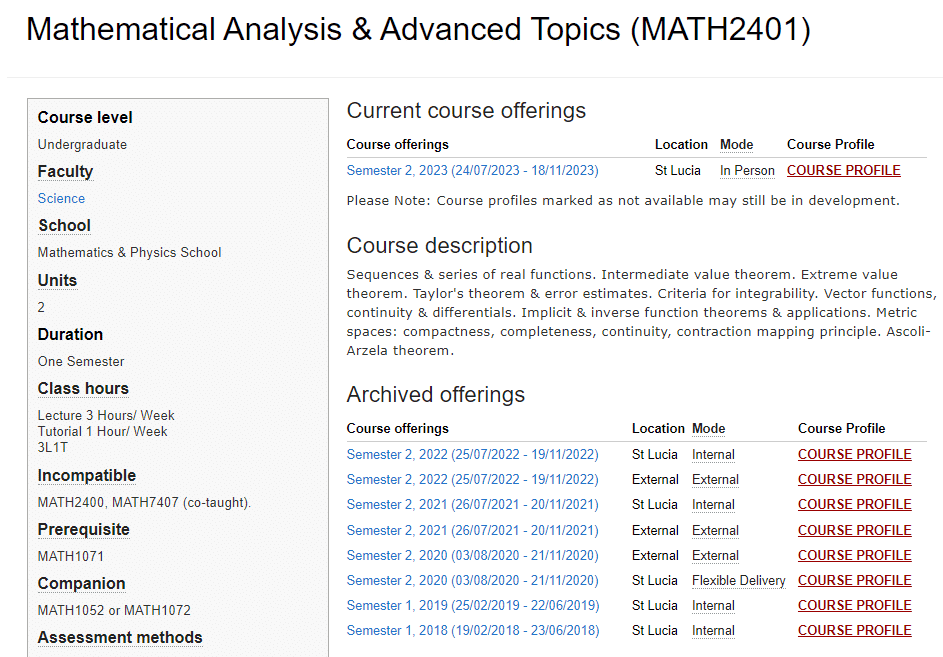
MATH2400课程简介
Course Description: (Note: MATH1052 may be taken concurrently with MATH2400 by students who only took MATH1050 & MATH1051 in 1st year.) Bounded & monotone sequences. Sequences & series of real functions. Intermediate & mean value theorems, iterative procedures. Taylor’s Theorem & error estimates. Criteria for integrability. Vector functions, continuity & differentials. Implicit & Inverse Function Theorems & applications.
Assumed Background:
MATH1051, MATH1701, or have an equivalent qualification.
Prerequisites
The course is a concise and rigurous introduction to the central concept in mathematical analysis: limits. This concept is used to develop further notions such as continuity, the differential and integral calculus of functions of single and several variables, the implicit and inverse function theorems, uniform continuity of functions and the uniform convergence of sequences of functions. By the end of this course, you will have a solid understanding of the fundamental principles of mathematical analysis and be able to use them to solve mathematical problems, rather than just mechanically applying techniques without a true understanding of their significance.
There is some overlap between this course and MATH2401. MATH2401 goes into greater depth and contains more difficult proofs.
MATH2400 Mathematical Analysis HELP(EXAM HELP, ONLINE TUTOR)
Proposition 0.1 (Exercise 1). The middle-thirds Cantor set $\mathcal{C}$ is totally disconnected and perfect.
Proof. First we show that $\mathcal{C}$ is totally disconnected. Let $x, y \in \mathcal{C}$ such that $x \neq y$. Then $|x-y|>0$, so there exists $k \in \mathbb{N}$ such that $(1 / 3)^k<|x-y|$ (because $\left.\lim _k(1 / 3)^k=0\right)$. Since $(1 / 3)^k<|x-y|, x$ and $y$ must be in different subintervals of $C_k$, since the length of each interval in $C_k$ is $(1 / 3)^k$. Thus there is a whole interval of points in $[0,1] \backslash \mathcal{C}$ between $x$ and $y$, so $\mathcal{C}$ is totally disconnected.
Now we show that $\mathcal{C}$ is perfect. Let $x \in \mathcal{C}$. We will show that $x$ is not an isolated point by finding a nearby point in $\mathcal{C}$ in a ball of any radius centered at $x$. Let $r>0$, then choose $k$ large enough that $(1 / 3)^k \leq r$. Since $\mathcal{C}=\cap_j C_j$, we have $x \in C_k$. Since each subinterval of $C_k$ has length $(1 / 3)^k$ and $x$ is in one such subinterval. Let $y$ be an endpoint of that subinterval so that $x \neq y$ (there are two endpoints, so this is always possible). Then we have $x \neq y$ and $|x-y|<(1 / 3)^k<r$, so $y \in B_r(x) \cap \mathcal{C}$. Thus $x$ is not an isolated point, and hence $\mathcal{C}$ is perfect.
Proposition 0.2 (Exercise 2a). Let $\mathcal{C}$ be the middle-thirds Cantor set. Then for $x \in[0,1]$, $x \in \mathcal{C}$ if and only if $x$ has a ternary expansion
$$
x=\sum_{k=1}^{\infty} a_k 3^{-k}
$$
where $a_k \in{0,2}$ for all $k$.
Proof. First, suppose that $x \in[0,1]$ has such a ternary expansion, where each $a_k \in{0,2}$. Since $a_1 \in{0,2}$, we know that $0 \leq x \leq 1 / 3$ or $2 / 3 \leq x \leq 1$, so $x \in C_1$. More generally, we can see by induction that $a_k \in{0,2} \Longrightarrow x \in C_k$. Thus $x \in C_k$ for all $k$, so $x \in \mathcal{C}$.
Now suppose that $x \in \mathcal{C}$. We know $x$ has some ternary expansion $\sum_{k=1}^{\infty} a_k 3^{-k}$ with $a_k \in$ ${0,1,2}$ for all $k$. Consider the remaining intervals after just the first stage of construction, $[0,1 / 3] \cup[2 / 3,1]$. If $x \in[0,1 / 3)$, then $a_1=0$. If $x=1 / 3$, then $x$ also has the ternary expansion $\sum_{k=2}^{\infty} 2 / 3$. If $x \in[2 / 3,1)$, then $a_1=2$, and if $x=1$, then $x$ has the ternary expansion $\sum_{k=1}^{\infty} 2 / 3$.
By induction on the recursive construction, at the $k$ th stage, if $x$ is in the left half of a “split” interval, then $a_k=0$, except possibly at the right endpoint. But at that endpoint, $x$ has a finite ternary expansion terminating with a $1 / 3^k$ term. But this term can be rewritten as a ternary expansion involving only 0 ‘s and 2 ‘s by the following substitution:
$$
\frac{1}{3^k}=\sum_{j=k+1}^{\infty} \frac{2}{3^j}
$$
And for $x$ in the right half of a “split” interval, we get $a_k=2$, except possibly at the right endpoint. But again, if we get a ternary expansion involving a 1 at such an endpoint, it must be a finite expansion terminating in a $1 / 3^k$ term, which we can expand as above. Thus $x$ has the required ternary expansion.
Proposition 0.3 (Exercise 2b). Let $F$ be the Cantor-Lebesgue function on $\mathcal{C}$. $F$ is well defined and continuous, and $F(0)=0$, and $F(1)=1$.
Proof. First we show that $F$ is well defined. To do this, we need to show that for $x=$ $\sum_{k=1}^{\infty} a_k 3^{-k} \in \mathcal{C}$, the value of $F$ converges. By the previous proposition, we know that $x \in \mathcal{C}$ has a ternary expansion where each $a_k$ is 0 or 2 , so if we define $b_k=a_k / 2$, each $b_k$ is 0 or 1 . Then $b_k / 2^k \leq 1 / 2^k$ for each $k$. We know that the geometric series $\sum_{k=1}^{\infty} 1 / 2^k$ converges, so by the comparison test,
$$
F(x)=\sum_{k=1}^{\infty} \frac{b_k}{2^k}
$$
converges as well. Thus $F$ is well defined.
Now we show that $F$ is continuous on $\mathcal{C}$. Let $x_0 \in \mathcal{C}$. To show that $F$ is continuous at $x_0$, we will show that for $\epsilon>0$, there exists $\delta>0$ such that
$$
\left|x-x_0\right|<\delta \Longrightarrow\left|F(x)-F\left(x_0\right)\right|<\epsilon $$ Fix $\epsilon>0$. Then there exists $n \in \mathbb{N}$ such that $2^{-n-1}<\epsilon<2^{-n}$. Let $\delta=3^{-n}$. Let
$$
x=\sum_{k=1}^{\infty} a_k 3^{-k} \quad x_0=\sum_{k=1}^{\infty} c_k 3^{-k}
$$
For convenience, let $b_k=a_k-c_k$. Then
$$
\left|x-x_0\right|=\left|\sum_{k=1}^{\infty} a_k 3^{-k}-\sum_{k=1}^{\infty} c_k 3^{-k}\right|=\left|\sum_{k=1}^{\infty}\left(a_k-c_k\right) 3^{-k}\right|=\left|\sum_{k=1}^{\infty} b_k 3^{-k}\right|
$$
If $\left|x-x_0\right|<\delta=3^{-n}$, then $b_1, b_2, \ldots b_n$ are all zero. Then the first $n$ terms of $\left|F(x)-F\left(x_0\right)\right|$ are also zero:
$$
\begin{aligned}
\left|F(x)-F\left(x_0\right)\right| & =\left|\sum_{k=1}^{\infty}\left(a_k / 2\right) 2^{-k}-\sum_{k=1}^{\infty}\left(c_k / 2\right) 2^{-k}\right|=\left|\sum_{k=1}^{\infty}\left(a_k-c_k\right) 2^{-k-1}\right| \
& =\left|\sum_{k=1}^{\infty} b_k 2^{-k-1}\right|=\left|\sum_{k=n+1}^{\infty} b_k 2^{-k-1}\right| \leq 2^{-n-1}<\epsilon
\end{aligned}
$$
Thus $F$ is continuous at $x_0$.
Now we show that $F(0)=0$ and $F(1)=1$. In the ternary expansion for zero, each $a_k=0$. In the ternary expansion of 1 , each $a_k=2$. Then
$$
\begin{aligned}
& 0=\sum_{k=1}^{\infty}(0) 3^{-k} \leadsto F(0)=\sum_{k=1}^{\infty}(0) 2^{-k}=\sum_{k=1}^{\infty} 0=0 \
& 1=\sum_{k=1}^{\infty}(2) 3^{-k} \leadsto F(1)=\sum_{k=1}^{\infty}(1) 2^{-k}=\sum_{k=1}^{\infty}\left(\frac{1}{2}\right)^k=1
\end{aligned}
$$
since both are geometric series.

MY-ASSIGNMENTEXPERT™可以为您提供MY.UQ.EDU.AU MATH2400 MATHEMATICAL ANALYSIS数学分析的代写代考和辅导服务!