MY-ASSIGNMENTEXPERT™可以为您提供stanford EE276/Stats376a: Information Theory信息论课程的代写代考和辅导服务!
这是斯坦福大学信息论课程的代写成功案例。
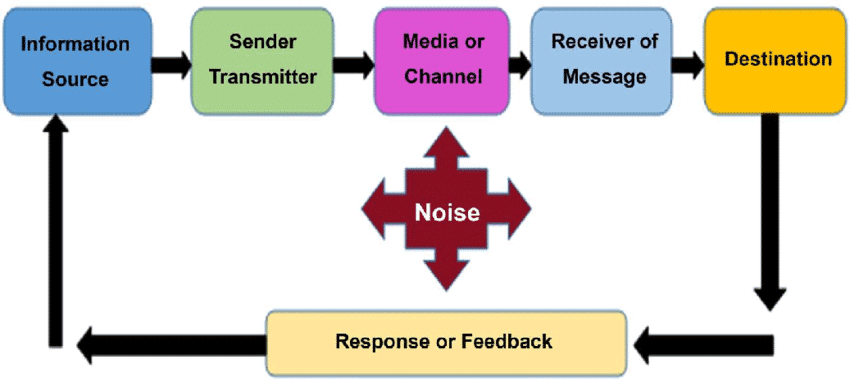
EE276/Stats376a课程简介
Information theory was invented by Claude E. Shannon in 1948 as a mathematical theory for communication but has subsequently found a broad range of applications. The first two-thirds of the course cover the core concepts of information theory, including entropy and mutual information, and how they emerge as fundamental limits of data compression and communication. The last one-third of the course focuses on applications of information theory.
Prerequisites
We will follow the following outline
0. Overview
1. Basic Concepts (1 week)
- Entropy, relative entropy, mutual information.
2. Entropy and data compression (2 weeks)
- Source entropy rate. Typical sequences and asymptotic equipartition property.
- Source coding theorem. Huffman and arithmetic codes.
- Universal compression and distribution estimation.
3. Mutual information, capacity and communication (4 weeks)
- Channel capacity. Fano’s inequality and data processing theorem.
- Jointly typical sequences. Noisy channel coding theorem.
- Achieving capacity efficiently: polar codes.
- Gaussian channels, continuous random variables and differential entropies.
- Optimality of source-channel separation.
4. Topics in Information Theory (2 weeks)
- Slepian-wolf distributed compression
- Information theoretic cryptography and common randomness
- Network coding
EE276/Stats376a: Information Theory HELP(EXAM HELP, ONLINE TUTOR)
Two fair dice are thrown. The outcome of the experiment is taken as the sum of the resulting outcomes of the two dice. What is the entropy of this experiment?
Suppose there are 3 urns, each containing two balls. The first urn contains two black balls; the second contains one black ball and one white ball; the third contains two white balls. An urn is selected at random (prob. $1 / 3$ of selecting each urn), and one ball is removed from this urn. Let $X={1,2,3}$ represent the sample space of the urn selected, and let $Y={B, W}$ be the sample space of the color ball selected. Calculate the entropies $H(X), H(Y), H(X Y), H(X \mid Y), H(Y \mid X)$, and the mutual information $I(X ; Y)$
Consider a horse race in which there are a total of 7 horses, 4 black horses and 3 grey horses; hence the sample spacce of the horse race can be represented by $X=$ $\left{b_1, b_2, b_3, b_4, g_5, g_6, g_7\right}$. Subdivide the horse race such that we have two experiments, $Y=\left{b_1, \ldots, b_4\right}$, the outcome among the black horses, and $Z=\left{g_5, \ldots, g_7\right}$ the outcome among the grey horses. Define the event $B$ as the event that a black horse wins. Assuming that in the original experiment, the a priori probabilities of any particular horse winning is equal, verify that
$$
H(X)=H(B)+P(B) H(Y)+P(\bar{B}) H(Z)
$$
Let $X$ be a random variable that only assumes non-negative integer values. Suppose $\mathrm{E}[X]=M$, where $M$ is some fixed number. In terms of $M$, how large can $H(X)$ be? Describe the extremal $X$ as completely as you can.
In class, we stated the following theorem for convex functions:
Theorem. If $\lambda_1, \ldots, \lambda_N$ are non-negative numbers whose sum is unity, then for every set of points $\left{P_1, \ldots, P_N\right}$ in the domain of the convex $\cap$ function $f(P)$, the following inequality is valid:
$$
f\left(\sum_{n=1}^N \lambda_n P_n\right) \geq \sum_{n=1}^N \lambda_n f\left(P_n\right) .
$$
Prove this theorem, and using this result, prove Jensen’s inequality:
Jensen’s Inequality. Assume $X$ is a random variable taking on values from the set $R_X=\left{x_1, \ldots, x_N\right}$ with probabilities $p_1, \ldots, p_N$. If $f(x)$ be a convex $\cap$ function whose domain includes $R_X$, then
$$
f(\mathrm{E}[X]) \geq \mathrm{E}[f(X)]
$$
Furthermore, if $f(x)$ is strictly convex, equality holds if and only if one particular element of $R_X$ is certain.
(Hint: The initial theorem is most easily proven by induction.)

MY-ASSIGNMENTEXPERT™可以为您提供STANFORD EE276/STATS376A: INFORMATION THEORY信息论课程的代写代考和辅导服务!


