MY-ASSIGNMENTEXPERT™可以为您提供manoa.hawaii MATH414 Optimization Theory最优化的代写代考和辅导服务!
这是夏威夷大学最优化的代写成功案例。

MATH414课程简介
Introduction to theory and methods for optimization. Topics may include least square analysis, search methods, conjugate direction methods, linear programming, integer programming, and constrained optimization. Pre: 243 or 253A, and 307 or 311; or consent.
Mathematical optimization (alternatively spelled optimisation) or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives.[1] It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering[2] to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries
Prerequisites
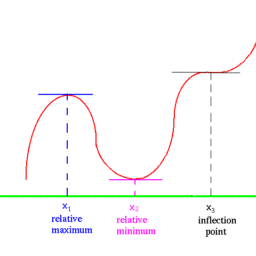
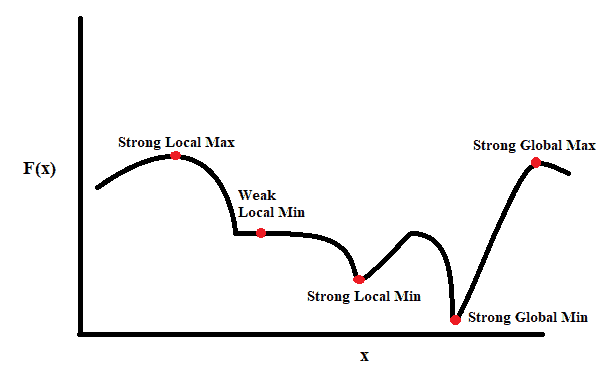
In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, optimization includes finding “best available” values of some objective function given a defined domain (or input), including a variety of different types of objective functions and different types of domains.
MATH414 Optimization Theory HELP(EXAM HELP, ONLINE TUTOR)
A manufacturer of central heating makes four models $(A, B, C$, and $D)$ of radiators. The constraints on his production are the man hours needed and the sheet steel from which the radiators are pressed. The steel is in short supply, and is delivered weekly by a regular supplier. The following data is obtained for the forthcoming week
\begin{tabular}{|l||c|c|c|c|c|}
\hline \multicolumn{1}{|c||}{} & \multicolumn{4}{c|}{ per unit of model } & \
& $\mathrm{A}$ & $\mathrm{B}$ & $\mathrm{C}$ & $\mathrm{D}$ & available \
\hline man hours & 0.5 & 1.5 & 2 & 1.5 & 500 \
steel $\left(m^2\right)$ & 4 & 2 & 6 & 8 & 2500 \
profit & 5 & 5 & 12.5 & 10 & \
\hline
\end{tabular}
Formulate the manufacturer’s production planning problem (maximization of profit) as a linear program.
4 Points
The ACME Electronics Company makes black-and-white (bw) and color television sets. Each bw set requires 3 hours of assembly, 1 hour of finishing, and 2 hours of testing. Each color set requires 5 hours of assembly, 3 hours of finishing, and 2 hours of testing. For this week’s production run, ACME has required 3900 hours of assembly, 2100 hours of finishing, and 2200 hous of testing. If a bw set and a color set bring in $\$ 100$ and $\$ 200$ profit, respectively, then how many of each set should the company produce this week in order to maximize profit, and what is the maximum achievable profit?
Set up the problem as a linear program.
4 Points
A farmer has a 1000 hectare farm on which he is considering growing barley and wheat. Land which is not sown with either crop will be left for grazing. He has sufficient cultivating and sowing machinery to sow up to 500 hectares of crop. It takes 4 hours to harvest 1 hectare of barley, but 8 hours to harvest 1 hectare of wheat. The farmer has several harvesters which are available for a total of 2800 hours in the appropriate period of the year. Barley, wheat and grazing require 30 kilos, 60 kilos, and 20 kilos of fertilizer per hectare, respectively, and yield an anuual profit of $\$ 60, \$ 100$, and $\$ 40$ per hectare, respectively. The farmer has 32000 kilos of fertilizer available. Obviously, the farmer wants to maximize his profit.
Formulate the farmer’s problem as a linear problem and specify the associated dual problem.
4 Points
This exercise is reprinted from [Strauss], §1.6, Exercise 6.
Consider the partial differential equation:
$$
3 \frac{\partial u}{\partial y}+\frac{\partial^2 u}{\partial x \partial y}=0
$$
where the unknown $u \equiv u(x, y)$ is a function of two real variables.
(1) What is the order of this PDE? What is its type?
(2) Find the general solution of this PDE. (Hint: make the change of unknown function $v:=\frac{\partial u}{\partial y}$, and solve first the corresponding PDE of the unknown function $v)$.
(3) If this equation is supplemented with the boundary conditions:
$$
\forall x \in \mathbb{R}, u(x, 0)=e^{-3 x}, \text { and } \frac{\partial u}{\partial y}(x, 0)=0 ;
$$
does it admit a solution? Is this solution unique?

MY-ASSIGNMENTEXPERT™可以为您提供MANOA.HAWAII MATH414 OPTIMIZATION THEORY最优化的代写代考和辅导服务!