MY-ASSIGNMENTEXPERT™可以为您提供stanford.edu MS&E310 Linear Programming线性规划课程的代写代考和辅导服务!
这是斯坦福大学 线性规划课程的代写成功案例。

MS&E310课程简介
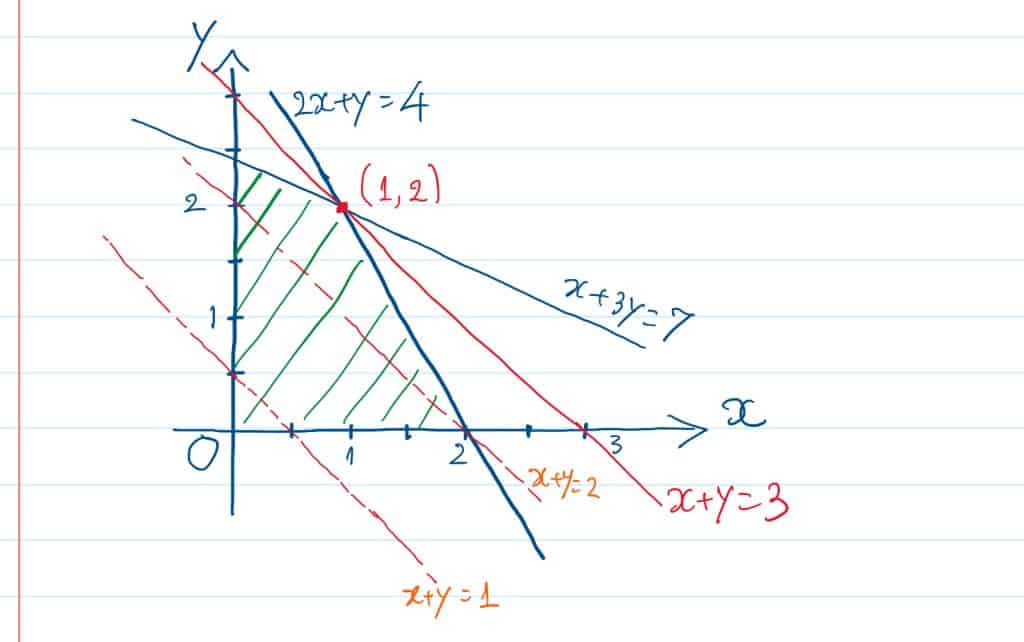
Topics include: Problem formulation of standard (conic) linear programming models, the theory of polyhedral and conic convex sets, linear inequalities, alternative theorems and duality, sensitivity analyses and economic interpretations, and relaxations of harder optimization problems. Algorithms include the simplex method, interior-point methods, and ADMM and other (first-order) iterative methods. Complexity and/or computation efficiency analysis for linear programming. Applications include dynamic resource allocation, on-line mechanism design, algorithmic game-theory, SVM/data-classification, and MDP/reinforced learning.
Prerequisites
The field of optimization is concerned with the study of maximization and minimization of mathematical functions. Very often the arguments of (i.e., variables in) these functions are subject to side conditions or constraints. By virtue of its great utility in such diverse areas as applied science, engineering, economics, finance, medicine, and statistics, optimization holds an important place in the practical world and the scientific world. Indeed, as far back as the Eighteenth Century, the famous Swiss mathematician and physicist Leonhard Euler (1707-1783) proclaimed that … nothing at all takes place in the Universe in which some rule of maximum or minimum does not appear. The subject is so pervasive that we even find some optimization terms in our everyday language.
MS&E310 Linear Programming HELP(EXAM HELP, ONLINE TUTOR)
Let $G$ be a graph with distinct, positive edge weights $c(e)$ on every edge $e$. Show that if $T$ is a minimum spanning tree of $G$, then $T$ is a minimum spanning tree of $G^{\prime}$ where $G^{\prime}$ is the same as $G$ except it has $\operatorname{costs} c^{\prime}(e)=c(e)^2$ on every edge (the cost of every edge is squared).
Let $G$ be a graph that represents a computer network, and let $b(e)$ be the bottleneck of edge $e$ assume all edges have distinct, positive bottlenecks. When two nodes $u$ and $v$ want to communicate over a path $P$, the rate at which they can communicate is the minimum bottleneck along that path: $b(P)=\min _{e \in P} b(e)$. The best path $B(u, v)$ between two nodes $u$ and $v$ is the path $P$ that maximizes $b(P)$ (i.e. has the largest, smallest bottleneck).
It turns out there is a single spanning tree $T$ such that for every pair of nodes $u$ and $v$, a best path $B(u, v)$ for them is contained in the tree $T$. That is, a single tree can encode best paths between every pair of nodes.
Give an efficient algorithm to find such a tree $T$ and argue why your algorithm is correct.
Rank the following functions in order of their asymptotic growth. That is if $f_i(n)=O\left(f_j(n)\right)$ then $f_i(n)$ should come before $f_j(n)$ in your list. If $f_i(n)=\Theta\left(f_j(n)\right)$ then the two functions should be given the same rank.
- $f_1(n)=n^3$
- $f_2(n)=n$ !
- $f_3(n)=n \log _2 n$
- $f_4(n)=1$
- $f_5(n)=2^{\log _2 n}$
- $f_6(n)=10 n \log _{10} n$
- $f_7(n)=(n+1)$ !
- $f_8(n)=2^{\log _{50} n}$
- $f_9(n)=4^{\log _2 n}$
- $f_{10}(n)=n^{\log _2 \log _2 n}$
Let $f(n)$ and $g(n)$ be functions that take on positive values for all $n>1$ and such that $f(n)=O(g(n))$. Prove or give a counterexample to the following statements:
(a) $2^{n+1}=O\left(2^n\right)$
(b) $2^{2 n}=O\left(2^n\right)$
(c) $3^n=O\left(2^n\right)$
(d) $f(n)=\Theta(f(n / 2))$
(e) $f(n)=O(g(n))$ implies $g(n)=\Omega(f(n))$
(f) $\log _2 f(n)=O\left(\log _2 g(n)\right)$
(g) $2^{f(n)}=O\left(2^{g(n)}\right)$
(h) $f(n)^2=O\left(g(n)^2\right)$

MY-ASSIGNMENTEXPERT™可以为您提供STANFORD.EDU MS&E310 LINEAR PROGRAMMING线性规划课程的代写代考和辅导服务!