MY-ASSIGNMENTEXPERT™可以为您提供cornell.edu Physics6561 Electrodynamics电动力学课程的代写代考和辅导服务!
这是康乃尔大学电动力学课程的代写成功案例。
Physics6561课程简介
As an undergraduate you learn the language of physics, the laws of physics, and even some physics trivia. And thanks to the skill of your instructors, the subject hums like a well oiled machine. If there’s anything that’s daunting, occasionally, it’s some of the math that comes with the territory. But that’s incidental since you know that, fundamentally, physics is simple and elegant.
But by the time you’re a graduate student you realize that the world doesn’t always seem to play by the rules of the physics laid out in textbooks. There are subtleties, apparent contradictions, paradoxes. You find out that eventually these things got resolved, but when they first appeared on the radar they were called effects. Coming to terms with the effects of physics is a good way to think of the next phase of your education.
Prerequisites
No doubt some effects, such as Aharonov-Bohm, came up in undergraduate physics. The best effects, such as this one, increase your understanding in a deep way, like the vector potential is a more fundamental description of the electromagnetic field. While not all effects are this famous, every one of them provided an important lesson in physics at some point in time. In fact, the name of the effect often becomes a proxy for a general concept, as for example Hanbury-Brown and Twiss effect might be used to describe an experiment involving electrons when in fact the original effect arose in stellar interferometry.
Physics6561 Electrodynamics HELP(EXAM HELP, ONLINE TUTOR)
Wire with a Linearly Rising Current
A neutral wire along the $z$-axis carries current $I$ that varies with time $t$ according to
$$
I(t)= \begin{cases}0 & (t \leq 0), \ \alpha t & (t>0), \quad \alpha \text { is a constant. }\end{cases}
$$
Deduce the time-dependence of the electric and magnetic fields, $\mathbf{E}$ and $\mathbf{B}$, observed at a point $(r, \theta=0, z=0)$ in a cylindrical coordinate system about the wire. Use your expressions to discuss the fields in the two limiting cases that $c t \gg r$ and $c t=r+\epsilon$, where $c$ is the speed of light and $\epsilon \ll r$.
Harmonic Multipole Expansion
A common alternative to the multipole expansion of electromagnetic radiation given in the Notes assumes from the beginning that the motion of the charges is oscillatory with angular frequency $\omega$. However, we still use the essence of the Hertz method wherein the current density is related to the time derivative of a polarization: ${ }^1$
$$
\mathbf{J}=\dot{\mathbf{p}}
$$
The radiation fields will be deduced from the retarded vector potential,
$$
\mathbf{A}=\frac{1}{c} \int \frac{[\mathbf{J}]}{r} d \mathrm{Vol}=\frac{1}{c} \int \frac{[\dot{\mathbf{p}}]}{r} d \mathrm{Vol},
$$
which is a solution of the (Lorenz gauge) wave equation
$$
\nabla^2 \mathbf{A}-\frac{1}{c^2} \frac{\partial^2 \mathbf{A}}{\partial t^2}=-\frac{4 \pi}{c} \mathbf{J}
$$
Suppose that the Hertz polarization vector $\mathbf{p}$ has oscillatory time dependence,
$$
\mathbf{p}(\mathbf{x}, t)=\mathbf{p}_\omega(\mathbf{x}) e^{-i \omega t}
$$
Using the expansion
$$
r=R-\mathbf{r}^{\prime} \cdot \hat{\mathbf{n}}+\ldots
$$
of the distance $r$ from source to observer,
show that
$$
\mathbf{A}=-i \omega \frac{e^{i(k R-\omega t)}}{c R} \int \mathbf{p}\omega\left(\mathbf{r}^{\prime}\right)\left(1+\mathbf{r}^{\prime} \cdot \hat{\mathbf{n}}\left(\frac{1}{R}-i k\right)+\ldots\right) d \mathrm{Vol}^{\prime} $$ where no assumption is made that $R \gg$ source size or that $R \gg \lambda=2 \pi / k=2 \pi c / \omega$. Consider now only the leading term in this expansion, which corresponds to electric dipole radiation. Introducing the total electric dipole moment, $$ \mathbf{P} \equiv \int \mathbf{p}\omega\left(\mathbf{r}^{\prime}\right) d \mathrm{Vol}^{\prime},
$$
use
$$
\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A} \quad \text { and } \quad \boldsymbol{\nabla} \times \mathbf{B}=\frac{1}{c} \frac{\partial \mathbf{E}}{\partial t}
$$
to show that for an observer in vacuum the electric dipole radiation fields are
$$
\begin{gathered}
\mathbf{B}=k^2 \frac{e^{i(k R-\omega t)}}{R}\left(1+\frac{i}{k R}\right) \hat{\mathbf{n}} \times \mathbf{P}, \
\mathbf{E}=k^2 \frac{e^{i(k R-\omega t)}}{R}\left{\hat{\mathbf{n}} \times(\mathbf{P} \times \hat{\mathbf{n}})+[3(\hat{\mathbf{n}} \cdot \mathbf{P}) \hat{\mathbf{n}}-\mathbf{P}]\left(\frac{1}{k^2 R^2}-\frac{i}{k R}\right)\right} .
\end{gathered}
$$
Alternatively, deduce the electric field from both the scalar and vector potentials via
$$
\mathbf{E}=-\boldsymbol{\nabla} \phi-\frac{1}{c} \frac{\partial \mathbf{A}}{\partial t}
$$
in both the Lorenz and Coulomb gauges.
For large $R$,
$$
\mathbf{B}{\mathrm{far}} \approx k^2 \frac{e^{i(k R-\omega t)}}{R} \hat{\mathbf{n}} \times \mathbf{P}, \quad \mathbf{E}{\mathrm{far}} \approx \mathbf{B}{\mathrm{far}} \times \hat{\mathbf{n}} $$ while for small $R$, $$ \mathbf{B}{\text {near }} \approx \frac{i k}{R^2}(\hat{\mathbf{n}} \times \mathbf{P}) e^{-i \omega t}, \quad \mathbf{E}{\text {near }} \approx \frac{3(\hat{\mathbf{n}} \cdot \mathbf{P}) \hat{\mathbf{n}}-\mathbf{P}}{R^3} e^{-i \omega t}, $$ Thus, $B{\text {near }} \ll E_{\text {near }}$, and the electric field $\mathbf{E}_{\text {near }}$ has the shape of the static dipole field of moment $\mathbf{P}$, modulated at frequency $\omega$.
Calculate the Poynting vector of the fields of a Hertzian oscillating electric dipole (10)(11) at all points in space. Show that the time-averaged Poynting vector has the same form in the near zone as it does in the far zone, which confirms that (classical) radiation exists both close to and far from the source.
Extend your discussion to the case of an oscillating, point magnetic dipole by noting that if $\mathbf{E}(\mathbf{r}, t)$ and $\mathbf{B}(\mathbf{r}, t)$ are solutions to Maxwell’s equations in free space (i.e., where the charge density $\rho$ and current density $\mathbf{J}$ are zero), then the dual fields
$$
\mathbf{E}^{\prime}(\mathbf{r}, t)=-\mathbf{B}(\mathbf{r}, t), \quad \mathbf{B}^{\prime}(\mathbf{r}, t)=\mathbf{E}(\mathbf{r}, t)
$$
are solutions also.
An electric dipole of moment $p_0$ lies in the $x-y$ plane and rotates about the $x$ axis with angular velocity $\omega$.
Calculate the radiation fields and the radiated power according to an observer at angle $\theta$ to the $z$ axis in the $x-z$ plane.
Define $\hat{\mathbf{n}}$ towards the observer, so that $\hat{\mathbf{n}} \cdot \hat{\mathbf{z}}=\cos \theta$, and let $\hat{\mathbf{l}}=\hat{\mathbf{y}} \times \hat{\mathbf{n}}$.
Show that
$$
\mathbf{B}{\mathrm{rad}}=p_0 k^2 \frac{e^{i(k r-\omega t)}}{r}(\cos \theta \hat{\mathbf{y}}-i \hat{\mathbf{l}}), \quad \mathbf{E}{\mathrm{rad}}=p_0 k^2 \frac{e^{i(k r-\omega t)}}{r}(\cos \theta \hat{\mathbf{1}}+i \hat{\mathbf{y}}),
$$
where $r$ is the distance from the center of the dipole to the observer.
Note that for an observer in the $x-y$ plane $(\hat{\mathbf{n}}=\hat{\mathbf{x}})$, the radiation is linearly polarized, while for an observer along the $z$ axis it is circularly polarized.
Show that the (time-averaged) radiated power is given by
$$
\frac{d\langle P\rangle}{d \Omega}=\frac{c}{8 \pi} p_0^2 k^4\left(1+\cos ^2 \theta\right), \quad\langle P\rangle=\frac{2 c p_0^2 k^4}{3}=\frac{2 p_0^2 \omega^4}{3 c^3}
$$
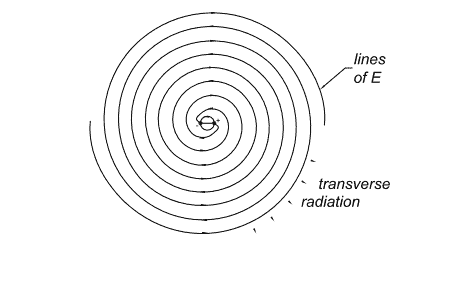
This example gives another simple picture of how radiation fields are generated. The field lines emanating from the dipole become twisted into spirals as the dipole rotates. At large distances, the field lines are transverse…
Magnetars
The x-ray pulsar SGR1806-20 has recently been observed to have a period $T$ of $7.5 \mathrm{~s}$ and a relatively large “spindown” rate $|\dot{T}|=8 \times 10^{-11}$. See, C. Kouveliotou et al., An $X$-ray pulsar with a superstrong magnetic field in the soft $\gamma$-ray repeater SGR1806-20, Nature 393, 235-237 (1998). ${ }^2$
Calculate the maximum magnetic field at the surface of this pulsar, assuming it to be a standard neutron star of mass $1.4 M_{\odot}=2.8 \times 10^{30} \mathrm{~kg}$ and radius $10 \mathrm{~km}$, that the mass density is uniform, that the spindown is due to electromagnetic radiation, and that the angular velocity vector is perpendicular to the magnetic dipole moment of the pulsar.
Compare the surface magnetic field strength to the so-called QED critical field strength $m^2 c^3 / e \hbar=4.4 \times 10^{13}$ gauss, at which electron-positron pair creation processes become highly probable.

MY-ASSIGNMENTEXPERT™可以为您提供CORNELL.EDU PHYSICS6561 ELECTRODYNAMICS电动力学课程的代写代考和辅导服务!