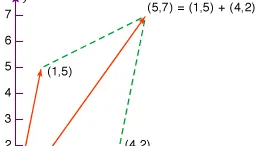
MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH1002 Linear Algebra线性代数的代写代考和辅导服务!
这是悉尼大学线性代数课程的代写成功案例。
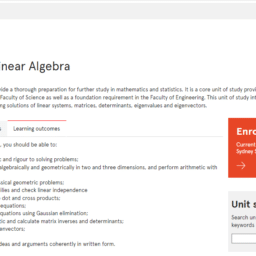
MATH1002课程简介
MATH1002 is designed to provide a thorough preparation for further study in mathematics and statistics. It is a core unit of study providing three of the twelve credit points required by the Faculty of Science as well as a foundation requirement in the Faculty of Engineering. This unit of study introduces vectors and vector algebra, linear algebra including solutions of linear systems, matrices, determinants, eigenvalues and eigenvectors.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. apply mathematical logic and rigour to solving problems;
- LO2. represent vectors both algebraically and geometrically in two and three dimensions, and perform arithmetic with them;
- LO3. use vectors to solve classical geometric problems;
- LO4. determine spanning families and check linear independence
- LO5. perform and manipulate dot and cross products;
- LO6. set up systems of linear equations;
- LO7. solve systems of linear equations using Gaussian elimination;
- LO8. perform matrix arithmetic and calculate matrix inverses and determinants;
- LO9. find eigenvalues and eigenvectors;
- LO10. diagonalise a matrix;
- LO11. express mathematical ideas and arguments coherently in written form.
MATH1002 Linear algebra HELP(EXAM HELP, ONLINE TUTOR)
Consider Example 1.3 section 1.1, where we had to solve the following linear system:
$$
\begin{aligned}
x+2 y+4 z & =7 \
3 x+7 y+2 z & =-11 \
2 x+3 y+3 z & =1
\end{aligned}
$$
Write the augmented matrix of this linear system.
Solution
An augmented matrix is simply a shorthand way of representing a linear system of equations. Rather than write $x, y$ and $z$ after each coefficient, recognize that the first column contains the coefficients of $x$, the second column the coefficients of $y$ and so on. Placing the coefficients of $x, y$ and $z$ on the left hand side of the vertical line in the augmented matrix and the constant values $7,-11$ and 1 on the right hand side we have
$$
\left(\begin{array}{lll|r}
1 & 2 & 4 & 7 \
3 & 7 & 2 & -11 \
2 & 3 & 3 & 1
\end{array}\right)
$$
Solve the following linear system by using the Gaussian elimination procedure:
$$
\begin{aligned}
& x-3 y+5 z=-9 \
& 2 x-y-3 z=19 \
& 3 x+y+4 z=-13
\end{aligned}
$$
Solution
What is the augmented matrix in this case?
Let $R_1, R_2$ and $R_3$ represent rows 1,2 and 3 respectively. We have
Note that each row represents an equation.
How can we find the unknowns $x, y$ and $z$ ?
The columns in the matrix represent the $x, y$ and $z$ coefficients respectively. If we can transform this augmented matrix into
$$
\begin{aligned}
& \begin{array}{lll}
x & y & z
\end{array} \
& \downarrow \downarrow \downarrow \
&
\end{aligned}
$$
Final row $\left(\begin{array}{ccc|c}* & * & * & * \ 0 & * & * & * \ 0 & 0 & A & B\end{array}\right)$ where $A, B$ and * represents any real number then we can find $z$.
How?
Look at the final row.
What does this represent?
$$
(0 \times x)+(0 \times y)+(A \times z)=B
$$
$$
A z=B \text { which gives } z=\frac{B}{A} \text { provided } A \neq 0
$$
Hence we have a value for $z=B / A$.
But how do we find the other two unknowns $x$ and $y$ ?
Now we can use a method called back substitution. Examine the second row of the above matrix:
$$
\text { Second row }\left(\begin{array}{ccc|c}
x & y & z & \
& * & * & * \
0 & * & * & * \
0 & 0 & A & B
\end{array}\right)
$$
By expanding the second row we get an equation in terms of $y$ and $z$. From above we already know the value of $z=B / A$, so we can substitute $z=B / A$ and obtain $y$. Similarly from the first row we can find $x$ by substituting the values of $y$ and $z$.
Solve the linear system:
$$
\begin{aligned}
x+3 y+2 z & =13 \
4 x+4 y-3 z & =3 \
5 x+y+2 z & =13
\end{aligned}
$$
Solution
How can we find the unknowns $x, y$ and $z$ ?
We use Gaussian elimination with back substitution.
The augmented matrix is:
Our aim is to convert this augmented matrix so that there are 0’s in the bottom left hand corner, that is; the first 4 in the second row reduces to zero, and the 5 and 1 from the bottom row reduce to zero. Hence $4 \rightarrow 0,5 \rightarrow 0$ and $1 \rightarrow 0$.
To get 0 in place of the first 4 in the middle row we multiply row $1, R_1$, by 4 and take the result away from row $2, R_2$, that is $R_2-4 R_1$. To get 0 in place of 5 in the bottom row we multiply row $1, R_1$, by 5 and take the result away from row $3, R_3$, that is $R_3-5 R_1$. Combining the two row operations, $R_2-4 R_1$ and $R_3-5 R_1$, we have
$$
\begin{gathered}
\mathrm{R}_1 \
\mathrm{R}_2^{\dagger}=\mathrm{R}_2-4 \mathrm{R}_1 \
\mathrm{R}_3^{\dagger}=\mathrm{R}_3-5 \mathrm{R}_1
\end{gathered}\left(\begin{array}{ccc|c}
1 & 3 & 2 & 13 \
4-(4 \times 1) & 4-(4 \times 3) & -3-(4 \times 2) & 3-(4 \times 13) \
5-(5 \times 1) & 1-(5 \times 3) & 2-(5 \times 2) & 13-(5 \times 13)
\end{array}\right)
$$
We call the new row 2 and $3-\mathrm{R}_2^{\dagger}$ and $\mathrm{R}_3^{\dagger}$ respectively. This simplifies to:
\begin{aligned}
& \mathrm{R}_1 \
& \mathrm{R}_2^{\dagger} \
& \mathrm{R}_3^{\dagger}
\end{aligned}\left(\begin{array}{rrr|r}
1 & 3 & 2 & 13 \
0 & -8 & -11 & -49 \
0 & -14 & -8 & -52
\end{array}\right)
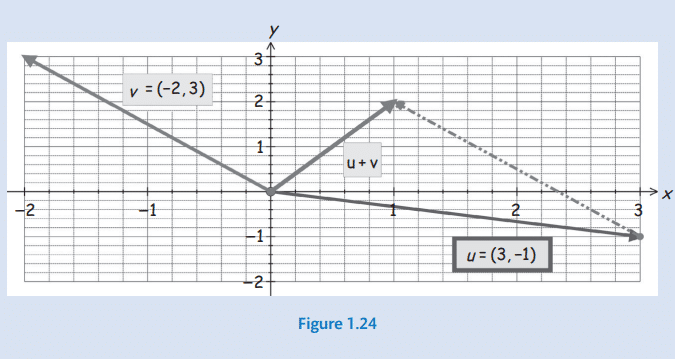
Let $\mathbf{u}=\left(\begin{array}{r}3 \ -1\end{array}\right)$ and $\mathbf{v}=\left(\begin{array}{r}-2 \ 3\end{array}\right)$. Plot $\mathbf{u}+\mathbf{v}$ and write down $\mathbf{u}+\mathbf{v}$ as a column vector.
By examining Fig. 1.24 we see that the coordinates of $\mathbf{u}+\mathbf{v}$ are $(1,2)$ and this is written as a column vector $\left(\begin{array}{l}1 \ 2\end{array}\right)$.
What do you notice about your result?
If we add $x$ and $y$ coordinates in the vectors separately then we obtain the resultant vector.
That is, we evaluate $\mathbf{u}+\mathbf{v}=\left(\begin{array}{r}3 \ -1\end{array}\right)+\left(\begin{array}{r}-2 \ 3\end{array}\right)=\left(\begin{array}{r}3-2 \ -1+3\end{array}\right)=\left(\begin{array}{l}1 \ 2\end{array}\right)$, which means that we can simply add the corresponding entries of the vector to find $\mathbf{u}+\mathbf{v}$.

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY MATH1002 LINEAR ALGEBRA线性代数的代写代考和辅导服务!