MY-ASSIGNMENTEXPERT™可以为您提供ntnu.edu TEP4120 Thermodynamics热力学课程的代写代考和辅导服务!
这是挪威科技大学 热力学课程的代写成功案例。
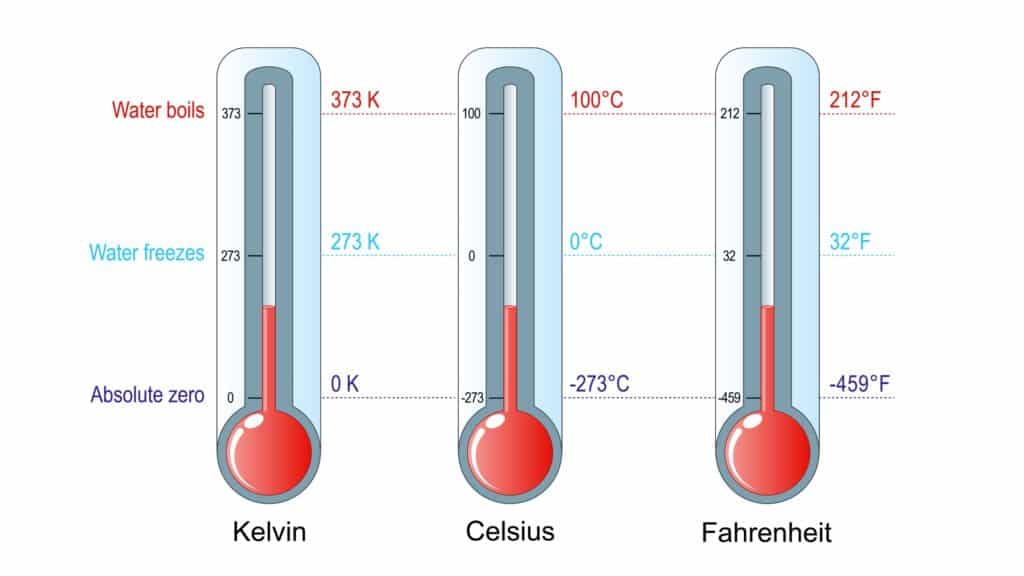
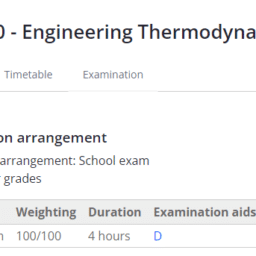
TEP4120课程简介
Course content
Concepts and definitions; the thermodynamic system, properties, phase equilibrium of pure substances, equations of state for gases, tables of thermodynamic properties, work and heat. First law of thermodynamics; thermodynamic cycles, change of state, internal energy, enthalpy, specific heat; open systems, steady-state and transient processes. Second law of thermodynamics; reversible and irreversible processes, the Carnot cycle, the thermodynamic temperature scale, entropy, the entropy production concept. Thermodynamic power cycles, refrigeration cycles, the Otto cycle and the Diesel cycle, the gas-turbine process. Introduction to exergy analysis.
Prerequisites
LKnowledge: The course provides the student with knowledge about: – Conservation laws for mass and energy (including the 1st law of Thermodynamics). – Forms of energy such as work (power) and heat, internal energy and enthalpy. – Entropy and the 2nd law of thermodynamics. – Reasons for thermodynamic losses in the form of irreversibilities. – The quality of different forms of energy measured as the ability to produce work. – Destruction of energy quality in processes. – Ideal gas model, its assumptions, applications and limitations. – Different cyclic processes such as Carnot, Rankine, Otto, Diesel and Brayton. The course gives the student insight about: – Operation of steam and gas based power stations, internal combustion engines, heat pumps and refrigeration cycles. – The main components of heat & power processes, such as steam and gas turbines, compressors, pumps, fans, heat exchangers and valves. – The ability of fluids to change phase (solid, liquid and gas).
TEP4120 Thermodynamics HELP(EXAM HELP, ONLINE TUTOR)
Entropy and Temperature
Suppose the number of states of energy $U$ is given by $g(U)=C U^{3 N / 2}$, where $C$ is a constant and $N$ is the number of particles.
(a) Show that $U=\frac{3}{2} N k_B T$.
(b) Show that $\left(\partial^2 S / \partial U^2\right)_N$ is negative.
Note: This expression for $g(U)$ actually applies to a classical ideal gas.
(a) From $g(U)=C U^{3 N / 2}$ we have, with $S=k_B \ln g$,
$$
\frac{1}{T}=\left(\frac{\partial S}{\partial U}\right)_N=k_B \frac{3 N}{2} \frac{1}{U},
$$
and hence
$$
U=\frac{3}{2} N k_B T .
$$
This is the form of the energy of an ideal gas, as we will discuss later in the course.
(b) Differentiating Eq. (1) again gives
$$
\left(\frac{\partial^2 S}{\partial U^2}\right)_N=-k_B \frac{3 N}{2} \frac{1}{U^2},
$$
which is negative.
Paramagnetism
Consider the toy model of $N$ non-interacting “Ising” spins in a magnetic file $B$, discussed in class. Each spin has a magnetic moment $\mu_i=\mu S_i$, where $S_i$ takes values \pm 1 . The total magnetization, $M$, is equal to $\sum_i \mu_i$, and the difference between the number of up spins and the number of down spins, i.e. $\sum_i S_i$, is equal to $2 l$. The energy is given by
$$
U=-M B=-B \sum_i \mu_i=-2 \mu l B
$$
Take the entropy, the logarithm of the multiplicity, to be that given in the book
$$
\frac{S}{k_B}=\sigma(l) \simeq \log g(N, 0)-2 l^2 / N,
$$
for $l \ll N$.
Using the result that the temperature is given by $1 / T=(\partial S / \partial U)N$, find the magnetization per spin $m$, where $$ m \equiv \frac{M}{N}=\frac{1}{N} \sum{i=1}^N \mu_i
$$
as a function of $T$ and $B$.
Note: The result you obtain, which is known as Curie’s law, will be rederived later in the course in a simpler way which does not involve the multiplicity function.
We are given that
$$
\sigma(l) \simeq \ln g(N, 0)-\frac{2 l^2}{N},
$$
and we also know that
$$
U=-2 l \mu B \quad(=-M B),
$$
so
$$
\sigma(U) \simeq \ln g(N, 0)-\frac{U^2}{2 \mu^2 B^2 N} .
$$
Differentiating with respect to $U$ gives
$$
\frac{1}{T}=k_B\left(\frac{\partial \sigma}{\partial U}\right)_N=-k_B \frac{U}{N \mu^2 B^2} .
$$
Rearranging gives
$$
U=-\frac{N \mu^2 B^2}{k_B T}
$$
and hence, from Eq. (2), the magnetization per site, $m \equiv M / N$, is given by
$$
m=\frac{\mu^2 B}{k_B T}
$$
Note: We shall derive this result, which is known as Curie’s law, by an easier method later in the class.
Quantum Harmonic Oscillator Consider a set of $N$ oscillators of frequency $\omega$. Assume that the total quantum number is fixed to be $n$, i.e.
$$
n_1+n_2+\cdots+n_N=n .
$$
The multiplicity function, i.e. the number of (ordered) ways in which $N$ non-negative integers can add up to $n$, is given by
$$
g(N, n)=\frac{1}{n !} N(N+1)+\cdots(N+n-1)=\frac{(N+n-1) !}{n !(N-1) !} .
$$
This result is not obvious but a derivation is given in Kittel and Kroemer p. 25.
(a) Using this expression for $g$, determine the entropy of the oscillators assuming $N$ and $n$ are large (so you can use Stirling’s approximation $\log N ! \simeq N \log N-N$, and also replace $N-1$ by $N)$.
(b) Let $U$ denote the total energy $n \hbar \omega$ of the oscillators. Express the entropy as $S(U, N)$. Using $1 / T=(\partial S / \partial U)_N$ show that the total energy at temperature $T$ is
$$
U=N \frac{\hbar \omega}{\exp \left(\hbar \omega / k_B T\right)-1} .
$$
Note: This is the Planck result which we will rederive later in the course by a more powerful method which is much simpler because it does not require us to find the multiplicity function.
(a) If the energy of the $i$-th oscillator is $\left(n_i+1 / 2\right) \hbar \omega$, then the constraint given in the question is
$$
n_1+n_2+\cdots+n_N=n,
$$
where $n$ is fixed. The number of ways of dividing up the energy among the oscillators is given by (see Eq. (1.55) of Kittel and Kroemer)
$$
g=\frac{(N+n-1) !}{n !(N-1) !}
$$
Taking logs, using Stirling’s approximation $\ln N ! \simeq N \ln N-N$, and replacing $N-1$ by $N$, the entropy $\sigma \equiv \ln g$ is given by
$$
\sigma=(N+n) \ln (N+n)-N \ln N-n \ln n .
$$
(b) Writing $n=U /(\hbar \omega)$ and differentiating with respect to $U$ gives
$$
\frac{1}{T}=\left(\frac{\partial S}{\partial U}\right)_N=k_B\left(\frac{\partial \sigma}{\partial U}\right)_N=k_B \frac{1}{\hbar \omega}[\ln (N+n)-\ln n]=k_B \frac{1}{\hbar \omega} \ln \left(\frac{1+n / N}{n / N}\right) .
$$
This gives
$$
\frac{n}{N}\left(\equiv \frac{U}{N \hbar \omega}\right)=\frac{1}{\exp \left(\hbar \omega / k_B T\right)-1} .
$$
Note: This is called the Planck distribution.
MY-ASSIGNMENTEXPERT™可以为您提供CATALOG.WINONA.EDU PHYS451 QUANTUM MECHANICS量子力学课程的代写代考和辅导服务