MY-ASSIGNMENTEXPERT™可以为您提供ntnu.edu TEP4120 Thermodynamics热力学课程的代写代考和辅导服务!
这是挪威科技大学 热力学课程的代写成功案例。
TEP4120课程简介
Course content
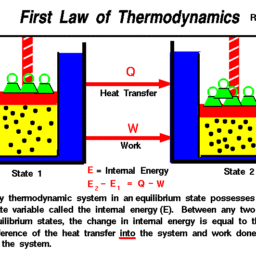
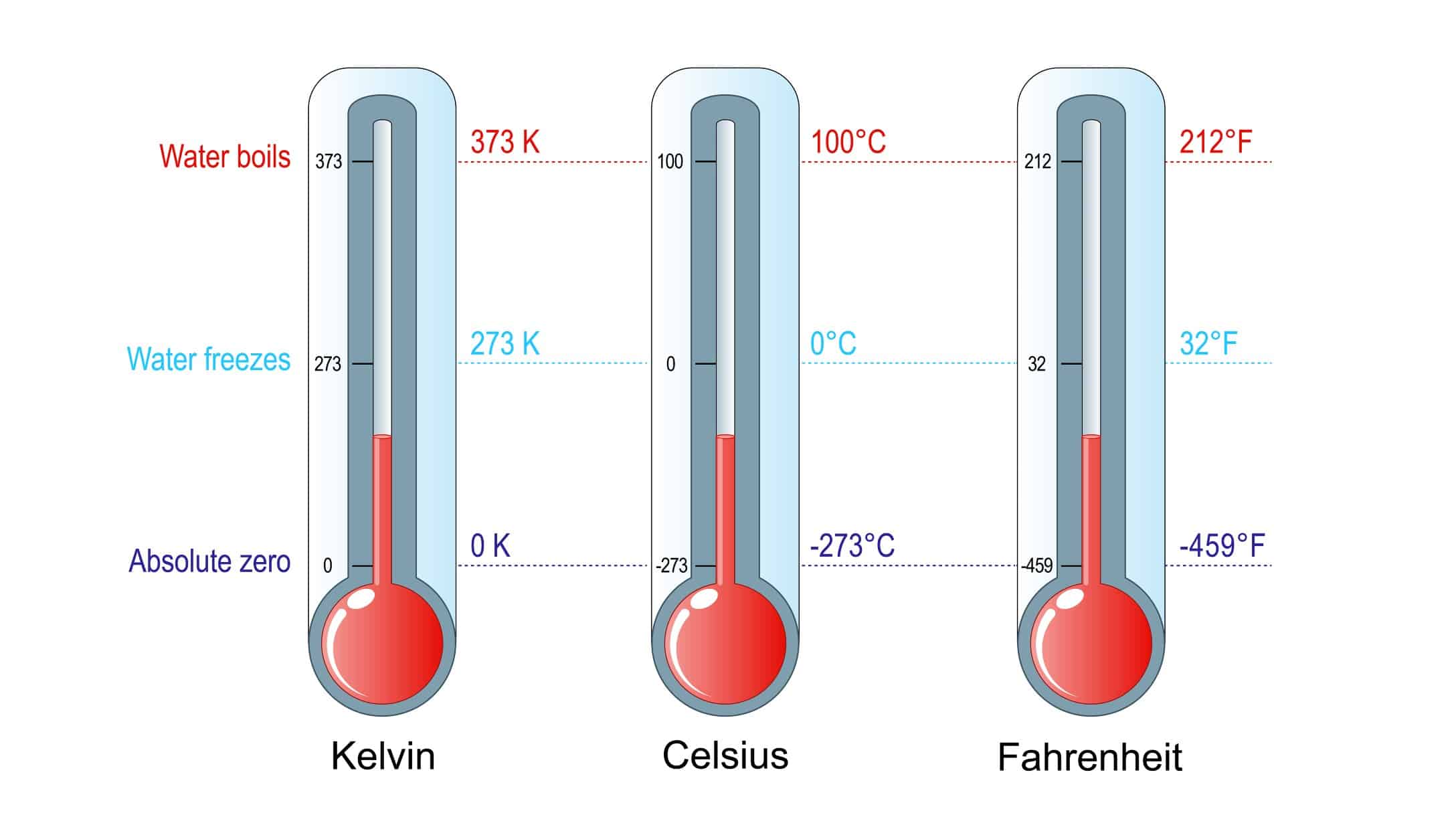
Concepts and definitions; the thermodynamic system, properties, phase equilibrium of pure substances, equations of state for gases, tables of thermodynamic properties, work and heat. First law of thermodynamics; thermodynamic cycles, change of state, internal energy, enthalpy, specific heat; open systems, steady-state and transient processes. Second law of thermodynamics; reversible and irreversible processes, the Carnot cycle, the thermodynamic temperature scale, entropy, the entropy production concept. Thermodynamic power cycles, refrigeration cycles, the Otto cycle and the Diesel cycle, the gas-turbine process. Introduction to exergy analysis.
Prerequisites
LKnowledge: The course provides the student with knowledge about: – Conservation laws for mass and energy (including the 1st law of Thermodynamics). – Forms of energy such as work (power) and heat, internal energy and enthalpy. – Entropy and the 2nd law of thermodynamics. – Reasons for thermodynamic losses in the form of irreversibilities. – The quality of different forms of energy measured as the ability to produce work. – Destruction of energy quality in processes. – Ideal gas model, its assumptions, applications and limitations. – Different cyclic processes such as Carnot, Rankine, Otto, Diesel and Brayton. The course gives the student insight about: – Operation of steam and gas based power stations, internal combustion engines, heat pumps and refrigeration cycles. – The main components of heat & power processes, such as steam and gas turbines, compressors, pumps, fans, heat exchangers and valves. – The ability of fluids to change phase (solid, liquid and gas).
TEP4120 Thermodynamics HELP(EXAM HELP, ONLINE TUTOR)
For a paramagnetic ideal gas, obeying both the Curie’s law and the ideal gas equation of state, show that the entropy is given by,
$$
S=C_{V, M} \ln T+n R \ln V-\frac{\mu_0 M^2}{2 C_C}+\text { const., }
$$
where $C_{V, M}$ is the heat capacity at constant volume and magnetization, assumed constant, and $C_C$ is the Curie constant.
5 points
A hydrostatic system of constant heat capacity, $C_P$ and at a temperature $T_i$ is put in contact with a reservoir at a higher temperature $T_f$. The pressure remains constant while the body comes to equilibrium with the reservoir. Show that the entropy change of the universe is equal to
$$
C_P[x-\ln (1+x)]
$$
where $x=-\left(T_f-T_i\right) / T_f$. Prove that this entropy change is positive.
$$
5+2=7 \text { points }
$$
Show that for a hydrostatic system,
$$
\left(\frac{\partial H}{\partial T}\right)_P=C_P
$$
and,
$$
\left(\frac{\partial H}{\partial P}\right)_T=-\mu C_P
$$
where $\mu \equiv\left(\frac{\partial T}{\partial P}\right)_H$ is the Joule-Thomson coefficient and $H$ is the enthalpy of the system. For an ideal gas, $\mu=0$. Show that for an ideal gas, $H=H(T)$, i.e. the enthalpy is purely a function of the temperature.
$2+2+2=6$ points
List a consistent set of assumptions required to employ each of the following equations. Possible assumptions include: closed system, open system, steady state, adiabatic, no work, negligible changes in potential energy, negligible changes in kinetic energy, isothermal, constant pressure, incompressible, ideal gas, constant specific heats. Show how the simplified equation is developed from a basic equation.
$$
\begin{aligned}
& \Delta u=c \Delta T \
& \Delta h=c \Delta T \
& \Delta h=c_p \Delta T \
& \Delta h=\Delta u+v \Delta p
\end{aligned}
$$

MY-ASSIGNMENTEXPERT™可以为您提供CATALOG.WINONA.EDU PHYS451 QUANTUM MECHANICS量子力学课程的代写代考和辅导服务