如果你也在 怎样代写现代代数Modern Algebra 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。现代代数Modern Algebra有时被称为代数结构或抽象代数，或者仅仅在高等数学的背景下被称为代数。虽然这个名字可能只是暗示了一种新的方式来表示微积分之前的代数，但实际上它比微积分更广泛、更深入。

现代代数Modern Algebra这门学科的思想和方法几乎渗透到现代数学的每一个部分。此外，没有一门学科更适合培养处理抽象概念的能力，即理解和处理问题或学科的基本要素。这包括阅读数学的能力，提出正确的问题，解决问题，运用演绎推理，以及写出正确、切中要害、清晰的数学。

现代代数Modern Algebra代写，免费提交作业要求， 满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕 博写手团队，所有订单可靠准时，保证 100% 原创。最高质量的现代代数Modern Algebra作业代写，服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。 由于作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此现代代数Modern Algebra作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

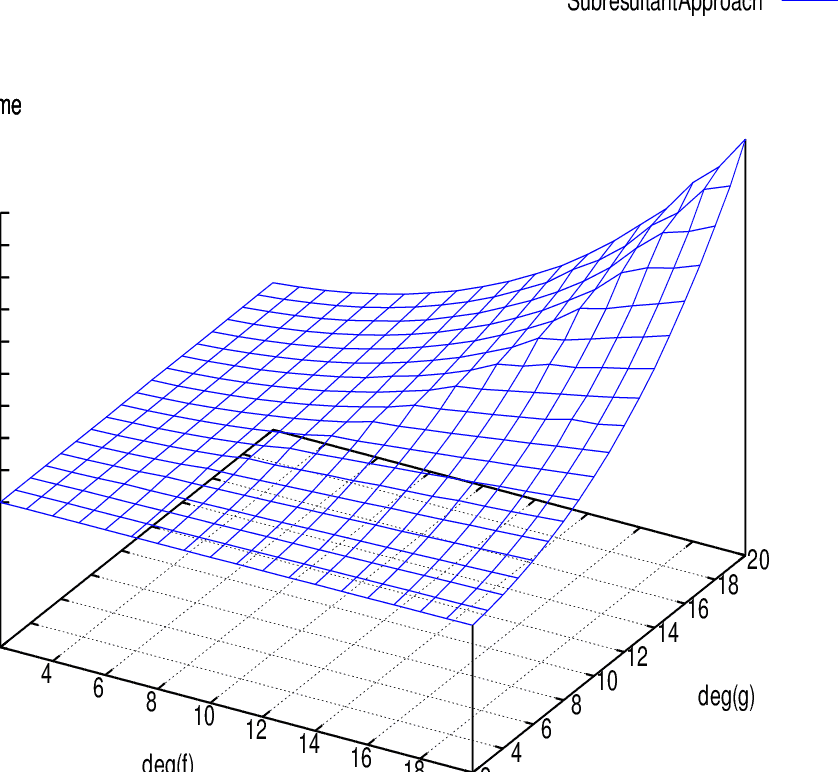
数学代写|现代代数代考Modern Algebra代写|Subresultants

In this section, we extend the resultant theory-which governs the gcd-to the subresultants which cover all results of the Extended Euclidean Algorithm. As before, this leads to efficient modular methods, but now for the whole algorithm. The reader only interested in efficient gcd algorithms may skip this and proceed directly to the implementation report in Section 6.13.

So now let $F$ be an arbitrary field, and $f, g \in F[x]$ nonzero of degrees $n \geq m$, respectively. We use the notation for the results of the Extended Euclidean Algorithm, as in (1) on page 141 , and $n_i=\operatorname{deg} r_i$ for $0 \leq i \leq \ell+1$, with $r_{\ell+1}=0$ and $\operatorname{deg} r_{\ell+1}=-\infty$.
THEOREM 6.47 .
Let $0 \leq k \leq m \leq n$. Then $k$ does not appear in the degree sequence if and only if there exist $s, t \in F[x]$ satisfying
$$
t \neq 0, \quad \operatorname{deg} s<m-k, \quad \operatorname{deg} t<n-k, \quad \operatorname{deg}(s f+t g)<k .
$$
Proof. ” $\Longrightarrow “$ : Suppose that $k$ does not appear in the degree sequence. Then there exists an $i$ with $2 \leq i \leq \ell+1$ such that $n_i<k<n_{i-1}$. We claim that $s=s_i$ and $t=t_i$ do the job. We have $s f+t g=r_i$, and $\operatorname{deg} r_i=n_i<k$. Furthermore, from Lemma 3.15 (b) we have
$$
\begin{aligned}
\operatorname{deg} s & =m-n_{i-1}<m-k, \
0 \leq \operatorname{deg} t & =n-n_{i-1}<n-k .
\end{aligned}
$$
The case $i=\ell+1$ gives $s=g / r_{\ell}$ and $t=-f / r_{\ell}$, where $k<n_{\ell}$ and $r_{\ell+1}=0$.
” $=”:$ Suppose there exist $s, t \in F[x]$ satisfying (11). The Uniqueness Lemma 5.15 implies that there exist $i \in{1, \ldots, \ell+1}$ and $\alpha \in F[x] \backslash{0}$ such that $t=\alpha t_i$ and $r=s f+t g=\alpha r_i$. Then from Lemma 3.15 (b) we find
$$
\begin{aligned}
n-n_{i-1} & \leq \operatorname{deg} \alpha+n-n_{i-1}=\operatorname{deg}\left(\alpha t_i\right)=\operatorname{deg} t<n-k, \
n_i & \leq \operatorname{deg} \alpha+n_i=\operatorname{deg}\left(\alpha r_i\right)=\operatorname{deg} r<k .
\end{aligned}
$$
Together these imply that $n_i<k<n_{i-1}$, so that $k$ is between two consecutive remainder degrees and does not occur in the degree sequence.

数学代写|现代代数代考Modern Algebra代写|Modular Extended Euclidean Algorithms

In this section, we use the subresultants from Section 6.10 to prove a bound on the coefficients of the Extended Euclidean Algorithm 3.14 over $\mathbb{Q}[x]$ and $F(y)[x]$, and to derive modular algorithms for the results of the EEA.
THEOREM 6.52.
Let $f, g \in \mathbb{Z}[x]$ have degrees $n \geq m$ and max-norm $|f|_{\infty},|g|_{\infty}$ at most $A$, and let $\delta=\max \left{n_{i-1}-n_i: 1 \leq i \leq \ell\right}$ be the maximal degree difference of consecutive remainders. The results $r_i, s_i, t_i$ of the Extended Euclidean Algorithm 3.14 for $f$ and $g$ in $\mathbb{Q}[x]$ have numerators and denominators (in lowest terms) absolutely bounded by $B=(n+1)^n A^{n+m}$. The corresponding bound for $q_i$ and $\rho_i$ is $C=(2 B)^{\delta+2}$. The algorithm can be performed with $O\left(n^3 m \delta^2 \log ^2(n A)\right)$ word operations.

PROoF. Let $2 \leq i \leq \ell$ and $n_i=\operatorname{deg} r_i$. In the EEA, $s_i$ and $t_i$ form the unique solution to the system (12) of linear equations, so that $\sigma_{n_i} s_i, \sigma_{n_i} t_i$, and $\sigma_{n_i} r_i=\sigma_{n_i} s_i f+\sigma_{n_i} t_i g$ are in $\mathbb{Z}[x]$, and by Cramer’s rule 25.6 and Hadamard’s inequality 16.6 we have
$$
\begin{aligned}
\left|\sigma_{n_i}\right| & \leq|f|_2^{m-n_i}|g|_2^{n-n_i} \leq(n+1)^{n-n_i} A^{n+m-2 n_i} \leq B, \
\left|\sigma_{n_i} s_i\right|_{\infty} & \leq|f|_2^{m-n_i-1}|g|_2^{n-n_i} \leq(n+1)^{n-n_i-1 / 2} A^{n+m-2 n_i-1} \leq B, \
\left|\sigma_{n_i} t_i\right|_{\infty} & \leq|f|_2^{m-n_i}|g|_2^{n-n_i-1} \leq(n+1)^{n-n_i-1 / 2} A^{n+m-2 n_i-1} \leq B, \
\left|\sigma_{n_i} r_i\right|_{\infty} & =\left|\left(\sigma_{n_i} s_i\right) f+\left(\sigma_{n_i} t_i\right) g\right|_{\infty} \leq\left(n_i+1\right)\left(\left|\sigma_{n_i} s_i\right|_{\infty} \cdot|f|_{\infty}+\left|\sigma_{n_i} t_i\right|_{\infty} \cdot|g|_{\infty}\right) \
& \leq\left(n_i+1\right) \cdot 2(n+1)^{n-n_i-1 / 2} A^{n+m-2 n_i} \leq 2(n+1)^{1 / 2} B .
\end{aligned}
$$

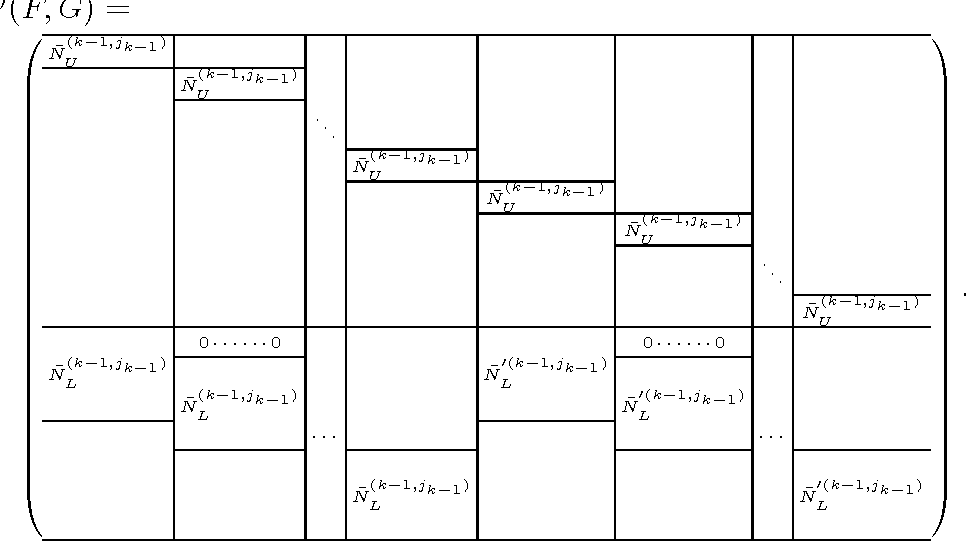
现代代数代写

数学代写|现代代数代考Modern Algebra代写|Subresultants

在本节中，我们将控制gcd的结果理论扩展到涵盖扩展欧几里得算法的所有结果的子结果。和以前一样，这导致了高效的模块化方法，但现在是整个算法。对高效gcd算法感兴趣的读者可以跳过这里，直接进入6.13节的实现报告。

现在设$F$为任意域，和$f, g \in F[x]$为非零度$n \geq m$。我们对扩展欧几里得算法的结果使用表示法，如第141页(1)所示，对$0 \leq i \leq \ell+1$使用$n_i=\operatorname{deg} r_i$，其中包含$r_{\ell+1}=0$和$\operatorname{deg} r_{\ell+1}=-\infty$。
定理6.47。
让$0 \leq k \leq m \leq n$。则当且仅当存在$s, t \in F[x]$满足时，$k$不出现在度序列中
$$
t \neq 0, \quad \operatorname{deg} s<m-k, \quad \operatorname{deg} t<n-k, \quad \operatorname{deg}(s f+t g)<k .
$$
证明。$\Longrightarrow “$:假设$k$不出现在度序列中。然后存在一个$i$和$2 \leq i \leq \ell+1$，使得$n_i<k<n_{i-1}$。我们声称$s=s_i$和$t=t_i$可以完成这项工作。我们有$s f+t g=r_i$和$\operatorname{deg} r_i=n_i<k$。更进一步，由引理3.15 (b)我们得到
$$
\begin{aligned}
\operatorname{deg} s & =m-n_{i-1}<m-k, \
0 \leq \operatorname{deg} t & =n-n_{i-1}<n-k .
\end{aligned}
$$
案例$i=\ell+1$给出$s=g / r_{\ell}$和$t=-f / r_{\ell}$，其中$k<n_{\ell}$和$r_{\ell+1}=0$。
“$=”:$假设存在$s, t \in F[x]$满足(11)。唯一性引理5.15暗示存在$i \in{1, \ldots, \ell+1}$和$\alpha \in F[x] \backslash{0}$，使得$t=\alpha t_i$和$r=s f+t g=\alpha r_i$。然后从引理3.15 (b)我们发现
$$
\begin{aligned}
n-n_{i-1} & \leq \operatorname{deg} \alpha+n-n_{i-1}=\operatorname{deg}\left(\alpha t_i\right)=\operatorname{deg} t<n-k, \
n_i & \leq \operatorname{deg} \alpha+n_i=\operatorname{deg}\left(\alpha r_i\right)=\operatorname{deg} r<k .
\end{aligned}
$$
它们合在一起意味着$n_i<k<n_{i-1}$，因此$k$位于两个连续的余数度数之间，不出现在度数序列中。

数学代写|现代代数代考Modern Algebra代写|Modular Extended Euclidean Algorithms

在本节中，我们使用第6.10节的子结果来证明扩展欧几里得算法3.14在$\mathbb{Q}[x]$和$F(y)[x]$上的系数的一个界，并推导出EEA结果的模块化算法。
定理6.52。
设$f, g \in \mathbb{Z}[x]$有度数$n \geq m$，最大范数$|f|{\infty},|g|{\infty}$最多为$A$，设$\delta=\max \left{n_{i-1}-n_i: 1 \leq i \leq \ell\right}$为连续余数的最大度数差。对于$\mathbb{Q}[x]$中的$f$和$g$，扩展欧几里得算法3.14的结果$r_i, s_i, t_i$的分子和分母(最低项)绝对以$B=(n+1)^n A^{n+m}$为界。$q_i$和$\rho_i$对应的绑定为$C=(2 B)^{\delta+2}$。该算法可以通过$O\left(n^3 m \delta^2 \log ^2(n A)\right)$字操作来执行。

证明。让$2 \leq i \leq \ell$和$n_i=\operatorname{deg} r_i$。在EEA中，$s_i$和$t_i$构成线性方程组(12)的唯一解，因此$\sigma_{n_i} s_i, \sigma_{n_i} t_i$和$\sigma_{n_i} r_i=\sigma_{n_i} s_i f+\sigma_{n_i} t_i g$在$\mathbb{Z}[x]$中，根据Cramer规则25.6和Hadamard不等式16.6，我们有
$$
\begin{aligned}
\left|\sigma_{n_i}\right| & \leq|f|2^{m-n_i}|g|_2^{n-n_i} \leq(n+1)^{n-n_i} A^{n+m-2 n_i} \leq B, \ \left|\sigma{n_i} s_i\right|{\infty} & \leq|f|_2^{m-n_i-1}|g|_2^{n-n_i} \leq(n+1)^{n-n_i-1 / 2} A^{n+m-2 n_i-1} \leq B, \ \left|\sigma{n_i} t_i\right|{\infty} & \leq|f|_2^{m-n_i}|g|_2^{n-n_i-1} \leq(n+1)^{n-n_i-1 / 2} A^{n+m-2 n_i-1} \leq B, \ \left|\sigma{n_i} r_i\right|{\infty} & =\left|\left(\sigma{n_i} s_i\right) f+\left(\sigma_{n_i} t_i\right) g\right|{\infty} \leq\left(n_i+1\right)\left(\left|\sigma{n_i} s_i\right|{\infty} \cdot|f|{\infty}+\left|\sigma_{n_i} t_i\right|{\infty} \cdot|g|{\infty}\right) \
& \leq\left(n_i+1\right) \cdot 2(n+1)^{n-n_i-1 / 2} A^{n+m-2 n_i} \leq 2(n+1)^{1 / 2} B .
\end{aligned}
$$

数学代写|现代代数代考Modern Algebra代写 请认准exambang™. exambang™为您的留学生涯保驾护航。