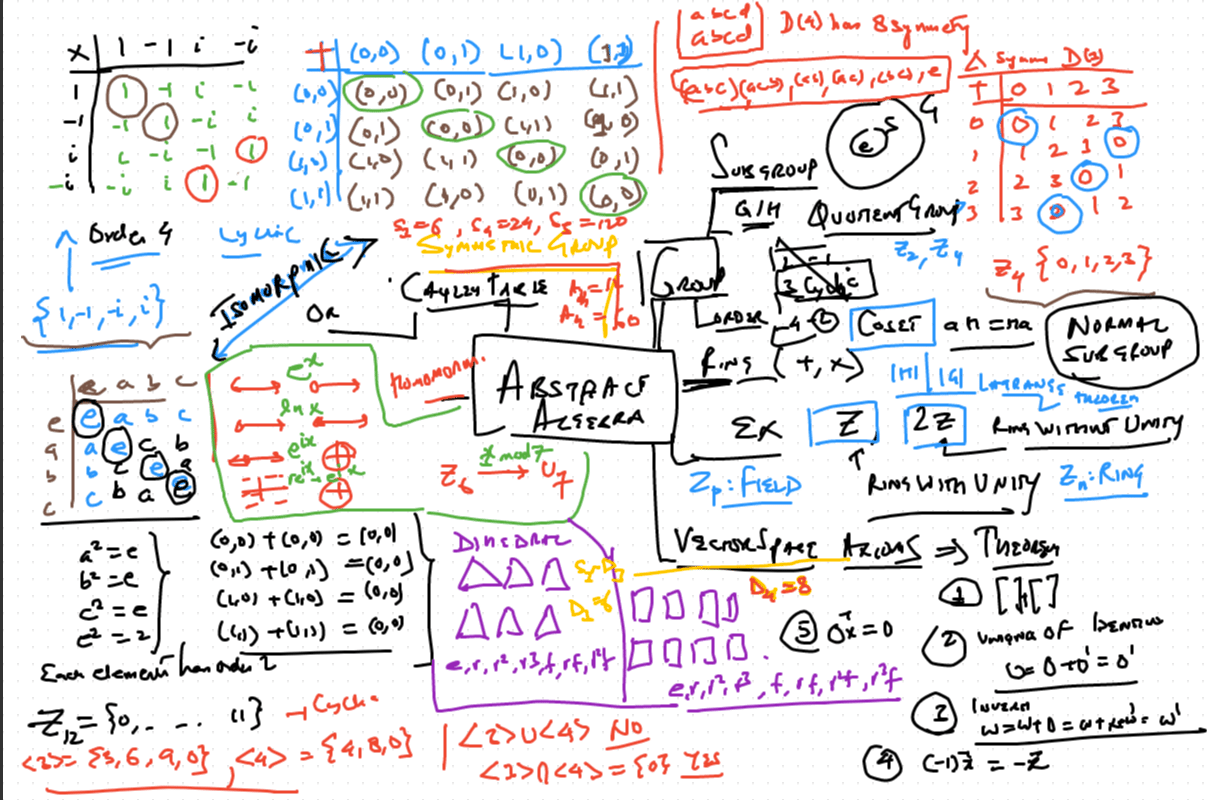
如果你也在 怎样代写现代代数Modern Algebra 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。现代代数Modern Algebra有时被称为代数结构或抽象代数，或者仅仅在高等数学的背景下被称为代数。虽然这个名字可能只是暗示了一种新的方式来表示微积分之前的代数，但实际上它比微积分更广泛、更深入。

现代代数Modern Algebra这门学科的思想和方法几乎渗透到现代数学的每一个部分。此外，没有一门学科更适合培养处理抽象概念的能力，即理解和处理问题或学科的基本要素。这包括阅读数学的能力，提出正确的问题，解决问题，运用演绎推理，以及写出正确、切中要害、清晰的数学。

现代代数Modern Algebra代写，免费提交作业要求， 满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕 博写手团队，所有订单可靠准时，保证 100% 原创。最高质量的现代代数Modern Algebra作业代写，服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。 由于作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此现代代数Modern Algebra作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

数学代写|现代代数代考Modern Algebra代写|Permutations and Inverses

A one-to-one correspondence from a set $A$ to itself is called a permutation on $A$. For any nonempty set $A$, we adopt the notation $\mathcal{S}(A)$ as standard for the set of all permutations on $A$. The set of all mappings from $A$ to $A$ will be denoted by $\mathcal{M}(A)$.

From the discussion at the end of Section 1.2, we know that composition of mappings is an associative binary operation on $\mathcal{M}(A)$. The identity mapping $I_A$ is defined by
$$
I_A(x)=x \text { for all } x \in A .
$$
For any $f$ in $\mathcal{M}(A)$,
$$
\left(I_A \circ f\right)(x)=I_A(f(x))=f(x)
$$
and
$$
\left(f \circ I_A\right)(x)=f\left(I_A(x)\right)=f(x)
$$
so $I_A \circ f=f \circ I_A=f$. That is, $I_A$ is an identity element for mapping composition. Once an identity element is established for a binary operation, the next natural question is whether inverses exist. Consider the mappings in the next example.

Example 1 In Example 1 of Section 1.3, we defined the mappings $f: \mathbf{Z} \rightarrow \mathbf{Z}$ and $g: \mathbf{Z} \rightarrow \mathbf{Z}$ by
$$
f(n)=2 n
$$
and
$$
g(n)= \begin{cases}\frac{n}{2} & \text { if } n \text { is even } \ 4 & \text { if } n \text { is odd. }\end{cases}
$$
For these mappings, $(g \circ f)(n)=n$ for all $n \in \mathbf{Z}$, so $g \circ f=I_Z$ and $g$ is a left inverse for $f$. Note, however, that
$$
(f \circ g)(n)= \begin{cases}n & \text { if } n \text { is even } \ 8 & \text { if } n \text { is odd }\end{cases}
$$

数学代写|现代代数代考Modern Algebra代写|Matrices

The word matrix is used in mathematics to denote a rectangular array of elements in rows and columns. The elements in the array are usually numbers, and brackets may be used to mark the beginning and the end of the array. Two illustrations of this type of matrix are
$$
\left[\begin{array}{rrrr}
5 & -1 & 0 & 3 \
2 & 1 & -2 & 7 \
4 & -6 & 4 & 3
\end{array}\right] \text { and }\left[\begin{array}{rr}
9 & 1 \
-1 & 0 \
6 & -3
\end{array}\right]
$$
The formal notation for a matrix is introduced in the following definition. We shall soon see that this notation is extremely useful in proving certain facts about matrices.
An $\boldsymbol{m}$ by $\boldsymbol{n}$ matrix over a set $S$ is a rectangular array of elements of $S$, arranged in $m$ rows and $n$ columns. It is customary to write an $m$ by $n$ matrix using notation such as
$$
A=\left[\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1 n} \
a_{21} & a_{22} & \cdots & a_{2 n} \
\vdots & \vdots & & \vdots \
a_{m 1} & a_{m 2} & \cdots & a_{m n}
\end{array}\right],
$$
where the uppercase letter $A$ denotes the matrix and the lowercase $a_{i j}$ denotes the element in row $i$ and column $j$ of the matrix $A$. The rows are numbered from the top down, and the columns are numbered from left to right. The matrix $A$ is referred to as a matrix of dimen$\operatorname{sion} m \times n$ (read ” $m$ by $n$ “).

现代代数代写

数学代写|现代代数代考Modern Algebra代写|Permutations and Inverses

集合$A$与自身的一对一对应称为$A$上的置换。对于任意非空集合$A$，我们采用$\mathcal{S}(A)$作为$A$上所有排列集合的标准符号。从$A$到$A$的所有映射集将用$\mathcal{M}(A)$表示。

从1.2节末尾的讨论中，我们知道映射的组合是$\mathcal{M}(A)$上的关联二进制操作。身份映射$I_A$由
$$
I_A(x)=x \text { for all } x \in A .
$$
对于$\mathcal{M}(A)$中的任何$f$，
$$
\left(I_A \circ f\right)(x)=I_A(f(x))=f(x)
$$
和
$$
\left(f \circ I_A\right)(x)=f\left(I_A(x)\right)=f(x)
$$
所以$I_A \circ f=f \circ I_A=f$。也就是说，$I_A$是用于映射组合的标识元素。一旦建立了二元运算的单位元素，下一个自然的问题是逆是否存在。考虑下一个示例中的映射。

在第1.3节的例1中，我们定义了映射$f: \mathbf{Z} \rightarrow \mathbf{Z}$和$g: \mathbf{Z} \rightarrow \mathbf{Z}$
$$
f(n)=2 n
$$
和
$$
g(n)= \begin{cases}\frac{n}{2} & \text { if } n \text { is even } \ 4 & \text { if } n \text { is odd. }\end{cases}
$$
对于这些映射，$(g \circ f)(n)=n$表示所有$n \in \mathbf{Z}$，因此$g \circ f=I_Z$和$g$是$f$的左逆。但是，请注意
$$
(f \circ g)(n)= \begin{cases}n & \text { if } n \text { is even } \ 8 & \text { if } n \text { is odd }\end{cases}
$$

数学代写|现代代数代考Modern Algebra代写|Matrices

“矩阵”一词在数学中用来表示按行和列排列的元素的矩形数组。数组中的元素通常是数字，括号可以用来标记数组的开始和结束。这类矩阵的两个例子是
$$
\left[\begin{array}{rrrr}
5 & -1 & 0 & 3 \
2 & 1 & -2 & 7 \
4 & -6 & 4 & 3
\end{array}\right] \text { and }\left[\begin{array}{rr}
9 & 1 \
-1 & 0 \
6 & -3
\end{array}\right]
$$
矩阵的正式符号将在下面的定义中介绍。我们很快就会看到，这个符号在证明关于矩阵的某些事实时是非常有用的。
集合$S$上的$\boldsymbol{m}$ × $\boldsymbol{n}$矩阵是一个包含$S$元素的矩形数组，按$m$行和$n$列排列。习惯上写一个$m$ × $n$的矩阵，使用这样的符号
$$
A=\left[\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1 n} \
a_{21} & a_{22} & \cdots & a_{2 n} \
\vdots & \vdots & & \vdots \
a_{m 1} & a_{m 2} & \cdots & a_{m n}
\end{array}\right],
$$
其中大写字母$A$表示矩阵，小写字母$a_{i j}$表示矩阵$A$的行$i$和列$j$中的元素。行从上到下编号，列从左到右编号。矩阵$A$被称为维度$\operatorname{sion} m \times n$的矩阵(读作“$m$ by $n$”)。

数学代写|现代代数代考Modern Algebra代写 请认准exambang™. exambang™为您的留学生涯保驾护航。