MY-ASSIGNMENTEXPERT™可以为您提供my.uq.edu.au MATH2401 Mathematical Analysis数学分析的代写代考和辅导服务!
这是昆士兰大学 数学分析课程的代写成功案例。
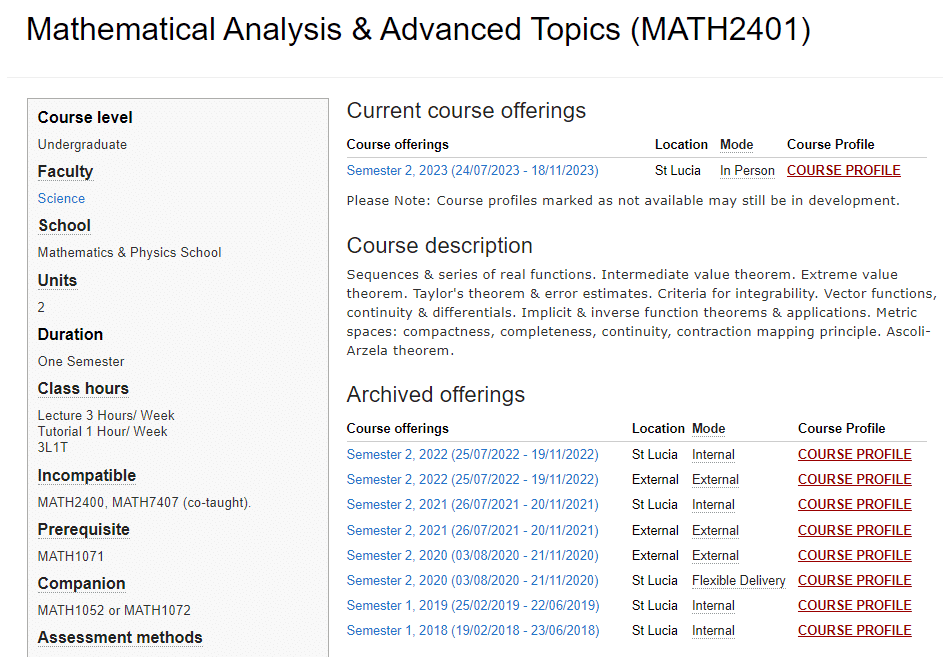
MATH2401课程简介
Sequences & series of real functions. Intermediate value theorem. Extreme value theorem. Taylor’s theorem & error estimates. Criteria for integrability. Vector functions, continuity & differentials. Implicit & inverse function theorems & applications. Metric spaces: compactness, completeness, continuity, contraction mapping principle. Ascoli-Arzela theorem.
Prerequisites
Contact Hours Per Week: LEC 3 Hours/ Week TUT 1 Hour/ Week 3L1T
Pre-Requisites: MATH1071
Companions: MATH1052 or MATH1072
Incompatible: MATH2400, MATH7407 (co-taught).
This is an advanced course designed to challenge students. Those interested in MATH2401 should have recieved a grade of 6 or 7 in MATH1071. If you do not meet these criteria, you are strongly advised to take MATH2400. Although not a prerequisite, familiarity with the course material of MATH1061 is helpful.
MATH2401 Mathematical Analysis HELP(EXAM HELP, ONLINE TUTOR)
(8 in Rudin) Prove that no order can be defined in the complex field that turns it into an ordered field. Hint: -1 is a square.
(10 in Rudin) Suppose $z=a+i b, w=u+i v$, and
$$
a=\left(\frac{|w|+u}{2}\right)^{1 / 2}, \quad b=\left(\frac{|w|-u}{2}\right)^{1 / 2} .
$$
Prove that $z^2=w$ if $v \geq 0$ and that $(\bar{z})^2=w$ if $v \leq 0$. Conclude that every complex number (with one exception!) has two complex square roots.
(13 in Rudin, this is often called the Reverse Traingle Inequality) If $x, y$ are complex, prove that
$$
|| x|-| y|| \leq|x-y| \text {. }
$$
(15 in Rudin) Under what conditions does equality hold in the Cauchy-Schwarz inequality? Recall that the aformentioned inequality says that if $a_1, a_2, \ldots, a_n$ and $b_1, b_2, \ldots, b_n$ are complex numbers, then
$$
\left|\sum_{j=1}^n a_j \bar{b}j\right|^2 \leq \sum{j=1}^n\left|a_j\right|^2 \sum_{j=1}^n\left|b_j\right|^2 .
$$
Bonus Problem (#7 in Rudin) Fix $b>1, y>0$, and prove that there is a unique real $x$ such that $b^x=y$, by completing the following outline. (This is called the logarithm of $y$ to the base $b$.)
(a) For any positive integer $n, b^n-1 \geq n(b-1)$.
(b) Hence $b-1 \geq n\left(b^{1 / n}-1\right)$.
(c) If $t>1$ and $n>(b-1) /(t-1)$, then $b^{1 / n}y$, then $b^{w-(1 / n)}>y$ for sufficiently large $n$.
(f) Let $A$ be the set of all $w$ such that $b^w<y$, and show that $x=\sup A$ satisfies $b^x=y$.
(g) Prove that this $x$ is unique.
MY-ASSIGNMENTEXPERT™可以为您提供my.uq.edu.au MATH2401 Mathematical Analysis数学分析的代写代考和辅导服务!