MY-ASSIGNMENTEXPERT™可以为您提供sydney. CSYS5030 Information Theory信息论课程的代写代考和辅导服务!
这是悉尼大学信息论课程的代写成功案例。

CSYS5030课程简介
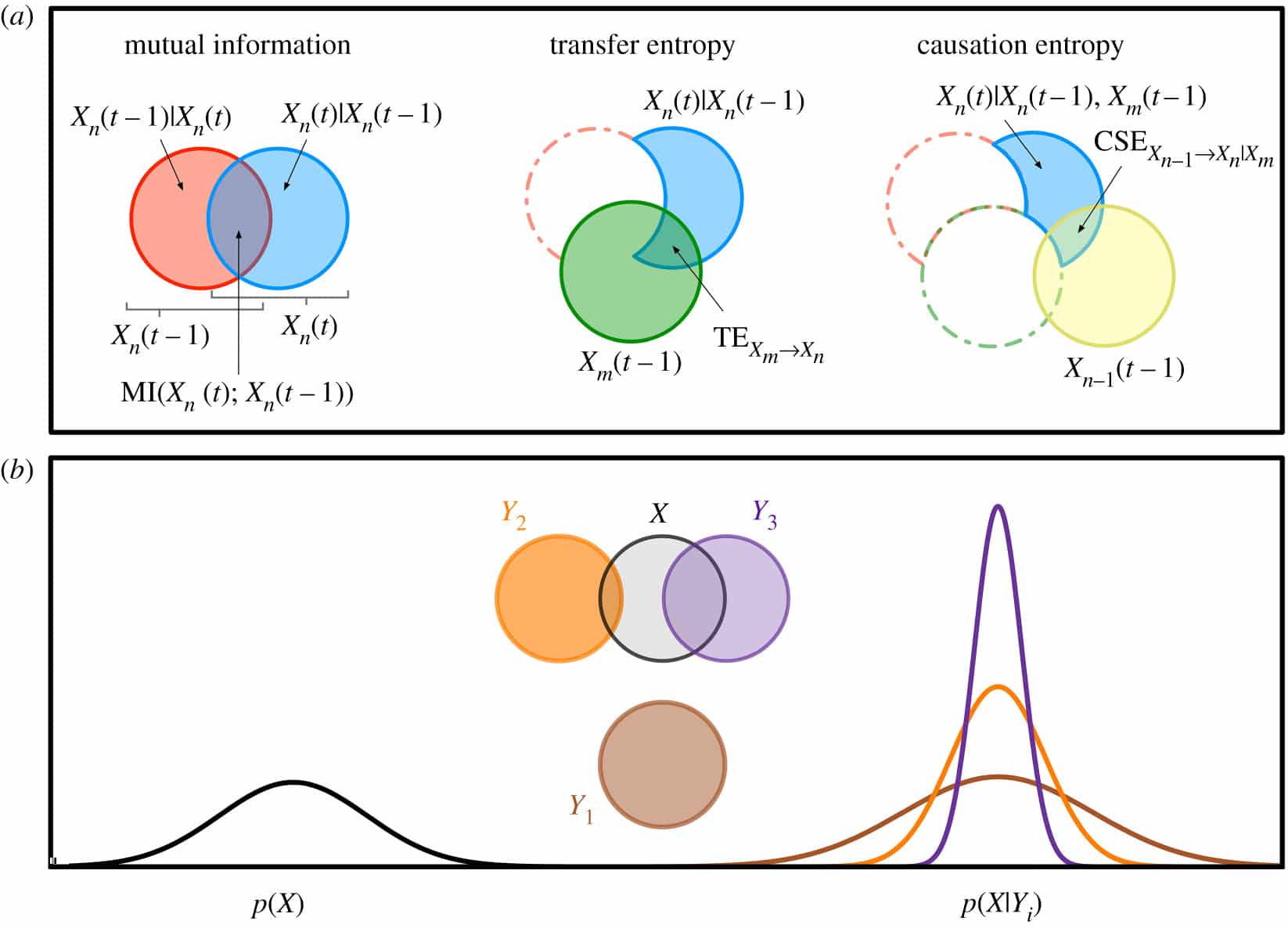
The dynamics of complex systems are often described in terms of how they process information and self-organise; for example regarding how genes store and utilise information, how information is transferred between neurons in undertaking cognitive tasks, and how swarms process information in order to collectively change direction in response to predators. The language of information also underpins many of the central concepts of complex adaptive systems, including order and randomness, self-organisation and emergence. Shannon information theory, which was originally founded to solve problems of data compression and communication, has found contemporary application in how to formalise such notions of information in the world around us and how these notions can be used to understand and guide the dynamics of complex systems. This unit of study introduces information theory in this context of analysis of complex systems, foregrounding empirical analysis using modern software toolkits, and applications in time-series analysis, nonlinear dynamical systems and data science. Students will be introduced to the fundamental measures of entropy and mutual information, as well as dynamical measures for time series analysis and information flow such as transfer entropy, building to higher-level applications such as feature selection in machine learning and network inference. They will gain experience in empirical analysis of complex systems using comprehensive software toolkits, and learn to construct their own analyses to dissect and design the dynamics of self-organisation in applications such as neural imaging analysis, natural and robotic swarm behaviour, characterisation of risk factors for and diagnosis of diseases, and financial market dynamics.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. critically evaluate investigations of self-organisation and relationships in complex systems using information theory, and the insights provided
- LO2. develop scientific programming skills which can be applied in complex system analysis and design
- LO3. apply and make informed decisions in selecting and using information-theoretic measures, and software tools to analyse complex systems
- LO4. create information-theoretic analyses of real-world data sets, in particular in a student’s domain area of expertise
- LO5. understand basic information-theoretic measures, and advanced measures for time-series, and how to use these to analyse and dissect the nature, structure, function, and evolution of complex systems
- LO6. understand the design of, and to extend the design of a piece of software using techniques from class, and your own readings.
CSYS5030 Information Theory HELP(EXAM HELP, ONLINE TUTOR)
(Information Divergence) Let $\mathbf{p}=\left(p_1, \ldots, p_n\right)$ and $\mathbf{q}=\left(q_1, \ldots, q_n\right)$ probability distributions and define the “information distance” between them by the expression
$$
D(\mathbf{p} \mid \mathbf{q})=\sum_{i=1}^n p_i \log \frac{p_i}{q_i} .
$$
(This quantity is sometimes called relative entropy or Kullback-Leibler distance.) Verify the following properties.
- $D(\mathbf{p} \mid \mathbf{q}) \geq 0$ with equality if and only if $\mathbf{p}=\mathbf{q}$.
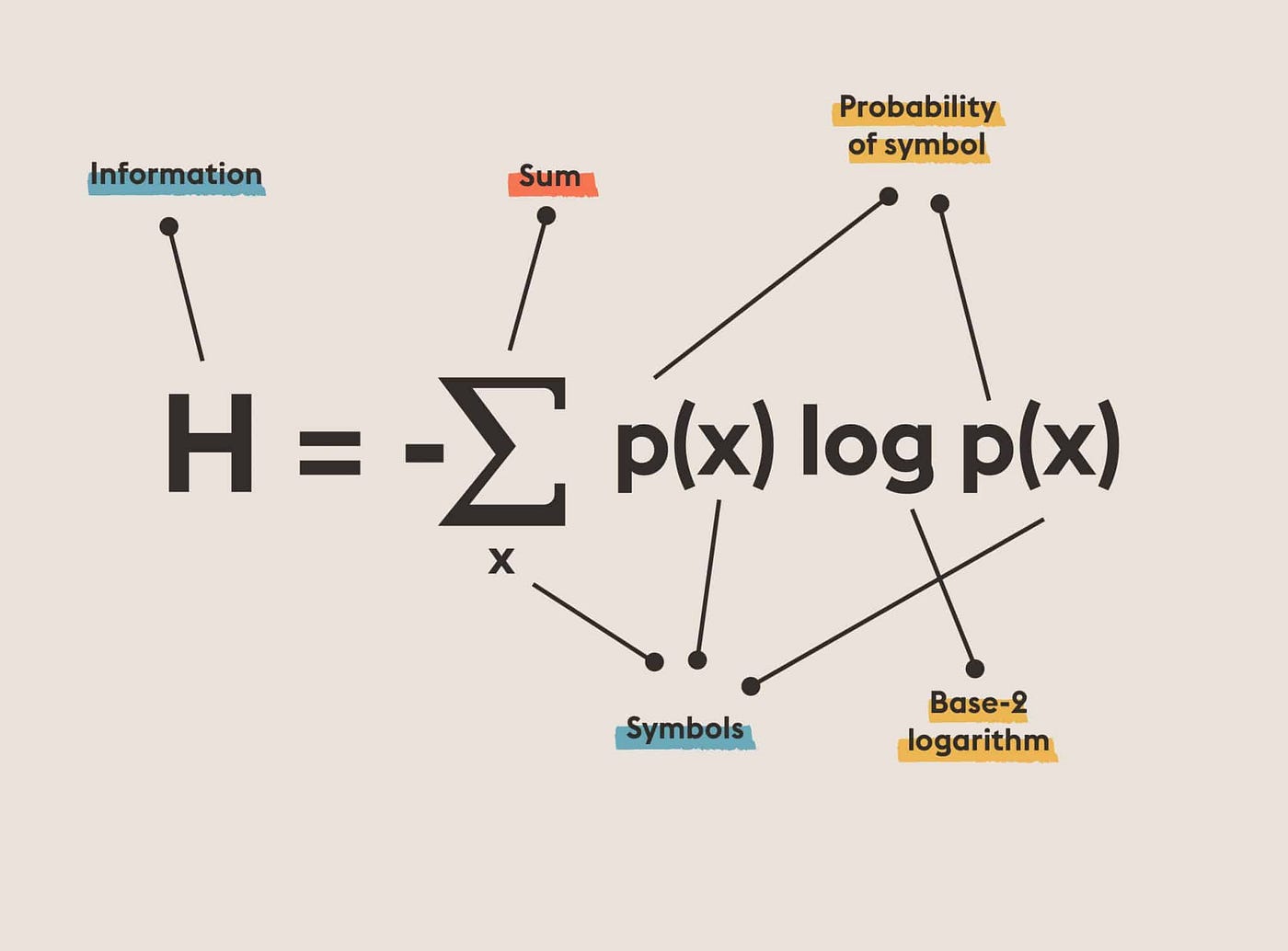
- $H(\mathbf{p})=\log n-D(\mathbf{p} \mid \mathbf{u})$, where $H(\mathbf{p})$ denotes the entropy of $\mathbf{p}$, and $\mathbf{u}$ denotes the uniform distribution on the set ${1, \ldots, n}$.
(Unknown Distribution) Assume that the random variable $X$ has distribution $\mathbf{p}=\left(p_1, \ldots, p_n\right)$, but this distribution is not known exactly. Instead, we are given the distribution $\mathbf{q}=\left(q_1, \ldots, q_n\right)$, and we design a Shannon-Fano code according to these probabilities, i.e., with codeword lengths $l_i=\left\lceil\log \frac{1}{q_i}\right\rceil$, $i=1, \ldots, n$. Show that the expected codeword length of the obtained code satisfies
$$
H(\mathbf{p})+D(\mathbf{p} \mid \mathbf{q}) \leq \sum_{i=1}^n p_i l_i<H(\mathbf{p})+D(\mathbf{p} \mid \mathbf{q})+1 .
$$
This means that the price we pay for not knowing the distribution exactly is about the information divergence (which is alway nonnegative).
(Horse RACING) $n$ horses run at a horse race, and the $i$-th horse wins with probability $p(i)$. If the $i$-th horse wins, the payoff is $o(i)>0$, i.e., if you bet $x$ Forints on horse $i$, you get xo $(i)$ Forints if horse $i$ wins, and zero Forints if any other horse wins. The race is run $k$ times without changing the probabilities and the odds. Let the random variables $X_1, \ldots, X_k$ denote the numbers of the winning horses in each round. Assume that you start with one unit of money, and in each round you invest all the money you have such that in each round the fraction of your money that you bet on horse $i$ is $b(i)\left(\sum_{i=1}^n b(i)=1\right)$. Clearly, after $k$ rounds your wealth is
$$
S_k=\prod_{i=1}^k b\left(X_i\right) o\left(X_i\right) .
$$
For a given distribution $\mathbf{p}=(p(1), \ldots, p(n))$ and betting strategy $\mathbf{b}=(b(1), \ldots, b(n))$, define
$$
W(\mathbf{b}, \mathbf{p})=\mathbf{E} \log \left(b\left(X_1\right) o\left(X_1\right)\right)=\sum_{i=1}^n p(i) \log (b(i) o(i)) .
$$
Show that
$$
S_k \approx 2^{k W(\mathbf{b}, \mathbf{p})}
$$
where $a_k \approx b_k$ means that $\lim _{k \rightarrow \infty} \frac{1}{k} \log \frac{a_k}{b_k}=0$, and the above convergence is meant in probability. Therefore, on a long run, maximizing $W(\mathbf{b}, \mathbf{p})$ results in the maximal wealth. Prove that the optimal betting strategy is $\mathbf{b}=\mathbf{p}$, i.e., you should distribute your money proportionally to the winning probabilities, independently of the odds (!!!).
(Shannon-Fano and Huffman codes) Let the random variable $X$ be distributed as
$$
(1 / 3 ; 1 / 3 ; 1 / 4 ; 1 / 12)
$$
Construct a Huffmann code. Show that there are two different optimal codes with codeword lengths $(1 ; 2 ; 3,3)$ and $(2 ; 2 ; 2 ; 2)$. Conclude that there exists an optimal code such that some of its codewords are longer than those of the corresponding Shannon-Fano code.

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY. CSYS5030 INFORMATION THEORY信息论课程的代写代考和辅导服务!