MY-ASSIGNMENTEXPERT™可以为您提供sydney. CSYS5030 Information Theory信息论课程的代写代考和辅导服务!
这是悉尼大学信息论课程的代写成功案例。
CSYS5030课程简介
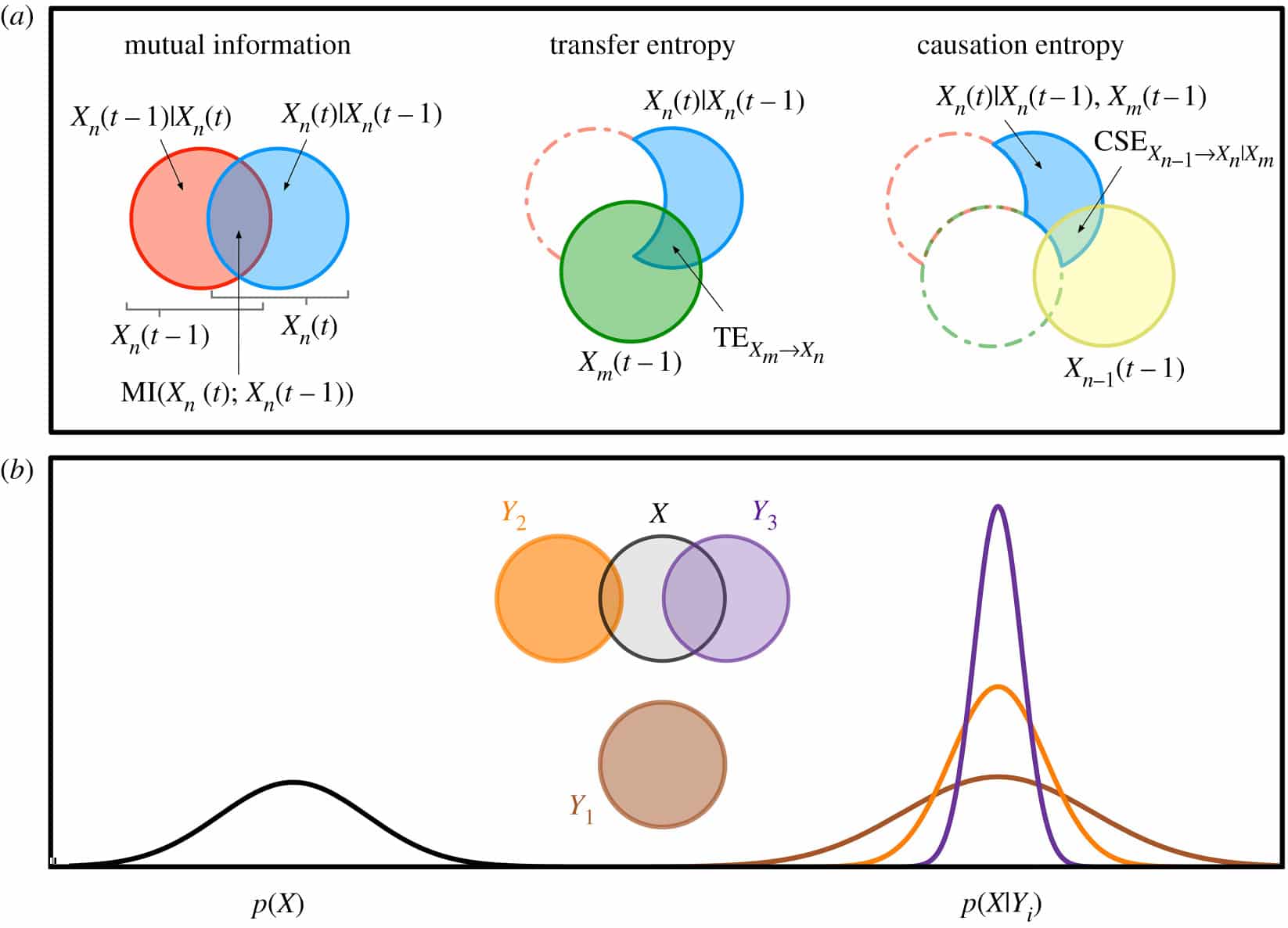
The dynamics of complex systems are often described in terms of how they process information and self-organise; for example regarding how genes store and utilise information, how information is transferred between neurons in undertaking cognitive tasks, and how swarms process information in order to collectively change direction in response to predators. The language of information also underpins many of the central concepts of complex adaptive systems, including order and randomness, self-organisation and emergence. Shannon information theory, which was originally founded to solve problems of data compression and communication, has found contemporary application in how to formalise such notions of information in the world around us and how these notions can be used to understand and guide the dynamics of complex systems. This unit of study introduces information theory in this context of analysis of complex systems, foregrounding empirical analysis using modern software toolkits, and applications in time-series analysis, nonlinear dynamical systems and data science. Students will be introduced to the fundamental measures of entropy and mutual information, as well as dynamical measures for time series analysis and information flow such as transfer entropy, building to higher-level applications such as feature selection in machine learning and network inference. They will gain experience in empirical analysis of complex systems using comprehensive software toolkits, and learn to construct their own analyses to dissect and design the dynamics of self-organisation in applications such as neural imaging analysis, natural and robotic swarm behaviour, characterisation of risk factors for and diagnosis of diseases, and financial market dynamics.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. critically evaluate investigations of self-organisation and relationships in complex systems using information theory, and the insights provided
- LO2. develop scientific programming skills which can be applied in complex system analysis and design
- LO3. apply and make informed decisions in selecting and using information-theoretic measures, and software tools to analyse complex systems
- LO4. create information-theoretic analyses of real-world data sets, in particular in a student’s domain area of expertise
- LO5. understand basic information-theoretic measures, and advanced measures for time-series, and how to use these to analyse and dissect the nature, structure, function, and evolution of complex systems
- LO6. understand the design of, and to extend the design of a piece of software using techniques from class, and your own readings.
CSYS5030 Information Theory HELP(EXAM HELP, ONLINE TUTOR)
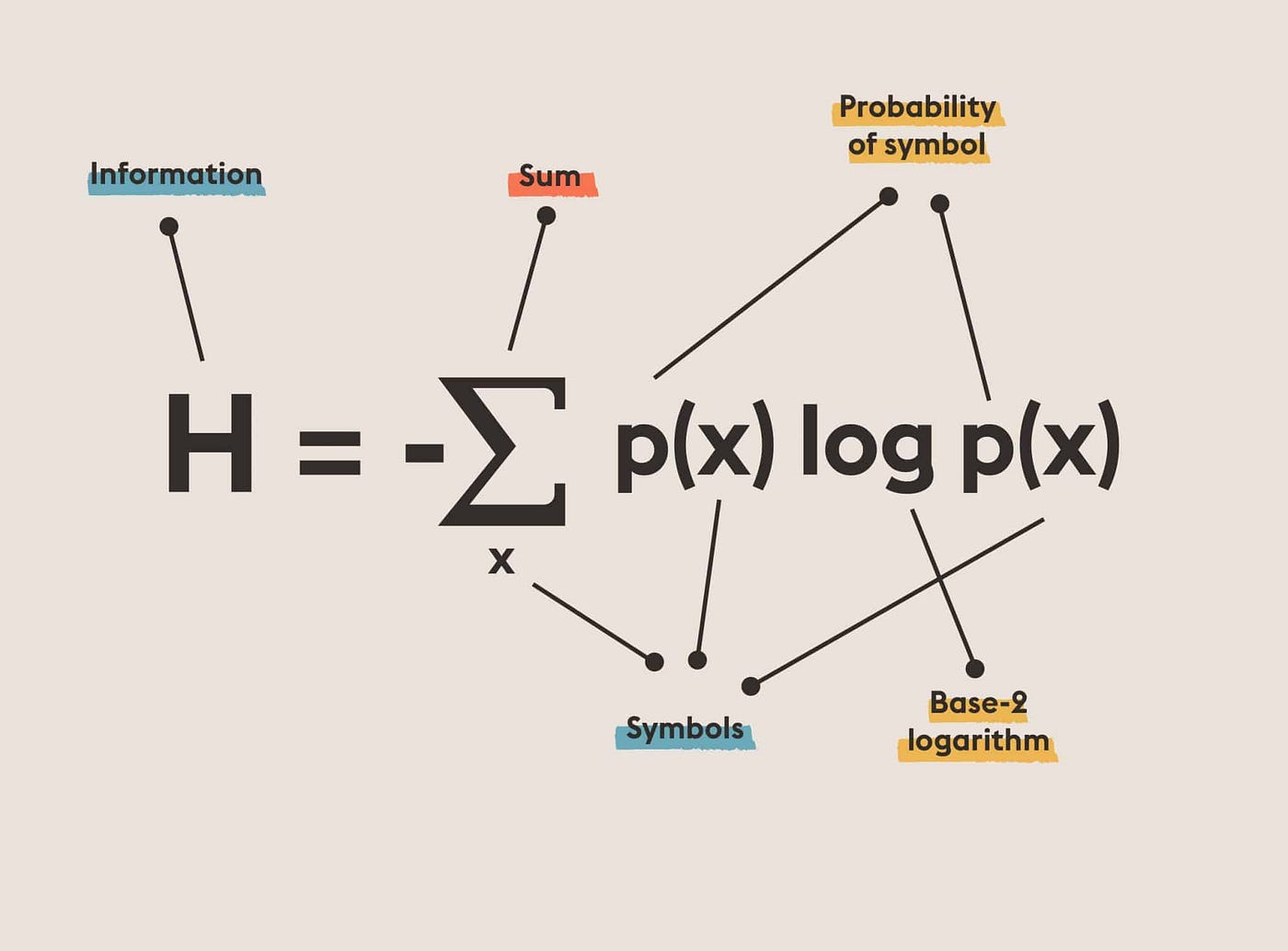
(Average Length of ThE optimal CODE) Show that the expected length of the codewords of the optimal binary code may be arbitrarily close to $H(X)+1$. More precisely, for any small $\epsilon>0$, construct a distribution on the source alphabet $\mathcal{X}$ such that the average codeword length of the optimal binary code satisfies
$$
\mathbf{E}|f(X)|>H(X)+1-\epsilon
$$
(EQUALITY IN KRAfT’s INEQUALITY) An $f$ prefix code is called full if it loses its prefix property by adding any new codeword to it. A string $\mathbf{x}$ is called undecodable if it is impossible to construct a sequence of codewords such that $\mathrm{x}$ is a prefix of their concatenation. Show that the following three statements are equivalent.
(a) $f$ is full,
(b) there is no undecodable string with respect to $f$,
(c) $\sum_{i=1}^n s^{-l_i}=1$, where $s$ is the cardinality of the code alphabet, $l_i$ is the codeword length of the $i$ th codeword, and $n$ is the number of codewords.
(Shannon-Fano Code) Consider the following code construction. Order the elements of the source alphabet $\mathcal{X}$ according to their decreasing probabilities: $p\left(x_1\right) \geq p\left(x_2\right) \geq \cdots \geq p\left(x_n\right)>0$. Introduce the numbers $w_i$ as follows:
$$
w_1=0, \quad w_i=\sum_{j=1}^{i-1} p\left(x_i\right) \quad(i=2, \ldots, n) .
$$
Consider the binary expansion of the numbers $w_i$. Write down the binary expansion of $w_i$ until the first bit such that the expansion differs from the expansion of all $w_j(j \neq i)$. Thus, we have obtained $n$ finite string. Define the binary codeword $f\left(x_i\right)$ as the obtained binary expansion of $w_i$ following the decimal point. Prove that the lengths of the codewords of the obtained code satisfy
$$
\left|f\left(x_i\right)\right|<-\log p\left(x_i\right)+1 .
$$
Therefore, the expected codeword length is smaller than the entropy plus one.
(BAD CODES) Which of the following binary codes cannot be a Huffman code for any distribution? Verify your answer.
(a) $0,10,111,101$
(b) $00,010,011,10,110$
(c) $1,000,001,010,011$
Assume that the probability of each element of the source alphabet $\mathcal{X}=\left{x_1, \ldots, x_n\right}$ is of the form $2^{-i}$, where $i$ is a positive integer. Prove that the Shannon-Fano code is optimal. Show that the average codeword length of a binary Huffman code is equal to the entropy if and only if the distribution is of the described form.

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY. CSYS5030 INFORMATION THEORY信息论课程的代写代考和辅导服务!