MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH1002 Linear Algebra线性代数的代写代考和辅导服务!
这是悉尼大学线性代数课程的代写成功案例。
MATH1002课程简介
MATH1002 is designed to provide a thorough preparation for further study in mathematics and statistics. It is a core unit of study providing three of the twelve credit points required by the Faculty of Science as well as a foundation requirement in the Faculty of Engineering. This unit of study introduces vectors and vector algebra, linear algebra including solutions of linear systems, matrices, determinants, eigenvalues and eigenvectors.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. apply mathematical logic and rigour to solving problems;
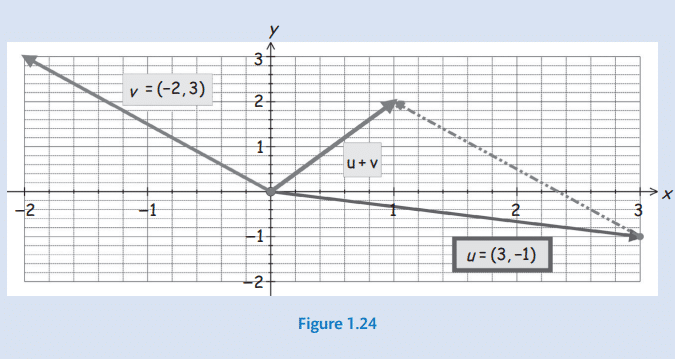
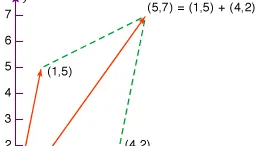
- LO2. represent vectors both algebraically and geometrically in two and three dimensions, and perform arithmetic with them;
- LO3. use vectors to solve classical geometric problems;
- LO4. determine spanning families and check linear independence
- LO5. perform and manipulate dot and cross products;
- LO6. set up systems of linear equations;
- LO7. solve systems of linear equations using Gaussian elimination;
- LO8. perform matrix arithmetic and calculate matrix inverses and determinants;
- LO9. find eigenvalues and eigenvectors;
- LO10. diagonalise a matrix;
- LO11. express mathematical ideas and arguments coherently in written form.
MATH1002 Linear algebra HELP(EXAM HELP, ONLINE TUTOR)
Consider the matrix
$$
A=\left[\begin{array}{lll}
2 & -3 & 1 \
1 & -2 & 1 \
1 & -3 & 2
\end{array}\right]
$$
1) Diagonalize $A$;
2) Use the diagonalization to find $A^{10}$;
3) Determine the invertibility of $A$ from its diagonalization.
4) Use the diagonalization to compute $A^5-2 A^4+A^3$.
The city of Clear Water Bay maintains a constant population of 30,000. A political science study estimated that there are 15,000 independents, 9,000 democrats, and 6,000 liberals. It was also estimated that each year $20 \%$ of democrats and $10 \%$ of liberals become independents $20 \%$ of independents and $10 \%$ of liberals become democrats, $10 \%$ of independents and $10 \%$ of democrats become liberals. Find the political composition of Clear Water Bay in the long run.
Determine whether the following statements are true or false (no reason needed).
1) If all eigenvalues of $A$ are 0 , then $A=0$;
2) If $A^9=0$, then all eigenvalues of $A$ vanish;
3) If $v$ is an eigenvector of $A$, then $v$ is an eigenvector of $A^2$;
4) If $v$ is an eigenvector of $A$, then $v$ is an eigenvector of $A^T$;
5) If $u$ and $v$ are eigenvectors of $A$, then $u+v$ is also an eigenvector of $A$;
6) If $u$ is an eigenvector of $A$, then $2 u$ is an eigenvector of $A$;
7) If $A$ and $B$ are diagonalizable, then $A B$ is diagonalizable:
8) If an invertible matrix $A$ is diagonalizable, then $A^{-1}$ is also diagonalizable:
9) Similar matrices have the same eigenvalues;
10) If two matrices have the same eigenvalues, then they are similar.
Consider
$$
A=\left[\begin{array}{ccc}
-1 & 6 & 6 \
3 & -8 & 3 \
1 & -2 & 6 \
1 & -4 & -3
\end{array}\right] \quad u=\left[\begin{array}{l}
1 \
0 \
0 \
0
\end{array}\right]
$$
1) Find an orthogonal basis of $\operatorname{Col} A$;
2) Find the orthogonal projection of $u$ on $\operatorname{Col} A$;
3) Find the distance from $u$ to $\operatorname{Col} A$.
Consider the polynomials
$$
\boldsymbol{p}_1=1+t-t^3, \boldsymbol{p}_2=2 t-t^2-t^3, \boldsymbol{p}_3=1-t+t^2, \boldsymbol{p}_4=2+t^2-t^3
$$
of $\mathbf{P}_3$, the vector space of polynomials of degree less or equal to 3 .
(a) Find a basis for the subspace $\operatorname{Span}\left{\boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3, \boldsymbol{p}_4\right}$;
(b) Find the coordinates of $\boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3, \boldsymbol{p}_4$ under the basis of in (a);
(c) Extend the basis in (a) to a basis for $\mathbf{P}_3$.

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY MATH1002 LINEAR ALGEBRA线性代数的代写代考和辅导服务!