MY-ASSIGNMENTEXPERT™可以为您提供my.uq.edu.au MATH2401 Mathematical Analysis数学分析的代写代考和辅导服务!
这是昆士兰大学 数学分析课程的代写成功案例。

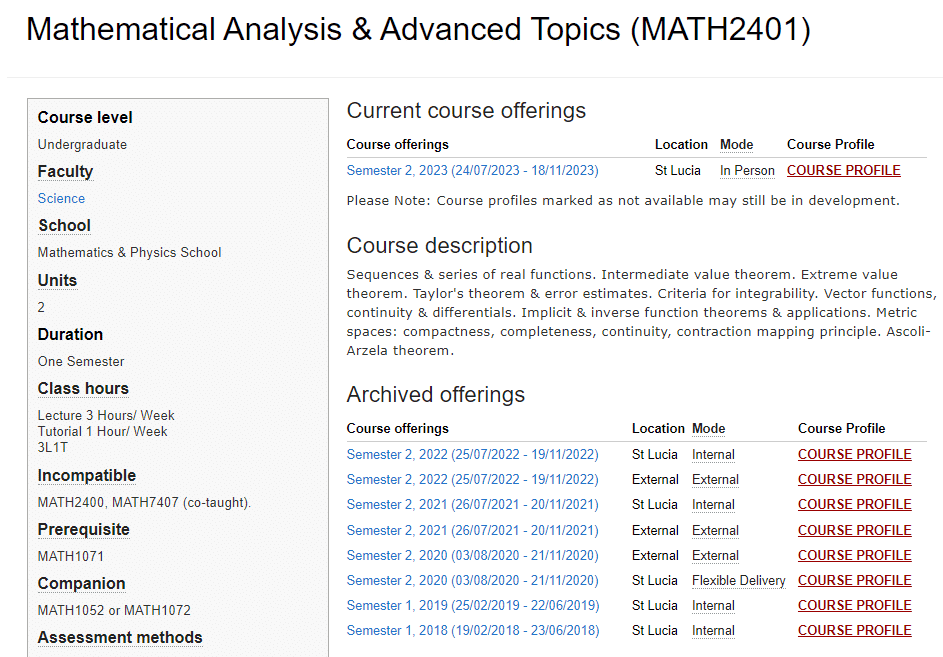
MATH2401课程简介
Sequences & series of real functions. Intermediate value theorem. Extreme value theorem. Taylor’s theorem & error estimates. Criteria for integrability. Vector functions, continuity & differentials. Implicit & inverse function theorems & applications. Metric spaces: compactness, completeness, continuity, contraction mapping principle. Ascoli-Arzela theorem.
Prerequisites
Contact Hours Per Week: LEC 3 Hours/ Week TUT 1 Hour/ Week 3L1T
Pre-Requisites: MATH1071
Companions: MATH1052 or MATH1072
Incompatible: MATH2400, MATH7407 (co-taught).
This is an advanced course designed to challenge students. Those interested in MATH2401 should have recieved a grade of 6 or 7 in MATH1071. If you do not meet these criteria, you are strongly advised to take MATH2400. Although not a prerequisite, familiarity with the course material of MATH1061 is helpful.
MATH2401 Mathematical Analysis HELP(EXAM HELP, ONLINE TUTOR)
Let $\left{f_n\right}$ be a uniformly bounded sequence of functions which are Riemann integrable on $[a, b]$, and put
$$
F_n(x)=\int_a^x f_n(t) d t(a \leq x \leq b)
$$
Prove that there exists a subsequence $\left{F_{n_k}\right}$ which converges uniformly on $[a, b]$.
If $f$ is continuous on $[0,1]$ and if
$$
\int_0^1 f(x) x^n d x=0(n=0,1,2, \ldots)
$$
Prove that $f(x)=0$ on $[0,1]$
Suppose that $p_n$ is a sequence of polynomials converging uniformly to $f$ on $[0,1]$ and $f$ is not a polynomial. Prove that the degrees of the $p_n$ are not bounded.[Hint: An Nth-degree polynomial $p$ is uniquely determined by its values at $N+1$ points $x_0, \ldots, x_N$ via Lagrange’s interpolation formula
$$
p(x)=\sum_{i=0}^N \pi_i(x) \frac{p\left(x_i\right)}{\pi_i\left(x_i\right)}
$$
where $\pi_i(x)=\left(x-x_0\right)\left(x-x_1\right) \ldots\left(x-x_N\right) /\left(x-x_i\right)$.
Let $\epsilon>0$ be given. Show that
$$
f(x)=\sum_{n=1}^{\infty} \frac{\cos n x}{e^{n x}}
$$
is uniform converge on $[\epsilon, \infty)$ but $f(x)$ is not uniform converge on $(0, \infty)$.
Show that $\mathrm{X}$ is Hausdorff if and only if the diagonal $\Delta={(x, x) \mid x \in X}$ is closed in $\mathrm{X} \times \mathrm{X}$.
MY-ASSIGNMENTEXPERT™可以为您提供my.uq.edu.au MATH2401 Mathematical Analysis数学分析的代写代考和辅导服务!