博弈论代写代考| What if Play Is Not Simultaneous? 数学代写
博弈论代考
Our first assumption to vary is the assumption that moves are made simultaneously and independently. What is affected by this change?
First consider constant-sum games. One place where we used the assumption of independent choice of strategies was when we derived the formula $E=p A q$ for expected payoffs. If the strategies are not chosen independently, then the probability of an outcome of the game (which is an intersection of two strategy choices) is not necessarily the product of the individual probabilities of the strategy choices, so the derivation of this formula $E=p A q$ breaks down. However, this will not turn out to be a be a problem, because on any one play of the game, we still assume both players are rational and skillful and have the same information about the payoffs. Thus, whoever moves second will know what strategy his or her opponent used in that play of the game and can using a mixed strategy in the long run. Furthermore, whoever is going first knows that the second player will respond this way, and so this will help him or her decide the best strategic choice even though he or she is moving first.
Here is another way to look at it. The concept of a mixed strategy was proposed to deal with the situation that if you used a pure strategy, that was tantamount to tipping your hand about what you were going to do in repeated play. Mixing the strategies on different plays was a way to keep your choice a secret so that your opponent could not take advantage of you. But if the choices are not made simultaneously, whoever goes second always knows what strategy the other player has used, so repeated play is no different than playing the game once. The second player can make his choice contingent on what the first player does, and the entire notion of a mixed strategy is more or less useless.
We have already observed in Chapter 6 that if a constant-sum game is strictly determined, secrecy is not necessary, and both players should just go for the saddle point no matter what. Thus, we suspect that non-simultaneous play will have no effect on how these games are played. However, in games without saddle points, we have already observed that secrecy is necessary (which is why mixed strategies were developed).
If you remove simultaneity, then you are removing any hope of secrecy for whoever moves first. Thus, constant-sum games that are not strictly determined should be played differently than with Let’s illustrate this with some examples.
Consider a zero-sum game with payoff matrix:
$$
A=\left[\begin{array}{ccc}
5 & -1 & 0 \
-1 & -3 & 2 \
-3 & -2 & -4
\end{array}\right]
$$
354 Sensitivity Analysis, Ordinal Games, and $n$-Person Games
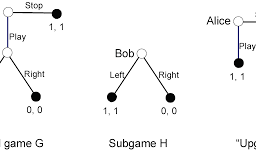
In this game, there is a saddle point $v=-1$ in the first row and second column. Suppose the row player goes second. If the column player chooses the first column, then the row player will choose the first row to get the 5 payoff (which is what the expected value principle recommends). If the column player chooses the second column, the row player again chooses the first row according to the expected value principle. If the column player chooses the third column, the row player chooses the second row. But now the column player knows all this and is skillful and rational. 2. Thus, he should choose the second column, precisely because it is the best of these worst-case scenarios. The rational outcome is indeed the saddle point.
The reader can no doubt make a similar analysis assuming the row player moves first, and again, the outcome is the saddle point. This illustrates that strictly determined constant-sum games are played the same whether the moves are simultaneous or not. The next example is not strictly determined:
$$
A=\left[\begin{array}{ccc}
0 & -1 & 1 \
1 & 0 & -1 \
-1 & 1 & 0
\end{array}\right]
$$
The reader should recognize that this is the payoff matrix for rock paper scissors. We already know the result of simultaneous play. It’s a fair game $(v=0)$ with optimal mixed strategies for both players to mix all three options with equal probability. But if the either player goes first and plays rock, the other player obviously should play paper to win. If the first player plays paper, the second responds with scissors to win, and if the first plays scissors, the second responds with rock to win. On any one play of the game, no matter what the first player does, he loses. Again, the second player responds according the expected value principle. This time, since the worst-case the strategies. Thus, the first player could always play the same thing, or she could vary the plays in any mix. It doesn’t matter, she always will lose a dollar.
The same argument works for any matrix without a saddle point. Whoever goes second will always use the expected value principle to select the best payoff, regardless of what his opponent does. Thus, whoever goes first knows he will always wind up at the worst payoff in his row or column. Thus, unless all these worst cases are a tie as in rock paper scissors, he should choose the strategy that has the best of the worst-case payoffs.
Our final example illustrates this:
我们的第一个变化假设是假设移动是同时且独立地进行的。这种变化有什么影响?
首先考虑恒和博弈。我们使用独立选择策略假设的一个地方是当我们推导出预期收益的公式 $E=p A q$ 时。如果策略不是独立选择的,那么博弈结果的概率(即两个策略选择的交集)不一定是策略选择的个体概率的乘积,所以这个公式的推导$E= p A q$ 崩溃。然而,这不会成为一个问题,因为在游戏的任何一次游戏中,我们仍然假设两个玩家都是理性和熟练的,并且具有相同的收益信息。因此,谁先走,谁就会知道他或她的对手在这场比赛中使用了什么策略,并且从长远来看可以使用混合策略。此外,无论谁先行,都知道第二个玩家会以这种方式做出反应,因此即使他或她先行,这也将有助于他或她做出最佳战略选择。
这是另一种看待它的方式。提出混合策略的概念是为了解决如果你使用纯粹的策略,那无异于在重复游戏中你将要做什么的问题。在不同的比赛中混合策略是一种让你的选择保密的方法,这样你的对手就无法利用你。但如果选择不是同时做出的,谁先出手就知道其他玩家使用了什么策略,所以重复游戏与玩一次游戏没有什么不同。第二个玩家可以根据第一个玩家的行为做出选择,而混合策略的整个概念或多或少是无用的。
我们在第 6 章中已经观察到,如果一个恒和博弈是严格确定的,那么保密是不必要的,无论如何双方都应该去寻找鞍点。因此,我们怀疑非同时游戏不会影响这些游戏的玩法。然而,在没有鞍点的游戏中,我们已经观察到保密是必要的(这就是开发混合策略的原因)。
如果你消除了同时性,那么你就消除了先行动者的任何保密希望。因此,不严格确定的常数和游戏应该与我们用一些例子来说明这一点不同。
考虑一个带有收益矩阵的零和游戏:
$$
A=\left[\begin{数组}{ccc}
5 & -1 & 0 \
-1 & -3 & 2 \
-3 & -2 & -4
\end{数组}\right]
$$
354 敏感性分析、序数博弈和 $n$-Person 博弈
在这个游戏中,第一行第二列有一个鞍点$v=-1$。假设排球员排在第二位。如果列玩家选择第一列,那么行玩家将选择第一行来获得 5 的收益(这是期望值原则所建议的)。如果列玩家选择第二列,行玩家再次根据期望值原则选择第一行。如果列玩家选择第三列,则行玩家选择第二行。但是现在的纵队玩家都知道这一切,而且熟练和理性。 2. 因此,他应该选择第二列,正是因为它是这些最坏情况中最好的。理性的结果确实是鞍点。
毫无疑问,读者可以进行类似的分析,假设排玩家首先移动,并且同样,结果是鞍点。这说明无论移动是否同时进行,严格确定的常数和博弈都是相同的。下一个例子没有严格确定:
$$
A=\left[\begin{数组}{ccc}
0 & -1 & 1 \
1 & 0 & -1 \
-1 & 1 & 0
\end{数组}\right]
$$
读者应该认识到这是石头剪刀布的收益矩阵。我们已经知道同时播放的结果。这是一个公平的游戏 $(v=0)$,具有最佳混合策略,让两个玩家以相等的概率混合所有三个选项。但如果任何一个玩家先玩摇滚,另一个玩家显然应该玩纸来赢。如果第一个玩家玩纸,那么第二个响应剪刀就赢了,如果第一个玩剪刀,第二个响应石头就赢了。在任何一次游戏中,无论第一个玩家做什么,他都输了。同样,第二个玩家根据期望值原则做出反应。这一次,自最坏情况的策略。因此,第一个玩家总是可以玩同样的东西,或者她可以在任何组合中改变游戏。没关系,她总是会损失一美元。
相同的论点适用于任何没有鞍点的矩阵。无论他的对手做什么,谁排在第二位总是会使用期望值原则来选择最好的回报。因此,无论谁先走,他都知道他总是会在他的行或列中得到最差的回报。因此,除非所有这些最坏的情况都是平局
博弈论代写
博弈论是关于什么的?当我妻子外出参加托斯卡纳的一个愉快的小型会议时,三位年轻女性邀请我与她们同桌共进午餐。当我坐下时,其中一个用闷热的声音说,“教我们如何玩爱情游戏”,但事实证明,他们想要的只是关于如何管理意大利男朋友的建议。我仍然认为他们拒绝我的战略建议是错误的,但他们正确地认为求爱是我们在现实生活中玩的许多不同类型的游戏之一在交通繁忙的司机正在玩驾驶游戏。在 eBay 上竞标的讨价还价者正在玩拍卖游戏。一家公司和一个工会正在谈判明年的工资,这是一场讨价还价的游戏。当反对的候选人在选举中选择他们的平台时,他们正在玩一场政治游戏。决定今天玉米片价格的杂货店老板正在玩一场经济游戏。简而言之,每当人类互动时,就会玩游戏。
每次新的巨额电信拍卖都需要根据将要运行的环境进行调整。不能像美国政府在聘请苏富比拍卖一堆卫星转发器时发现的那样,将设计从货架上拿下来。但也无法在数学模型中捕捉到新电信市场的所有复杂细节。因此,设计电信拍卖既是一门艺术,也是一门科学。一个人从简单的模型中推断出来,这些模型被选择来模仿似乎是问题的基本战略特征。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
博弈论,又称为对策论(Game Theory)、赛局理论等,既是现代数学的一个新分支,也是运筹学的一个重要学科。 博弈论主要研究公式化了的激励结构间的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法。 博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。