MY-ASSIGNMENTEXPERT™可以为您提供cornell.edu Physics6561 Electrodynamics电动力学课程的代写代考和辅导服务!
这是康乃尔大学电动力学课程的代写成功案例。
Physics6561课程简介
As an undergraduate you learn the language of physics, the laws of physics, and even some physics trivia. And thanks to the skill of your instructors, the subject hums like a well oiled machine. If there’s anything that’s daunting, occasionally, it’s some of the math that comes with the territory. But that’s incidental since you know that, fundamentally, physics is simple and elegant.
But by the time you’re a graduate student you realize that the world doesn’t always seem to play by the rules of the physics laid out in textbooks. There are subtleties, apparent contradictions, paradoxes. You find out that eventually these things got resolved, but when they first appeared on the radar they were called effects. Coming to terms with the effects of physics is a good way to think of the next phase of your education.
Prerequisites
No doubt some effects, such as Aharonov-Bohm, came up in undergraduate physics. The best effects, such as this one, increase your understanding in a deep way, like the vector potential is a more fundamental description of the electromagnetic field. While not all effects are this famous, every one of them provided an important lesson in physics at some point in time. In fact, the name of the effect often becomes a proxy for a general concept, as for example Hanbury-Brown and Twiss effect might be used to describe an experiment involving electrons when in fact the original effect arose in stellar interferometry.
Physics6561 Electrodynamics HELP(EXAM HELP, ONLINE TUTOR)
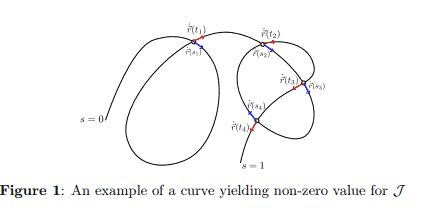
Suppose $\mathbf{r}(s), s \in[0,1]$, is a smooth closed curve in the $x-y$ plane. What are the possible values of the following double integral?
$$
\mathcal{J}=\int_0^1 d s \int_{s^{+}}^1 d t \hat{\mathbf{z}} \cdot \dot{\mathbf{r}}(s) \times \dot{\mathbf{r}}(t) \delta^2(\mathbf{r}(s)-\mathbf{r}(t))
$$
The last factor in the integrand is standard shorthand for the product of two Dirac deltas:
$$
\delta^2(\mathbf{r}(s)-\mathbf{r}(t))=\delta(x(s)-x(t)) \delta(y(s)-y(t))
$$
Delta function forces us to evaluate integrand when $\mathbf{r}(s)=\mathbf{r}(t)$. However integrand $\hat{\mathbf{z}} \cdot \dot{\mathbf{r}}(s) \times \dot{\mathbf{r}}(t)$ yields zero when $\hat{\mathbf{r}}(\mathbf{s})=\hat{\dot{\mathbf{r}}}(\mathbf{t})$, so if we allow $t=s$ the integrand is zero while delta function is non-zero and the integral is not well-defined. Note that this scenario was excluded in the second edition of problem set due to range of $t, t \in(s, 1]$. Thus, the only possibility for finding a non-zero answer is to have points that are intersecting but velocities are not pointing along the same direction, as shown below.
Let’s evaluate integral for these curves. One subtlety is $\delta$-functions are functions of $x(s)-x(t), y(s)-y(t)$, so we need to take into account Jacobian of transformations between $s, t$ and $x(s), x(t)$ (similarly for $y(t), y(s)$ ). To be more concrete, let’s digress for a moment and try to evaluate following integral. First, let’s find the one-dimensional integral:
$$
\begin{gathered}
\int d x \delta(f(x)) g(x) \
f(x)=0 \quad \Rightarrow \quad x=x_0 \
f(x) \approx f\left(x_0\right)+f^{\prime}\left(x_0\right)\left(x-x_0\right)=f^{\prime}\left(x_0\right)\left(x-x_0\right) \
\int d x \delta\left(f^{\prime}\left(x_0\right)\left(x-x_0\right)\right) g(x)=\int d x \frac{\delta\left(x-x_0\right)}{\left|f^{\prime}\left(x_0\right)\right|} g(x)=\frac{g\left(x_0\right)}{\left|f\left(x_0\right)\right|}
\end{gathered}
$$
Now let’s consider a two-dimensional example.
$$
\int d s d t \delta\left(f_1(s, t)\right) \delta\left(f_2(s, t)\right) g(s, t)
$$
Let’s assume $f_1\left(s_0, t_0\right)=0, f_2\left(s_0, t_0\right)=0$, and there is a one-to-one relationships between $(s, t)$ and $\left(f_1, f_2\right)$ in the vicinity of $\left(s_0, t_0\right)$. Then, using change of variables theorem,
$$
\begin{aligned}
& \int d s d t \delta\left(f_1(s, t)\right) \delta\left(f_2(s, t)\right) g(s, t) \
& =\int d f_1 d f_2 \frac{1}{\left|\begin{array}{ll}
\partial_s f_1 & \partial_t f_1 \
\partial_s f_2 & \partial_t f_2
\end{array}\right|} \delta\left(f_1\right) \delta\left(f_2\right) g(s, t)= \
& \left.\frac{g(s, t)}{\left|\begin{array}{ll}
\partial_s f_1 & \partial_t f_1 \
\partial_s f_2 & \partial_t f_2
\end{array}\right|}\right|_{\left(s_0, t_0\right)}=\frac{g\left(s_0, t_0\right)}{\left|\partial_s f_1\left(s_0, t_0\right) \partial_t f_2\left(s_0, t_0\right)-\partial_t f_1\left(s_0, t_0\right) \partial_s f_1\left(s_0, t_0\right)\right|}
\end{aligned}
$$
In an effort to find the simplest shape for a given knotted topology of a loop of string, mathematicians have considered minimizing an energy model where all pairs of line elements $d \mathbf{r}_1$ and $d \mathbf{r}_2$ of the string interact ‘electrostatically’:
$$
d U=\frac{\left|d \mathbf{r}_1\right|\left|d \mathbf{r}_2\right|}{\left|\mathbf{r}_1-\mathbf{r}_2\right|^2}
$$
E\&M was never their strong suit, so we forgive them the exponent 2 in their Coulomb’s law! The total energy has the form of a double integral:
$$
U=\oint d s \oint d t\left(\frac{|\dot{\mathbf{r}}(s)||\dot{\mathbf{r}}(t)|}{|\mathbf{r}(s)-\mathbf{r}(t)|^2}-\frac{1}{(s-t)^2}\right) .
$$
The second term in the integrand, which does not depend on the shape of the knot, is needed to make the expression finite. As physicists we admire the fact that this $U$ is invariant with respect to translations and rotations of the knot. And thanks to that exponent 2, we see that it is even invariant with respect to changes in scale. Show that invariance extends to all elements of the group of conformal transformations by verifying it for Kelvin inversions.
We need to verify that the integrand is invariant under inversions:
$$
\begin{aligned}
\mathbf{r} \rightarrow \mathbf{r}^{\prime} & =\frac{\mathbf{r}}{\mathbf{r} \cdot \mathbf{r}} \
\dot{\mathbf{r}}^{\prime}(t) & =\frac{\dot{\mathbf{r}}(t)}{\mathbf{r}(t) \cdot \mathbf{r}(t)}-\frac{2 \mathbf{r}(t)[\mathbf{r}(t) \cdot \dot{\mathbf{r}}(t)]}{(\mathbf{r}(t) \cdot \mathbf{r}(t))^2} \
\left|\dot{\mathbf{r}}^{\prime}(t)\right|^2 & =\frac{\dot{\mathbf{r}}(t) \cdot \dot{\mathbf{r}}(t)}{(\mathbf{r} \cdot \mathbf{r})^2}+\frac{4(\dot{\mathbf{r}} \cdot \mathbf{r})^2}{(\mathbf{r} \cdot \mathbf{r})^3}-\frac{4(\dot{\mathbf{r}} \cdot \mathbf{r})^2}{(\mathbf{r} \cdot \mathbf{r})^3}=\frac{\dot{\mathbf{r}}(t) \cdot \dot{\mathbf{r}}(t)}{(\mathbf{r} \cdot \mathbf{r})^2}
\end{aligned}
$$
Also for denominator goes as:
$$
\begin{aligned}
& \mathbf{r}(s)-\mathbf{r}(t) \rightarrow \frac{\mathbf{r}(s)}{\mathbf{r}(s) \cdot \mathbf{r}(s)}-\frac{\mathbf{r}(t)}{\mathbf{r}(t) \cdot \mathbf{r}(t)} \
& \Rightarrow \quad|\mathbf{r}(s)-\mathbf{r}(t)|^2 \rightarrow \frac{1}{\mathbf{r}(s) \cdot \mathbf{r}(s)}+\frac{1}{\mathbf{r}(t) \cdot \mathbf{r}(t)}-\frac{2 \mathbf{r}(s) \cdot \mathbf{r}(t)}{\mathbf{r}(t) \cdot \mathbf{r}(t) \mathbf{r}(s) \cdot \mathbf{r}(s)} \
& =\frac{(\mathbf{r}(s)-\mathbf{r}(t))^2}{\mathbf{r}(t) \cdot \mathbf{r}(t) \mathbf{r}(s) \cdot \mathbf{r}(s)}
\end{aligned}
$$
Note that using this equation, we can find again (1.3) by setting $t \rightarrow s+\delta s$ and taking the limit.
Combining these two result, we find invariance of the total energy:
$$
\frac{|\dot{\mathbf{r}}(s)||\dot{\mathbf{r}}(t)|}{|\mathbf{r}(s)-\mathbf{r}(t)|^2} \rightarrow \frac{\frac{|\dot{\mathbf{r}}(s)|}{\mathbf{r}^2(s)} \frac{|\dot{\mathbf{r}}(t)|}{\mathbf{r}^2(t)}}{\frac{\mathbf{r}(s)-\left.\mathbf{r}(t)\right|^2}{\mathbf{r}^2(t) \mathbf{r}^2(s)}}=\frac{|\dot{\mathbf{r}}(s)||\dot{\mathbf{r}}(t)|}{|\mathbf{r}(s)-\mathbf{r}(t)|^2}
$$
Which shows invariance under inversion at origin.

MY-ASSIGNMENTEXPERT™可以为您提供CORNELL.EDU PHYSICS6561 ELECTRODYNAMICS电动力学课程的代写代考和辅导服务!