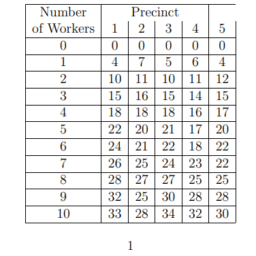
MY-ASSIGNMENTEXPERT™可以为您提供 handbook MTH3330 Operations research运筹学的代写代考和辅导服务!
这是莫纳什大学 运筹学的代写成功案例。

MATH3330课程简介
This unit introduces some of the fundamental methods from operations research and computational mathematics for continuous optimisation problems. A range of such optimisation problems arise in economics, engineering, finance, business, data science and many other application areas. You will receive an introduction to the mathematical theory of continuous optimisation with a focus on linear programming methods and smooth non-linear programming. This will broadly include duality theory, the simplex method for linear programming, network optimisation and iterative methods for unconstrained nonlinear optimisation. You will also learn to implement the computational methods efficiently, how to test their implementations for accuracy and performance, and to interpret the results. You will work on optimisation models for applications in a variety of fields. Applications may include examples of supply chain optimisation, economic modelling (including shadow prices), product mix optimisation, portfolio optimisation, parameter estimation and machine learning.
Prerequisites
Enrolment Rule
keyboard_arrow_down
PREREQUISITE: You must have passed one of MTH2051 or MTH3051 or if you are enrolled in the Bachelor of Applied Data Science MTH2019 or both of (MTH2010 or MTH2015) and (MTH2021 or MTH2025) or if you are enrolled in the Honours of Econometrics, ETC2440 (this requires manual enrolment).
Alternatively you must be enrolled in the Master of Financial Mathematics, the Master of Mathematics, or receive special permission from the unit coordinator.
MTH3330 Operations research HELP(EXAM HELP, ONLINE TUTOR)
ExAmPLE 1.5 Software Creator has to decide how to hire and train programmers over the next four months to complete an ongoing project. The requirements, expressed in terms of the number of programming hours needed, are 8000 in September, 9000 in October, 8000 in November and 6000 in December.
It takes one month of training before a newly recruited programmer can be trained and put to the project. A programmer must be hired a month before working on the actual project. A trainee requires 100 hours of training by experienced programmers during the month of training so that 100 hours less are available from existing trained programmers.
Each experienced programmer can work up to 180 hours in a month, and the company has 50 regular programmers at the beginning of September.
If the maximum time available from experienced programmers exceeds a month’s requirement, they are paid salary for a month.
By the end of each month, $10 \%$ of the experienced programmers quit their jobs to study or for other reasons. The company pays an experienced programmer effectively $₹ 30,000$ per month including other benefits and ₹ 15,000 for a trainee.
Formulate the hiring and training problem as a linear programming problem.
Solution: Let us assume $X_1=$ Number of trainees hired during the month of September
$X_2=$ Number of trainess hired during the month of October
$X_3=$ Number of trainess hired during the month of November.
We do not hire trainees in December because they will be available for January only.
Now
Number of experienced programmers at the beginning of September $e_1=50$
Number of experienced programmers at the beginning of October $e_2=0.9\left(50+X_1\right)$
Number of experienced programmers at the beginning of the month of November $e_3=0.9\left(e_2+X_2\right)$
Number of experienced programmers at the beginning of the month of December $e_4=0.9\left(e_3+X_3\right)$
The objective function is:
Minimize $Z=30,000 \sum_{i=1}^4 e_i+15,000 \sum_{i=1}^3 X_i$
The constraints are:
$$
\begin{aligned}
180 e_1-100 X_1 & \geq 8000 \text { (September) } \
180 e_2-100 X_2 & \geq 9000 \text { (October) } \
150 e_3-100 X_3 & \geq 8000 \text { (November) } \
150 e_4 & \geq 6000 \text { Also, } e_2, e_3, e_4, X_1, X_2, X_3 \geq 0
\end{aligned}
$$
We assume that a programmer becomes trained after one month of training and can leave the organization. We also observe that while the decision variables have to be integers, we are treating them as continuous variables while formulating linear programming problems.
EXAMPLE 1.6 Drink Co., a company manufactures a health drink called “Taste and Strength”. They use five ingredients wheat, milk, nuts, spices and other cereals. They are particular about the amount of starch, carbohydrates and fat contents of the drink. The amount of starch, carbohydrates and starch from ingredient $i$ per $\mathrm{kg}$ is $a_{i 1}, a_{i 2}$ and $a_{i 3}$, respectively. They require a lower and upper limit of $l_j$ and $u_j$ of starch, carbohydrates and fat contents. The cost per $\mathrm{kg}$ of ingredient $i$ is $C_i$. Formulate a linear programming problem to minimize the cost of production of the health drink.
Solution: Let the proportion of ingredient $i$ used in $1 \mathrm{~kg}$ of the health drink be $X_i$. The objective function is:
$$
\text { Minimize } \sum_{i=1}^5 C_i X_i
$$
The constraints are:
Starch
$$
l_1 \leq \sum_{i=1}^5 a_{i 1} X_i \leq u_1
$$
Carbohydrates
$$
\begin{aligned}
& l_2 \leq \sum_{i=1}^5 a_{i 2} X_i \leq u_2 \
& l_3 \leq \sum_{i=1}^5 a_{i 3} X_i \leq u_3 \
& X_i \geq 0
\end{aligned}
$$
ExAMPLE 1.7 Acid Co., a chemical engineering company manufactures two types of acids $A$ and $B$. Both of these involve two chemical operations for each. Each unit of Acid $A$ requires 3 hours on Operation 1 and 4 hours on Operation 2. Each unit of Acid $B$ requires 3 hours on Operation 1 and 2 hours on Operation 2. Available time for Operation 1 is 20 hours and for Operation 2,18 hours. The production of $B$ also results in a by-product $C$ at no extra cost. $A$ part of this by-product can be sold at a profit, but the remainder has to be destroyed.
Acid $A$ sells for $P_1$ rupees profit per unit while Acid $B$ sells for $P_2$ rupees profit per unit. The by-product $C$ can be sold at a unit profit of $P_3$ rupees, and all the unsold quantity must be destroyed; the destruction cost is $P_4$ rupees per unit. Forecasts by sales department show that a maximum of $K$ units of $C$ can be sold; $n$ units of $C$ result for every unit of $B$ produced.
Formulate a linear programme to determine the production quantities of $A$ and $B$, keeping $C$ in mind, so that the total profits will be maximized.
Solution: Let $X_1=$ Amount of Acid $A$ being produced
$$
\begin{aligned}
X_2 & =\text { Amount of Acid } B \text { being produced } \
X_3 & =\text { Amount of by-product sold } \
n X_2 & =\text { Amount of } C \text { produced } \
n X_2-X_3 & =\text { Amount of by-product not sold }
\end{aligned}
$$
The objective function is
$$
\text { Maximize } Z=P_1 X_1+P_2 X_2+P_3 X_3-P_4\left(n X_2-X_3\right)
$$
The constraint equations are
First operation
$$
\begin{array}{lrl}
\text { First operation: } & 3 X_1+4 X_2 & \leq 20 \text { (Capacity constraint) } \
3 X_1+2 X_2 & \leq 18 \text { (Capacity constraint) } \
X_3 & \leq n X_2 \text { (Relationship between } X_3 \text { and } X_2 \text { ) } \
X_3 & \leq K \text { (Sales limit) }
\end{array}
$$
Also
$$
X_1, X_2, X_3 \geq 0
$$

MY-ASSIGNMENTEXPERT™可以为您提供 HANDBOOK MATH3202 OPERATIONS RESEARCH运筹学的代写代考和辅导服务!