如果你也在 怎样代写数理逻辑 Mathematical logic 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。数理逻辑Mathematical logic对数学中形式逻辑的研究。主要子领域包括模型理论、证明理论、集合理论和递归理论。数学逻辑的研究通常涉及形式逻辑系统的数学属性,如其表达或演绎能力。
数理逻辑Mathematical logic在19世纪中期作为数学的一个子领域出现,反映了两个传统的交汇:形式化的哲学逻辑和数学。 “数理逻辑,也被称为’逻辑学’、’符号逻辑’、’逻辑代数’,最近还被简单地称为’形式逻辑’,是在上个世纪过程中借助人工符号和严格的演绎方法阐述的一套逻辑理论。”在这次出现之前,逻辑是与修辞学、计算学、通过三段论和哲学一起研究。20世纪上半叶出现了基本结果的爆发,同时伴随着对数学基础的激烈争论。
数理逻辑Mathematical logic代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的数理逻辑Mathematical logic作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此数理逻辑Mathematical logic作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在数学Mathematics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在数理逻辑Mathematical logic代写方面经验极为丰富,各种数理逻辑Mathematical logic相关的作业也就用不着说。
数学代写|数理逻辑入门代写Introduction To Mathematical logic代考|Introduction and Basic Definitions
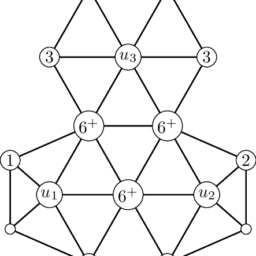
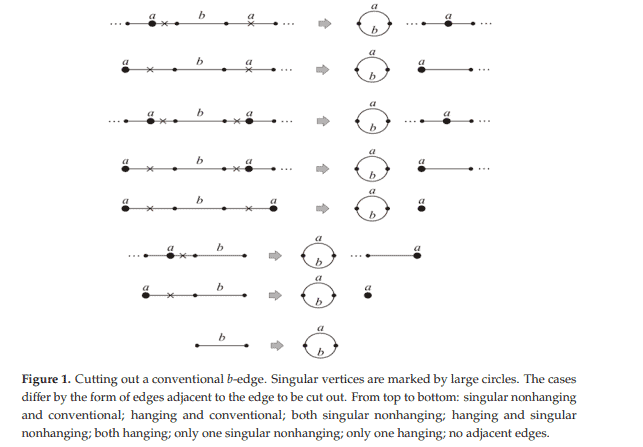
We consider the problem of constructing an algorithm for efficient solution of the below problem. We are given directed graphs $a$ and $b$ in which each vertex has degree either 1 or 2 and each edge is assigned with its unique name, a natural number (in this sense, a graph is referred to as a weighted graph with unique names). We consider a vertex in a graph as two joined (identified) endpoints of the adjacent edges. The following operations over such graphs are well known: cut any vertex (Cut) or join two currently free (i.e., of degree 1) ends (OM); cut a vertex and join one of the thus formed free ends with any currently free end $(S M)$; cut two vertices and join the four thus formed free ends (DM). The latter two operations are compositions of the two former ones, but they are considered as independent operations. These four operations were defined in [1] and are traditionally referred to as $D C J$ (i.e., double cut and join) operations; they were depicted in (Figure 1).
There are two more operations: remove (Rem) a connected fragment of edges with names in $a$ but not in $b$ or, vice versa, insert (Ins) such a fragment with names not in $a$ but in $b$. When removing a fragment, the arising free ends are joined; when inserting a fragment, first, some vertex is cut (if it is not extreme) and, then, after the insertion, two pairs of arising free ends are joined. These operations are analogous to standard deletion of a subword in a word and to insertion of a word as a subword. Each operation is assigned with its cost, a strictly positive rational number.
It is required to find a sequence (composition) of these operations with the minimum total cost which transforms the given graphs a and b, the first into the second. Such a sequence is said to be the shortest. In [2], previously obtained results were stated in detail and references on this problem were presented. Among these references, we point out the two latest papers [3,4], which, in turn, contain further historical references. The previous results concerning this problem and including its applied aspects, were overviewed in [5] (Chapter 10) and [6]. A principal distinction between our Theorem 1 and preceding results is the fact that we do not assume the condition of equal costs of deletion and insertion operations, which essentially simplified the problem. In our paper, we assume no restrictions on costs of these operations. As before, we still keep the condition of equal costs of DCJ operations. Thus, in this paper we prove the following:
Theorem 1. If DCJ operations have the same cost $w$ and the deletion and insertion operations have arbitrary costs $w_d$ and $w_i$, then the Algorithm described below in Section 2, Section 4, and Section 5 outputs an additively shortest sequence of operations and has linear time complexity.
数学代写|数理逻辑入门代写Introduction To Mathematical logic代考|Description of the Algorithm for Case II
We list the stages of this algorithm, which are then explained in sequence and in detail below, in this section (see also Table 1).
Stage 0: Transform initial given graphs $a$ and $b$ into the new graph, denoted by $a+b$ below.
Stage 1.: Cut out conventional edges in $a+b$.
Stage 2.0: Solve the integer linear programming problem which outputs the set of disjoint elements (each of them consisting of pairs, triples, or quadruples of chains of the current graph) with the largest aggregate quality.
Stage 2.1: For each element in this set, perform the interaction between its chains; the interaction is uniquely determined by the element and combines the chains of the element into a single chain.
Stage 3: Circularize chains of sizes strictly larger than 0 into cycles, and then break all cycles into many cycles of size 2; then, remove all singular vertices and loops.
Now, we pass to a detailed description of each stage.
Stage 0: An initial pair of graphs $a$ and $b$ is transformed in linear time into a new («breakpoint») graph $a+b$ such that the original problem is equivalent to the problem of reducing $a+b$ to the simplest form, referred to as final. A final form is a graph consisting of cycles of length 2 (one edge of each cycle is labeled by $a$, and the other, by $b$ ) and isolated conventional vertices; the definition of “conventional» is given below. The proof of the equivalence of these two problems literally repeats the proof of Corollary 5 in [7]; that proof used the equality of costs of DCJ operations only, which is assumed in Theorem 1. In [7], there was also given a linear time algorithm that transforms a solution of the second problem into a solution of the first (and vice versa).
The definition of the graph $a+b$ is given in [7]; in other variants, it was known from earlier works, for instance, from [8,9]. We recall the definition from [7], which describes vertices and edges of $a+b$. Vertices in $a+b$ are all endpoints of edges that occur in both $a$ and $b$ (they are denoted by $n_i$, where $n$ is the edge name, $i=1$ for a tail of an edge, and $i=2$ for its head) and also vertices uniquely corresponding to every maximal connected segment of edges («block») in either $a \backslash b$ or $b \backslash a$, which we label by $a$ or $b$, respectively. Vertices of the first type are referred to as conventional, and those of the second type are referred to as singular. Edges in $a+b$ connect vertices whenever the latter are joined in $a$ or in $b$ or if an extremity of a block is joined with a vertex in $a$ or in $b$; edges are labeled by $a$ or $b$, respectively. Edges of the first type are said to be conventional, and those of the second type are said to be singular. If a singular endpoint in $a+b$ is of degree 1 , then both the edge and the endpoint itself are said to be hanging.

数理逻辑入门代写
数学代写|数理逻辑入门代写Introduction To Mathematical logic代考|Introduction and Basic Definitions
我们考虑构造一个有效求解下列问题的算法。我们给定有向图$a$和$b$,其中每个顶点的度数为1或2,并且每个边都有其唯一的名称,一个自然数(在这种意义上,图被称为具有唯一名称的加权图)。我们认为图中的一个顶点是相邻边的两个连接的(确定的)端点。在这样的图上,下面的操作是众所周知的:切割任意顶点(cut)或连接两个当前自由(即1度)的端点(OM);切割一个顶点,并将由此形成的自由端与任何当前自由端$(S M)$连接;切割两个顶点并连接这样形成的四个自由端(DM)。后两种操作是前两种操作的组合,但它们被认为是独立的操作。这四种操作在[1]中定义,传统上称为$ dcj $(即双切和连接)操作;如图1所示。
还有两种操作:删除(Rem)名称在$a$但不在$b$的连接片段,反之亦然,插入(Ins)这样一个名称不在$a$但在$b$的片段。当移除片段时,产生的自由端连接在一起;当插入一个片段时,首先,一些顶点被切断(如果它不是极端的),然后,在插入之后,两对产生的自由端被连接起来。这些操作类似于在一个词中删除一个子词和插入一个词作为子词。每个操作都有其代价,一个严格的正有理数。
需要找到这些操作的一个序列(组合),用最小的总代价将给定的图a和b,第一个转换为第二个。这样的序列是最短的。文献[2]详细阐述了前人的研究结果,并给出了相关的参考文献。在这些参考文献中,我们指出了两篇最新的论文[3,4],这两篇论文又包含了更多的历史参考文献。文献5和[6]综述了前人关于这一问题及其应用方面的研究成果。我们的定理1和前面的结果之间的一个主要区别是,我们没有假设删除和插入操作的代价相等的条件,这从根本上简化了问题。在本文中,我们假设对这些操作的成本没有限制。和之前一样,我们仍然保持DCJ操作成本相等的条件。因此,本文证明如下:
定理1。如果DCJ操作具有相同的代价$w$,并且删除和插入操作具有任意的代价$w_d$和$w_i$,那么下面第2节、第4节和第5节中描述的算法输出的是一个相加最短的操作序列,并且具有线性时间复杂度。
数学代写|数理逻辑入门代写Introduction To Mathematical logic代考|Description of the Algorithm for Case II
我们列出了该算法的各个阶段,然后在本节中依次详细解释(参见表1)。
阶段0:将初始给定图$a$和$b$转换为新的图,用下面的$a+b$表示。
阶段1。:剪掉$a+ $ b的常规边缘。
阶段2.0:求解输出聚合质量最大的不相交元素集合(每个不相交元素由当前图的链对、三元组或四元组组成)的整数线性规划问题。
阶段2.1:对于集合中的每个元素,执行其链之间的交互;交互作用由元素唯一地决定,并将元素的链组合成单个链。
阶段3:将大小严格大于0的链循环成循环,然后将所有循环分解成许多大小为2的循环;然后,移除所有奇异顶点和循环。
现在,我们对每个阶段进行详细的描述。
阶段0:在线性时间内将一对初始图$a$和$b$转换为一个新的(«断点»)图$a+b$,使得原始问题等同于将$a+b$简化为最简单形式的问题,称为最终形式。最后一种形式是由长度为2的循环(每个循环的一条边标记为$ A $,另一条标记为$b$)和孤立的常规顶点组成的图;“常规”的定义如下。这两个问题等价性的证明实际上重复了[7]中推论5的证明;证明只使用了DCJ操作的代价相等,这在定理1中是假设的。文献[7]中也给出了一种线性时间算法,将第二个问题的解转化为第一个问题的解(反之亦然)。
图$a+b$的定义如[7]所示;在其他版本中,它是从早期的作品中得知的,例如[8,9]。我们回想一下[7]中的定义,它描述了$a+b$的顶点和边。$a+b$中的顶点是在$a$和$b$中出现的所有边的端点(它们用$n_i$表示,其中$n$是边的名称,$i=1$表示一条边的尾部,$i=2$表示它的头部),也是唯一对应于$a \反斜杠b$或$b \反斜杠a$中的每个最大连接边段(«块»)的顶点,我们分别用$a$或$b$标记。第一种类型的顶点被称为常规顶点,第二种类型的顶点被称为奇异顶点。$a+b$中的边连接在$a$或$b$中连接的顶点,或者如果一个块的端点与$a$或$b$中的顶点连接;边分别用$a$或$b$标记。第一种类型的边被称为约定边,而第二种类型的边被称为奇异边。如果$a+b$中的奇异端点是1次,那么这条边和端点本身都被称为挂起。

数学代写|数理逻辑入门代写Introduction To Mathematical logic代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。