如果你也在 怎样代写图论Graph Theory 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。图论Graph Theory在数学和计算机科学领域,图论是对图的研究,涉及边和顶点之间的关系。它是一门热门学科,在计算机科学、信息技术、生物科学、数学和语言学中都有应用。
图论Graph Theory在数学和计算机科学领域,图论是对图的研究,涉及边和顶点之间的关系。它是一门热门学科,在计算机科学、信息技术、生物科学、数学和语言学中都有应用。近年来,图论已经成为各种学科的重要数学工具,从运筹学和化学到遗传学和语言学,从电气工程和地理到社会学和建筑。同时,它本身也作为一门有价值的数学学科出现。
my-assignmentexpert™图论Graph Theory代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的图论Graph Theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此图论Graph Theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在网课代修方面已经树立了自己的口碑, 保证靠谱, 高质且原创的网课代写服务。我们的专家在图论Graph Theory代写方面经验极为丰富,各种图论Graph Theory相关的作业也就用不着 说。
我们提供的图论Graph Theory MATH334及其相关学科的代写,服务范围广, 其中包括但不限于:
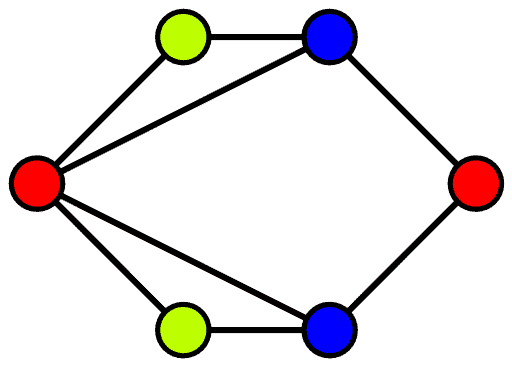
数学代写|图论代写Graph Theory代写|Colouring vertices
How do we determine the chromatic number of a given graph? How can we find a vertex-colouring with as few colours as possible? How does the chromatic number relate to other graph invariants, such as average degree, connectivity or girth?
Straight from the definition of the chromatic number we may derive the following upper bound:
Proposition 5.2.1. Every graph $G$ with $m$ edges satisfies
$$
\chi(G) \leqslant \frac{1}{2}+\sqrt{2 m+\frac{1}{4}} .
$$
Proof. Let $c$ be a vertex colouring of $G$ with $k=\chi(G)$ colours. Then $G$ has at least one edge between any two colour classes: if not, we could have used the same colour for both classes. Thus, $m \geqslant \frac{1}{2} k(k-1)$. Solving this inequality for $k$, we obtain the assertion claimed.
One obvious way to colour a graph $G$ with not too many colours is the following greedy algorithm: starting from a fixed vertex enumeration $v_1, \ldots, v_n$ of $G$, we consider the vertices in turn and colour each $v_i$ with the first available colour-e.g., with the smallest positive integer not already used to colour any neighbour of $v_i$ among $v_1, \ldots, v_{i-1}$. In this way, we never use more than $\Delta(G)+1$ colours, even for unfavourable choices of the enumeration $v_1, \ldots, v_n$. If $G$ is complete or an odd cycle, then this is even best possible.
数学代写|图论代写Graph Theory代写|Colouring edges
Clearly, every graph $G$ satisfies $\chi^{\prime}(G) \geqslant \Delta(G)$. For bipartite graphs, we have equality here:
Proposition 5.3.1. (König 1916)
Every bipartite graph $G$ satisfies $\chi^{\prime}(G)=\Delta(G)$.
Proof. We apply induction on $|G|$. For $|G|=0$ the assertion holds.
Now assume that $|G| \geqslant 1$, and that the assertion holds for graphs with fewer edges. Let $\Delta:=\Delta(G)$, pick an edge $x y \in G$, and choose a $\Delta$ edge-colouring of $G-x y$ by the induction hypothesis. Let us refer to the edges coloured $\alpha$ as $\alpha$-edges, etc.
In $G-x y$, each of $x$ and $y$ is incident with at most $\Delta-1$ edges. Hence there are $\alpha, \beta \in{1, \ldots, \Delta}$ such that $x$ is not incident with an $\Delta, x y$ $\alpha$-edge and $y$ is not incident with a $\beta$-edge. If $\alpha=\beta$, we can colour the edge $x y$ with this colour and are done; so we may assume that $\alpha \neq \beta$, and that $x$ is incident with a $\beta$-edge.
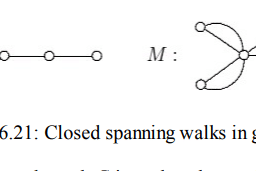
Let us extend this edge to a maximal walk $W$ from $x$ whose edges are coloured $\beta$ and $\alpha$ alternately. Since no such walk contains a vertex twice (why not?), $W$ exists and is a path. Moreover, $W$ does not contain $y$ : if it did, it would end in $y$ on an $\alpha$-edge (by the choice of $\beta$ ) and thus have even length, so $W+x y$ would be an odd cycle in $G$ (cf. Proposition 1.6.1). We now recolour all the edges on $W$, swapping $\alpha$ with $\beta$. By the choice of $\alpha$ and the maximality of $W$, adjacent edges of $G-x y$ are still coloured differently. We have thus found a $\Delta$-edge-colouring of $G-x y$ in which neither $x$ nor $y$ is incident with a $\beta$-edge. Colouring $x y$ with $\beta$, we extend this colouring to a $\Delta$-edge-colouring of $G$.
Theorem 5.3.2. (Vizing 1964)
Every graph $G$ satisfies
$$
\Delta(G) \leqslant \chi^{\prime}(G) \leqslant \Delta(G)+1 .
$$
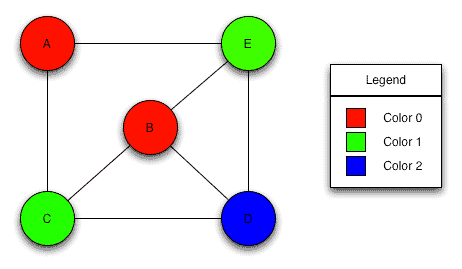
图论代写
数学代写|图论代写Graph Theory代写|Colouring vertices
平面图形$G$最显著的特征之一是它的面循环,即约束面的循环。如果$G$是2连接的,那么它就被它的面部循环所覆盖,所以在某种意义上,这些形成了一个“大”集。事实上,面部循环的集合很大,甚至在它们产生整个循环空间的意义上:$G$中的每个循环很容易被看作是面部循环的总和(见下文)。另一方面,面部循环只“薄”覆盖$G$,因为每条边缘最多位于其中两条。在本节中,我们的第一个目的是要证明这样一个庞大而稀疏分布的循环族的存在不仅是平面性的一个显著特征,而且是它的核心:它是平面性的特征。
设$G=(V, E)$为任意图形。我们称其边空间$\mathcal{E}(G)$的子集$\mathcal{F}$为简单,如果$G$的每条边最多位于两个$\mathcal{F}$集合中。例如,切割空间$\mathcal{C}^*(G)$有一个简单的基础:根据命题1.9.3,它是由给定顶点$v$上的所有边形成的切割$E(v)$产生的,并且一条边$x y \in G$只在$v=x$和$v=y$上位于$E(v)$。
定理4.5.1。(麦克莱恩1937)
一个图是平面的当且仅当它的循环空间有一个简单基。
证明。这个断言对于阶数最多为2的图是微不足道的,我们考虑阶数至少为3的图$G$。如果$\kappa(G) \leqslant 1$,则$G$是两个适当诱导子图$G_1, G_2$与$\left|G_1 \cap G_2\right| \leqslant 1$的并集。那么$\mathcal{C}(G)$是$\mathcal{C}\left(G_1\right)$和$\mathcal{C}\left(G_2\right)$的直接和,因此有一个简单的基础当且仅当$\mathcal{C}\left(G_1\right)$和$\mathcal{C}\left(G_2\right)$都是(证明?)此外,$G$是平面的当且仅当$G_1$和$G_2$都是平面的:这不仅是由库拉托夫斯基定理得出的,而且也是由简单的几何考虑得出的。因此,$G$的断言归纳地遵循$G_1$和$G_2$的断言。对于剩下的证明,我们现在假设$G$是2连通的。
数学代写|图论代写Graph Theory代写|Colouring edges
显然,每个图$G$都满足$\chi^{\prime}(G) \geqslant \Delta(G)$。对于二部图,我们有等式:
提案5.3.1。(König 1916)
每个二部图$G$满足$\chi^{\prime}(G)=\Delta(G)$。
证明。我们对$|G|$应用归纳法。对于$|G|=0$,该断言成立。
现在假设$|G| \geqslant 1$,并且该断言适用于具有较少边的图。设$\Delta:=\Delta(G)$,选取一条边$x y \in G$,并根据归纳假设选择一条$\Delta$边着色的$G-x y$。让我们把颜色为$\alpha$的边称为$\alpha$边,等等。
在$G-x y$中,每个$x$和$y$最多与$\Delta-1$条边相关。因此,存在$\alpha, \beta \in{1, \ldots, \Delta}$,使得$x$与$\Delta, x y$$\alpha$ -edge不关联,$y$与$\beta$ -edge不关联。如果$\alpha=\beta$,我们可以用这种颜色给边缘$x y$上色,这样就完成了;所以我们可以假设$\alpha \neq \beta$,并且$x$与$\beta$ -边重合。
让我们把这条边延伸到从$x$开始的最大步行$W$,它的边交替用$\beta$和$\alpha$的颜色表示。因为没有这样的行走包含一个顶点两次(为什么不呢?),$W$存在并且是一条路径。此外,$W$不包含$y$:如果它包含,它将以$y$结束于一条$\alpha$ -边(通过选择$\beta$),因此具有偶数长度,因此$W+x y$将是$G$中的奇循环(参见命题1.6.1)。现在我们将$W$上的所有边重新上色,将$\alpha$与$\beta$交换。通过选择$\alpha$和$W$的最大值,$G-x y$的相邻边仍然是不同的颜色。因此,我们发现了$G-x y$的$\Delta$ -边着色,其中$x$和$y$都与$\beta$ -边无关。用$\beta$对$x y$进行着色,我们将这种着色扩展为$G$的$\Delta$边着色。
定理5.3.2。(Vizing 1964)
每个图$G$都满足
$$
\Delta(G) \leqslant \chi^{\prime}(G) \leqslant \Delta(G)+1 .
$$

数学代写|图论代写Graph Theory代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。