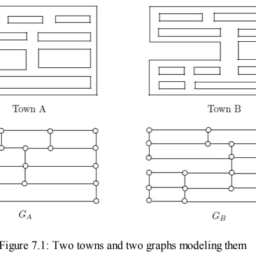
如果你也在 怎样代写图论Graph Theory 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。图论Graph Theory有趣的部分原因在于,图可以用来对某些问题中的情况进行建模。这些问题可以在图表的帮助下进行研究(并可能得到解决)。因此,图形模型在本书中经常出现。然而,图论是数学的一个领域,因此涉及数学思想的研究-概念和它们之间的联系。我们选择包含的主题和结果是因为我们认为它们有趣、重要和/或代表主题。
图论Graph Theory通过熟悉许多过去和现在对图论的发展负责的人,可以增强对图论的欣赏。因此,我们收录了一些关于“图论人士”的有趣评论。因为我们相信这些人是图论故事的一部分,所以我们在文中讨论了他们,而不仅仅是作为脚注。我们常常没有认识到数学是一门有生命的学科。图论是人类创造的,是一门仍在不断发展的学科。
my-assignmentexpert™图论Graph Theory代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的图论Graph Theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此图论Graph Theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在网课代修方面已经树立了自己的口碑, 保证靠谱, 高质且原创的网课代写服务。我们的专家在图论Graph Theory代写方面经验极为丰富,各种图论Graph Theory相关的作业也就用不着 说.
数学代写|图论代写Graph Theory代写|Mader’s theorem
In analogy to Menger’s theorem we may consider the following question: given a graph $G$ with an induced subgraph $H$, up to how many independent $H$-paths can we find in $G$ ?
In this section, we present without proof a deep theorem of Mader, which solves the above problem in a fashion similar to Menger’s theorem. Again, the theorem says that an upper bound on the number of such paths that arises naturally from the size of certain separators is indeed attained by some suitable set of paths.
What could such an upper bound look like? Clearly, if $X \subseteq V(G-H)$ and $F \subseteq E(G-H)$ are such that every $H$-path in $G$ has a vertex or an edge in $X \cup F$, then $G$ cannot contain more than $|X \cup F|$ independent $H$-paths. Hence, the least cardinality of such a set $X \cup F$ is a natural upper bound for the maximum number of independent $H$-paths. (Note that every $H$-path meets $G-H$, because $H$ is induced in $G$ and edges of $H$ do not count as $H$-paths.)
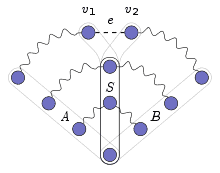
In contrast to Menger’s theorem, this bound can still be improved. The minimality of $|X \cup F|$ implies that no edge in $F$ has an end in $X$ : otherwise this edge would not be needed in the separator. Let $Y:=$ $V(G-H) \backslash X$, and denote by $\mathcal{C}_F$ the set of components of the graph $(Y, F)$. Since every $H$-path avoiding $X$ contains an edge from $F$, it has at least two vertices in $\partial C$ for some $C \in \mathcal{C}F$, where $\partial C$ denotes the set of vertices in $C$ with a neighbour in $G-X-C$ (Fig. 3.4.1). The number of independent $H$-paths in $G$ is therefore bounded above by $$ M_G(H):=\min \left(|X|+\sum{C \in \mathcal{C}_F}\left\lfloor\frac{1}{2}|\partial C|\right\rfloor\right),
$$
where the minimum is taken over all $X$ and $F$ as described above: $X \subseteq$ $V(G-H)$ and $F \subseteq E(G-H-X)$ such that every $H$-path in $G$ has a vertex or an edge in $X \cup F$.
数学代写|图论代写Graph Theory代写|Linking pairs of vertices
Let $G$ be a graph, and let $X \subseteq V(G)$ be a set of vertices. We call $X$ linked in $G$ if whenever we pick distinct vertices $s_1, \ldots, s_{\ell}, t_1, \ldots, t_{\ell}$ in $X$ we can find disjoint paths $P_1, \ldots, P_{\ell}$ in $G$ such that each $P_i$ links $s_i$ to $t_i$ and has no inner vertex in $X$. Thus, unlike in Menger’s theorem, we are not merely asking for disjoint paths between two sets of vertices: we insist that each of these paths shall link a specified pair of endvertices.
If $|G| \geqslant 2 k$ and every set of at most $2 k$ vertices is linked in $G$, then $G$ is $k$-linked. As is easily checked, this is equivalent to requiring that disjoint paths $P_i=s_i \ldots t_i$ exist for every choice of exactly $2 k$ vertices $s_1, \ldots, s_k, t_1, \ldots, t_k$. In practice, the latter is easier to prove, because we need not worry about inner vertices in $X$.
Clearly, every $k$-linked graph is $k$-connected. The converse, however, seems far from true: being $k$-linked is clearly a much stronger property than $k$-connectedness. Still, we shall prove in this section that we can force a graph to be $k$-linked by assuming that it is $f(k)$-connected, for some function $f: \mathbb{N} \rightarrow \mathbb{N}$. We first give a nice and simple proof that such a function $f$ exists at all. In the remainder of the section we then prove that $f$ can even be chosen linear.
The basic idea in the simple proof is as follows. If we can prove that $G$ contains a subdivision $K$ of a large complete graph, we can use Menger’s theorem to link the vertices of $X$ disjointly to branch vertices of $K$, and then hope to pair them up as desired through the subdivided edges of $K$. This requires, of course, that our paths do not hit too many of the subdivided edges before reaching the branch vertices of $K$.
图论代写
数学代写|图论代写Graph Theory代写|Mader’s theorem
与门格尔定理类似,我们可以考虑以下问题:给定一个图$G$和一个诱导子图$H$,在$G$中我们最多可以找到多少个独立的$H$路径?
在本节中,我们提出了一个没有证明的Mader的深度定理,它以类似于门格尔定理的方式解决了上述问题。同样,这个定理说,这样的路径数目的上界是由某些分隔符的大小自然产生的,确实是由一些合适的路径集达到的。
这样的上界是什么样的呢?显然,如果$X \subseteq V(G-H)$和$F \subseteq E(G-H)$是这样的,$G$中的每个$H$ -path在$X \cup F$中都有一个顶点或一条边,那么$G$不能包含超过$|X \cup F|$独立的$H$ -path。因此,这样一个集合$X \cup F$的最小基数是独立$H$ -路径的最大数目的自然上界。(请注意,每个$H$ -path都满足$G-H$,因为$H$在$G$中被诱导,并且$H$的边不算作$H$ -paths。)
与门格尔定理相反,这个界仍然可以改进。$|X \cup F|$的最小值意味着$F$中没有一条边在$X$中结束:否则分隔符中将不需要这条边。设$Y:=$$V(G-H) \backslash X$,用$\mathcal{C}_F$表示图$(Y, F)$的分量集。由于避开$X$的每个$H$ -path都包含一条来自$F$的边,因此对于某些$C \in \mathcal{C}F$,它在$\partial C$中至少有两个顶点,其中$\partial C$表示$C$中有一个邻居在$G-X-C$中的顶点集(图3.4.1)。因此,$G$中独立的$H$ -路径的数量以$$ M_G(H):=\min \left(|X|+\sum{C \in \mathcal{C}_F}\left\lfloor\frac{1}{2}|\partial C|\right\rfloor\right),
$$为界
其中最小值被取到所有$X$和$F$,如上所述:$X \subseteq$$V(G-H)$和$F \subseteq E(G-H-X)$,使得$G$中的每个$H$ -path在$X \cup F$中都有一个顶点或一条边。
数学代写|图论代写Graph Theory代写|Linking pairs of vertices
设$G$是一个图,$X \subseteq V(G)$是一组顶点。我们称$X$链接在$G$如果我们在$X$中选择不同的顶点$s_1, \ldots, s_{\ell}, t_1, \ldots, t_{\ell}$,我们可以在$G$中找到不相交的路径$P_1, \ldots, P_{\ell}$,使得每个$P_i$将$s_i$链接到$t_i$并且在$X$中没有内部顶点。因此,与门格尔定理不同的是,我们不仅仅要求两个顶点集之间的不相交路径:我们坚持这些路径中的每一个都必须连接一个指定的端点对。
如果$|G| \geqslant 2 k$和最多$2 k$个顶点的集合在$G$中链接,那么$G$是$k$链接的。很容易检查,这相当于要求不相交的路径$P_i=s_i \ldots t_i$存在于每个恰好$2 k$顶点$s_1, \ldots, s_k, t_1, \ldots, t_k$的选择。在实践中,后者更容易证明,因为我们不需要担心$X$中的内部顶点。
显然,每个$k$连接的图都是$k$连接的。然而,相反的情况似乎远非如此:与$k$相连显然比与$k$相连强得多。尽管如此,我们将在本节中证明,对于某些函数$f: \mathbb{N} \rightarrow \mathbb{N}$,我们可以通过假设一个图是$f(k)$连接的来强制它是$k$连接的。我们首先给出一个漂亮而简单的证明,证明这样的函数$f$存在。在本节的其余部分,我们将证明$f$甚至可以被选为线性的。
简单证明的基本思想如下。如果我们能证明$G$包含一个大的完全图的细分$K$,我们可以使用门格尔定理将$X$的顶点与$K$的分支顶点不联合地连接起来,然后希望通过$K$的细分边将它们按需要配对。当然,这要求我们的路径在到达$K$的分支顶点之前不会碰到太多的细分边。