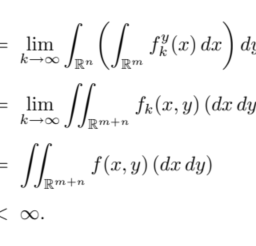如果你也在 怎样代写实分析real analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。实分析real analysis是数学分析的一个分支,研究实数、实数序列和实数函数的行为。 实分析研究的实值序列和函数的一些特殊性质包括收敛性、极限、连续性、平稳性、可微分性和可整定性。实分析有别于复分析,后者涉及复数及其函数的研究。
实分析real analysis是数学中的一个经典分支,它的发展是为了使数和函数的研究正规化,并研究重要的概念,如极限和连续性。这些概念是微积分及其应用的基础。实物分析已经成为许多应用领域中不可或缺的工具。
实分析real analysis的基础知识:序列和数列的收敛性、连续性、可分性、黎曼积分、函数的序列和数列、均匀性以及极限操作的互换。
my-assignmentexpert™ 实分析real analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的实分析real analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此复分析complex analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学mathematics代写服务。我们的专家在实分析real analysis代写方面经验极为丰富,各种实分析real analysis相关的作业也就用不着 说。
我们提供的实分析real analysis及其相关学科的代写,服务范围广, 其中包括但不限于:
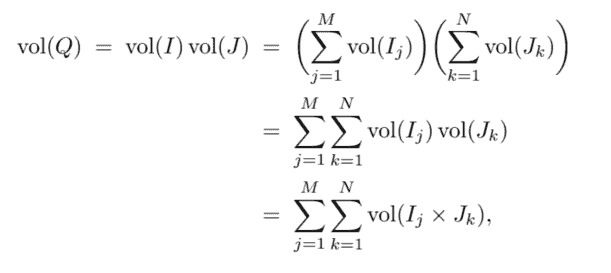
数学代写|实分析代写real analysis代考|Boxes
We begin with some especially simple sets whose volumes are known. These are intervals in one dimension, rectangles in two dimensions, and rectangular parallelepipeds in higher dimensions. In fact, we will restrict to rectangular parallelepipeds whose sides are parallel to the coordinate axes. For simplicity, we refer to these sets as “boxes.” Here is the precise definition of a box and its volume.
Definition 2.1.1 (Boxes).
(a) A box in $\mathbb{R}^{d}$ is a Cartesian product of $d$ finite closed intervals. In other words, a box is a set of the form
$$
Q=\left[a_{1}, b_{1}\right] \times \cdots \times\left[a_{d}, b_{d}\right]=\prod_{j=1}^{d}\left[a_{j}, b_{j}\right]
$$
where $a_{j}<b_{j}$ for each $j$.
(b) The volume of the box $Q$ defined in equation (2.1) is the product of the lengths of its sides:
$$
\operatorname{vol}(Q)=\left(b_{1}-a_{1}\right) \cdots\left(b_{d}-a_{d}\right)=\prod_{j=1}^{d}\left(b_{j}-a_{j}\right)
$$
(c) The interior of the box $Q$ is the Cartesian product
$$
Q^{\circ}=\left(a_{1}, b_{1}\right) \times \cdots \times\left(a_{d}, b_{d}\right)=\prod_{j=1}^{d}\left(a_{j}, b_{j}\right)
$$
and the boundary of $Q$ is $\partial Q=Q \backslash Q^{\circ}$.
数学代写|实分析代写REAL ANALYSIS代考|Some Facts about Boxes
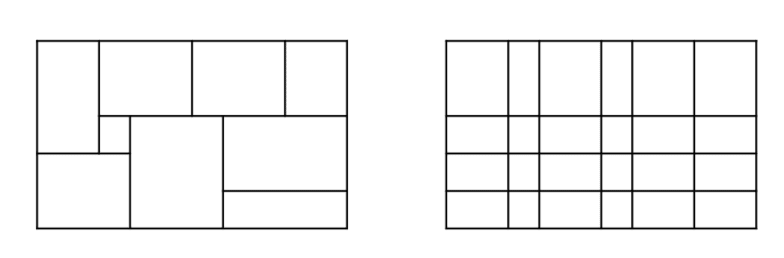
Every open subset of $\mathbb{R}$ can be written as a union of at most countably many disjoint open intervals. Bounded open intervals in $\mathbb{R}$ are one-dimensional open balls, so every bounded open subset of $\mathbb{R}$ can be written as a union of at most countably many disjoint open balls. This fact does not generalize to higher dimensions. For example, the open square $S=(0,1)^{2}$ in $\mathbb{R}^{2}$ cannot be written as a union of countably many disjoint open balls.
Although we cannot write open sets as disjoint unions of balls in general, the following lemma provides us with a useful substitute. According to this lemma, every open set in $\mathbb{R}^{d}$, in any dimension $d \geq 1$, can be written as a union of countably many nonoverlapping cubes. Two easy examples in one dimension (where cubes are simply finite closed intervals) are
$$
\mathbb{R}=\bigcup_{k \in \mathbb{Z}}[k, k+1] \quad \text { and } \quad(0, \infty)=\bigcup_{k \in \mathbb{Z}}\left[2^{k}, 2^{k+1}\right]
$$
Since any finite union of cubes is a compact set, there is no way that we can write an open set as a union of finitely many cubes. On the other hand, the next lemma shows that we will never need more than countably many cubes.
数学代写|实分析代写real analysis代考|Exterior Lebesgue Measure
Now we turn from boxes to generic subsets of $\mathbb{R}^{d}$. In order to define the measure of a set $E \subseteq \mathbb{R}^{d}$, we will try to approximate it by boxes. Suppose that we cover $E$ by some countable collection of boxes $\left{Q_{k}\right}$, so we have
$$
E \subseteq \bigcup_{k} Q_{k}
$$
We have not yet assigned a measure to either of $E$ or $\cup Q_{k}$, but whatever those measures are, it seems reasonable to expect that the measure of $\cup Q_{k}$ should be at least as large as the measure of $E$. Additionally, it seems reasonable that the measure of a union of boxes should be no more than the sum of the volumes of the boxes $Q_{k}$. The measure of the union could be smaller than the sum of the volumes due to overlaps, but we should at least have an inequality. Hence, whatever we decide that the measure of $E$ should be, if we let $|E|_{e}$ denote that measure then we should have
$$
|E|{e} \leq \sum{k} \operatorname{vol}\left(Q_{k}\right)
$$
Thus, each covering of $E$ by boxes gives us an upper bound for the measure of $E$. Some coverings may be “better” than others in some sense, but instead of worrying about how to quantify “better,” we will simply take every possible covering into account and declare that the exterior measure of $E$ is the infimum of $\sum \operatorname{vol}\left(Q_{k}\right)$ over every countable covering of $E$ by boxes (we restrict our attention to coverings by countably many boxes because each box has a strictly positive volume). This leads us to the following definition.
实分析代写
数学代写|实分析代写REAL ANALYSIS代考|BOXES
我们从一些体积已知的特别简单的集合开始。这些是一维的间隔,二维的矩形和更高维度的长方体。事实上,我们将限制为边平行于坐标轴的长方体。为简单起见,我们将这些集合称为“盒子”。这是一个盒子和它的体积的精确定义。
定义 2.1.1乙这X和s.
一种一个盒子在Rd是笛卡尔积d有限闭区间。换句话说,一个盒子是一组表格
问=[一种1,b1]×⋯×[一种d,bd]=∏j=1d[一种j,bj]
在哪里一种j<bj对于每个j.
b盒子的体积问在等式中定义2.1是其边长的乘积:
卷(问)=(b1−一种1)⋯(bd−一种d)=∏j=1d(bj−一种j)
C盒子的内部问是笛卡尔积
问∘=(一种1,b1)×⋯×(一种d,bd)=∏j=1d(一种j,bj)
和的边界问是∂问=问∖问∘.
数学代写|实分析代写REAL ANALYSIS代考|SOME FACTS ABOUT BOXES
的每个开放子集R可以写成最多可数个不相交开区间的并集。有界开区间R是一维开球,所以每个有界开子集R最多可以写成多个不相交的空球的并集。这个事实不能推广到更高的维度。例如,开放广场小号=(0,1)2在R2不能写成可数许多不相交的空心球的并集。
虽然我们一般不能将开集写成球的不相交并集,但以下引理为我们提供了一个有用的替代方案。根据这个引理,每个开集在Rd, 在任何维度d≥1, 可以写成多个不重叠立方体的并集。一维中的两个简单示例在H和r和C你b和s一种r和s一世米p一世是F一世n一世吨和C一世这s和d一世n吨和rv一种一世s是
R=⋃到∈从[到,到+1] 和 (0,∞)=⋃到∈从[2到,2到+1]
由于任何有限立方的并集都是紧集,我们无法将开集写成有限多个立方的并集。另一方面,下一个引理表明我们永远不需要超过可数个立方体。
数学代写|实分析代写REAL ANALYSIS代考|EXTERIOR LEBESGUE MEASURE
现在我们从盒子转向通用子集Rd. 为了定义集合的度量和⊆Rd,我们将尝试通过框来近似它。假设我们覆盖和通过一些可数的盒子集合\left{Q_{k}\right}\left{Q_{k}\right},所以我们有
和⊆⋃到问到
我们尚未为其中任何一个指定措施和或者∪问到, 但无论这些措施是什么, 预期的措施似乎是合理的∪问到应该至少与测量的一样大和. 此外,盒子并集的度量不应超过盒子体积的总和似乎是合理的问到. 由于重叠,联合的度量可能小于体积的总和,但我们至少应该有一个不等式。因此,无论我们决定和应该是,如果我们让|和|和表示那个度量那么我们应该有
$$
| E | {e} \ leq \ sum {k} \ operatorname {vol} \ leftQ_{k}\对Q_{k}\对
$$
因此,每个覆盖和by box 为我们提供了测量的上限和. 有些覆盖物在某种意义上可能比其他覆盖物“更好”,但与其担心如何量化“更好”,我们将简单地考虑所有可能的覆盖物,并声明和是下确界∑卷(问到)在每个可数覆盖上和按盒子在和r和s吨r一世C吨这你r一种吨吨和n吨一世这n吨这C这v和r一世nGsb是C这你n吨一种b一世是米一种n是b这X和sb和C一种你s和和一种CHb这XH一种s一种s吨r一世C吨一世是p这s一世吨一世v和v这一世你米和. 这导致我们得出以下定义。

数学代写|实分析代写real analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
离散数学代写
Partial Differential Equations代写可以参考一份偏微分方程midterm答案解析