如果你也在 怎样代写微分方程differential equation这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。微分方程differential equation在数学中,是将一个或多个未知函数及其导数联系起来的方程。在应用中,函数通常代表物理量,导数代表其变化率,而微分方程则定义了两者之间的关系。这种关系很常见;因此,微分方程在许多学科,包括工程、物理学、经济学和生物学中发挥着突出作用。
微分方程differential equation研究主要包括研究其解(满足每个方程的函数集合),以及研究其解的性质。只有最简单的微分方程可以用明确的公式求解;然而,一个给定的微分方程的解的许多属性可以在不精确计算的情况下确定。
my-assignmentexpert™ 微分方程differential equation作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的微分方程differential equation作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微分方程differential equation作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的微分方程differential equation代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种微分方程differential equation相关的作业也就用不着 说。
我们提供的微分方程differential equation及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|微分方程代写differential equation代考|Volterra integro-differential
If in the equations studied, there are both derivative and integral terms of the unknown functions, the equations are referred to as integro-differential equations. In this section, Volterra integro-differential equations with separable variables are discussed.
Definition 4.2. The mathematical form of a first-order Volterra integro-differential equation is given by
$$
x^{\prime}(t)=f(t, x(t))+\int_{0}^{t} K(s, t, x(s)) \mathrm{d} s
$$
Volterra integro-differential equation is named after an Italian mathematician Vito Volterra (1860-1940). In [18], some numerical algorithms are presented for solving certain Volterra integro-differential equations, but the accuracy is not very high.Similarly, the mathematical definition of high-order Volterra integro-differential equations may also be presented. In fact, through effective transforms, a certain class
of Volterra integro-differential equations can be converted into ordinary differential equations or delay differential equations. For instance, if the kernel $K(s, t, x(s))$ in the integral can be factored into a product of functions of $t$ and $s$, that is,
$$
K(s, t, \chi(s))=K_{1}(t) K_{2}(s, \chi(s)),
$$
the original equation can be rewritten as
$$
x^{\prime}(t)=f(t, x(t))+K_{1}(t) \int_{0}^{t} K_{2}(s, x(s)) \mathrm{d} s .
$$
Taking derivatives with respect to $t$ of both sides of (4.5.1) yields
$$
x^{\prime \prime}(t)=f^{\prime}(t, x(t))+K_{1}(t) K_{2}^{\prime}(t, \chi(t))+K_{1}^{\prime}(t) \int_{0}^{t} K_{2}(s, \chi(s)) \mathrm{d} s .
$$
It can be seen that in (4.5.3) and (4.5.4), the same integral term appears. Thus it can be eliminated simply by substituting one equation into another, and the original integro-differential equation can be converted into an ordinary differential equation, so that numerical solvers can be used to study the original integro-differential equations. In this section, the combined method is demonstrated through examples to solve some Volterra integro-differential equations.
数学代写|微分方程代写differential equation代考|simple Volterra integro-differential equation
Let us consider a simple Volterra integro-differential equation ${ }^{[18]}$
$$
x^{\prime}(t)=1-\int_{0}^{t} x(s) \mathrm{d} s
$$
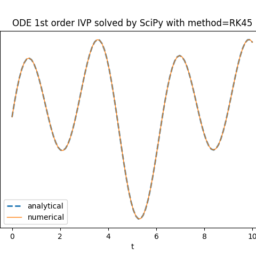
with given initial value $\chi(0)=0$. It is known that the analytical solution is $\chi(t)=\sin t$. Convert it into an ordinary differential equation.
Solutions. For this simple problem, the manual method can be used directly to find the solution. Substituting $t$ into the equation, it is found that $x^{\prime}(0)=1$. Taking derivatives of both sides with respect to $t$, it is seen that
$$
x^{\prime \prime}(t)=-x(t)
$$
with initial values $x(0)=0$ and $x^{\prime}(0)=1$. The differential equation has, in fact, multiple analytical solution expressions, namely $x(t)=\sin (2 k \pi+t)$, where $k$ is an integer. The solution provided, $x(t)=\sin t$, is merely one of them.
微分方程代写
数学代写|微分方程代写DIFFERENTIAL EQUATION代考|VOLTERRA INTEGRO-DIFFERENTIAL
如果在所研究的方程中,存在未知函数的导数和积分项,则这些方程称为积分-微分方程。在本节中,讨论了具有可分离变量的 Volterra 积分微分方程。
定义 4.2。一阶沃尔泰拉积分微分方程的数学形式由下式给出
X′(吨)=F(吨,X(吨))+∫0吨到(s,吨,X(s))ds
沃尔泰拉积分-微分方程以意大利数学家维托沃尔泰拉命名1860−1940. 在18,提出了一些求解某些Volterra积分-微分方程的数值算法,但精度不是很高。同样,也可以给出高阶Volterra积分-微分方程的数学定义。事实上,通过有效的变换,某个类
Volterra 的积分-微分方程可以转化为常微分方程或延迟微分方程。例如,如果内核到(s,吨,X(s))在积分中可以分解为函数的乘积吨和s, 那是,
到(s,吨,χ(s))=到1(吨)到2(s,χ(s)),
原方程可以改写为
X′(吨)=F(吨,X(吨))+到1(吨)∫0吨到2(s,X(s))ds.
取导数吨的双方4.5.1产量
X′′(吨)=F′(吨,X(吨))+到1(吨)到2′(吨,χ(吨))+到1′(吨)∫0吨到2(s,χ(s))ds.
可以看出,在4.5.3和4.5.4,同样的积分项出现。这样就可以简单地将一个方程代入另一个方程来消除它,并将原来的积分微分方程转化为一个常微分方程,从而可以使用数值求解器来研究原来的积分微分方程。在本节中,通过示例演示了组合方法来求解一些 Volterra 积分-微分方程。
数学代写|微分方程代写DIFFERENTIAL EQUATION代考|SIMPLE VOLTERRA INTEGRO-DIFFERENTIAL EQUATION
让我们考虑一个简单的 Volterra 积分微分方程[18]
X′(吨)=1−∫0吨X(s)ds
具有给定的初始值χ(0)=0. 已知解析解为χ(吨)=没有吨. 将其转化为常微分方程。
解决方案。对于这个简单的问题,可以直接使用手动的方法来寻找解决方案。替代吨代入方程,发现X′(0)=1. 对两边取导数吨, 可以看出
X′′(吨)=−X(吨)
具有初始值X(0)=0和X′(0)=1. 微分方程实际上有多个解析解表达式,即X(吨)=没有(2到圆周率+吨), 在哪里到是一个整数。提供的解决方案,X(吨)=没有吨, 只是其中之一。

数学代写|微分方程代写differential equation代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。