如果你也在 怎样代写复杂网络complex networks这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。复杂网络complex networks在网络理论的背景下,是一种具有非微观拓扑特征的图(网络)–这些特征在简单的网络(如格子或随机图)中不会出现,但在代表真实系统的网络中经常出现。复杂网络的研究是一个年轻而活跃的科学研究领域(自2000年以来),主要受到现实世界网络的经验发现的启发,如计算机网络、生物网络、技术网络、大脑网络、气候网络和社会网络。
复杂网络complex networks有两类众所周知且研究较多的复杂网络是无标度网络和小世界网络,它们的发现和定义是该领域的典型案例研究。两者都具有特定的结构特征–前者是幂律学位分布,后者是短路径长度和高聚类。然而,随着复杂网络研究的重要性和受欢迎程度不断提高,网络结构的许多其他方面也引起了人们的注意。
my-assignmentexpert™ 复杂网络complex networks作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的复杂网络complex networks作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此复杂网络complex networks作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的复杂网络complex networks代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种复杂网络complex networks相关的作业也就用不着 说。
我们提供的复杂网络complex networks及其相关学科的代写,服务范围广, 其中包括但不限于:
非线性方法 nonlinear method functional analysis
变分法 Calculus of Variations
数学代写|复杂网络作业代写complex networks代考|Mixing by Vertex Degree
We will spend the rest of this article examining one particular case of mixing according to a scalar vertex property, that of mixing by vertex degree, which has been studied for some time in the social networks literature and has recently attracted attention in the mathematical and physical literature also. Krapivsky and Redner $[27]$ for instance found in studies of the preferential attachment model of Barabási and Albert [6] that edges did not fall between vertices independent of their degrees. Instead there was a higher probability to find some
80 M.E.J. Newman and M. Girvan
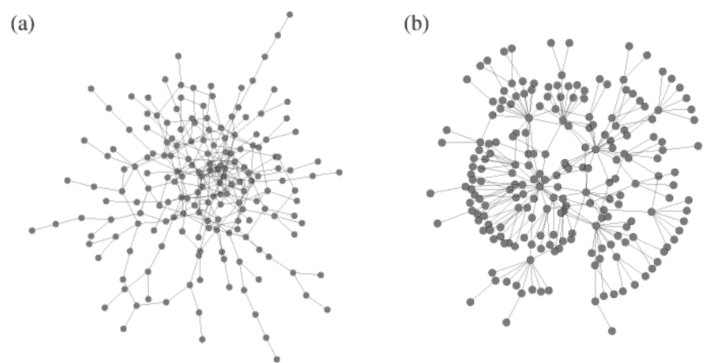
degree combinations at the ends of edges than others. Pastor-Satorras et al. [40] subsequently showed for data on the structure of the Internet at the level of autonomous systems that the degrees of adjacent vertices were anticorrelated, i.e., that high-degree vertices prefer to attach to low-degree vertices, rather than other high-degree ones – the network is disassortative by degree. To demonstrate this, they measured the mean degree degree $\left\langle k_{\mathrm{nn}}\right\rangle$ of the nearest-neighbours of a vertex, as a function of that vertex’s degree $k$. They found that $\left\langle k_{\mathrm{nn}}\right\rangle$ decreases with increasing $k$, approximately as $k^{-1 / 2}$. That is, the mean degree of your neighbours goes down as yours goes up. Maslov and Sneppen [29] have offered an explanation of this result in terms of ensembles of graphs in which double edges between vertices are forbidden. Maslov and Sneppen also showed in a separate paper $[30]$ that the protein interaction network of the yeast $S$. Cerevisiae displays a similar sort of disassortative mixing.
An alternative way to quantify assortative mixing by degree in a network is to use an assortativity coefficient of the type described in the previous section [35]. Let us define $e_{j k}$ to be the fraction of edges in a network that connect a vertex of degree $j$ to a vertex of degree $k$. (As before, if the ends of an edge connect different types of vertices, then the matrix will be asymmetric, otherwise it will be symmetric.) In fact, we define $j$ and $k$ to be the “excess degrees” of the two vertices, i.e., the number of edges incident on them less the one edge that we are looking at at present. In other words, $j$ and $k$ are one less than the total degrees of the two vertices. This designation turns out to be mathematically convenient for many developments. If the degree distribution of the network as a whole is $p_{k}$, then the distribution of the excess degree of the vertex at the end of a randomly chosen edge is
$$
q_{k}=\frac{(k+1) p_{k+1}}{z}
$$
where $z=\sum_{k} k p_{k}$ is the mean degree [37]. Then one can define the assortativity coefficient to be
$$
r=\frac{\sum_{j k} j k\left(e_{j k}-q_{j} q_{k}\right)}{\sigma_{q}^{2}},
$$
where $\sigma_{q}$ is the standard deviation of the distribution $q_{k}$. On a directed or similar network, where the ends of an edge are not the same and $e_{j k}$ is asymmetric, this generalizes to
$$
r=\frac{\sum_{j k} j k\left(e_{j k}-q_{j}^{a} q_{k}^{b}\right)}{\sigma_{a} \sigma_{b}}
$$
复杂网络代写
数学代写|复杂网络作业代写COMPLEX NETWORKS代考|MIXING BY VERTEX DEGREE
我们将在本文的其余部分研究一个根据标量顶点属性进行混合的特殊情况,即按顶点度数进行混合,这已经在社交网络文献中研究了一段时间,并且最近在数学和物理领域引起了关注。文学也。克拉皮夫斯基和雷德纳[27]例如,在对 Barabási 和 Albert 的优先依恋模型的研究中发现6边缘没有落在与度数无关的顶点之间。相反,在边缘的末端找到大约
80 个 MEJ Newman 和 M. Girvan度数组合的概率高于其他组合。
牧师-萨托拉斯等人。40随后在自治系统级别显示有关互联网结构的数据,相邻顶点的度数是反相关的,即高度顶点更喜欢连接到度低的顶点,而不是其他高度顶点 -网络在程度上是不相称的。为了证明这一点,他们测量了平均度数⟨ķnn⟩一个顶点的最近邻,作为该顶点度数的函数ķ. 他们发现⟨ķnn⟩随着增加而减少ķ, 大约为ķ−1/2. 也就是说,你的邻居的平均程度随着你的上升而下降。马斯洛夫和斯内彭29已经根据图的集合提供了对该结果的解释,其中顶点之间的双边是被禁止的。马斯洛夫和斯内彭也在另一篇论文中展示[30]酵母的蛋白质相互作用网络小号. 酿酒酵母显示出类似的不相配混合。
在网络中按程度量化分类混合的另一种方法是使用上一节中描述的类型的分类系数35. 让我们定义和jķ是网络中连接度数顶点的边的分数j到度数的顶点ķ. 一种sb和F这r和,一世F吨H和和nds这F一种n和dG和C这nn和C吨d一世FF和r和n吨吨是p和s这F在和r吨一世C和s,吨H和n吨H和米一种吨r一世X在一世llb和一种s是米米和吨r一世C,这吨H和r在一世s和一世吨在一世llb和s是米米和吨r一世C.事实上,我们定义j和ķ是两个顶点的“过度度数”,即入射在它们上的边数减去我们目前正在查看的边数。换句话说,j和ķ比两个顶点的总度数小一。事实证明,这种指定在数学上对许多开发来说是方便的。如果整个网络的度分布为pķ,则在随机选择的边的末端,顶点的过度度分布为
qķ=(ķ+1)pķ+1和
在哪里和=∑ķķpķ是平均度数37. 然后可以将分类系数定义为
r=∑jķjķ(和jķ−qjqķ)σq2,
在哪里σq是分布的标准差qķ. 在有向或类似网络上,边的端点不相同,并且和jķ是不对称的,这可以推广到
r=∑jķjķ(和jķ−qj一种qķb)σ一种σb

数学代写|复杂网络作业代写complex networks代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。