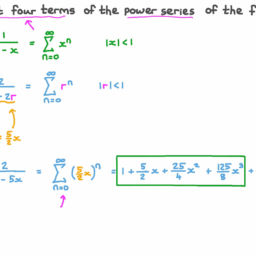
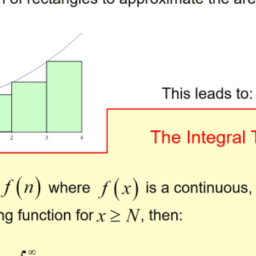
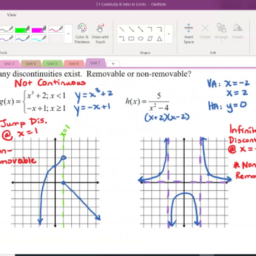
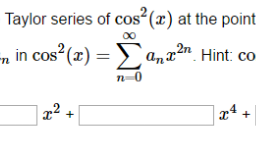| Be sure you understand why $\sum_{k-1}^{m+1} x_{k}=\sum_{k=1}^{m} x_{k}+x_{m+1}$. As a slight generalization of this notation, $$ \sum_{j=k}^{m} x_{j} \equiv x_{k}+\cdots+x_{m} $$ It is also possible to change the variable of summation. $$ \sum_{j=1}^{m} x_{j}=x_{1}+x_{2}+\cdots+x_{m} $$ while if $r$ is an integer, the notation requires $$ \sum_{j=1+r}^{m+r} x_{j} $$ and so $\sum_{j-1}^{m} x_{j}=\sum_{j-1+r}^{m+r} x_{j}-r .$ Summation notation will be used throughout the book whenever it is convenient to do so. Example 2.1.13 Add the fractions, $\frac{x}{x^{2}+y}+\frac{y}{x-1}$. You add these just like they were numbers. Write the first expression as $\frac{x(z-1)}{\left(z^{2}+y\right)(x-1)}$ and the second as $\frac{y\left(z^{2}+y\right)}{(x-1)\left(x^{2}+y\right)}$. Then since these have the same common denominator, you add them as follows. $$ \frac{x}{x^{2}+y}+\frac{y}{x-1}=\frac{x(x-1)}{\left(x^{2}+y\right)(x-1)}+\frac{y\left(x^{2}+y\right)}{(x-1)\left(x^{2}+y\right)}=\frac{x^{2}-x+y x^{2}+y^{2}}{\left(x^{2}+y\right)(x-1)} $$ $2.2$ Exercises Consider the expression $x+y(x+y)-x(y-x) \equiv f(x, y)$. Find $f(-1,2)$. Show $-(a b)=(-a) b$. Show on the number line the effect of multiplying a number by $-1$. Add the fractions $\frac{x}{x^{2}-1}+\frac{x-1}{x+1}$. Find a formula for $(x+y)^{2},(x+y)^{3}$, and $(x+y)^{4}$. Based on what you observe for these, give a formula for $(x+y)^{8}$. When is it true that $(x+y)^{n}=x^{n}+y^{n}$ ? Find the error in the following argument. Let $x=y=1$. Then $x y=y^{2}$ and so $x y-x^{2}=y^{2}-x^{2}$. Therefore, $x(y-x)=(y-x)(y+x)$. Dividing both sides by $(y-x)$ yields $x=x+y$. Now substituting in what these variables equal yields $1=1+1$. Find the error in the following argument. $\sqrt{x^{2}+1}=x+1$ and so letting $x=2$, $\sqrt{5}=3$. Therefore, $5=9$. Find the error in the following. Let $x=1$ and $y=2$. Then $\frac{1}{3}=\frac{1}{x+y}=\frac{1}{x}+\frac{1}{y}=$ $1+\frac{1}{2}=\frac{3}{2}$. Then cross multiplying, yields $2=9$. Find the error in the following argument. Let $x=3$ and $y=1$. Then $1=3-2=$ $3-(3-1)=x-y(x-y)=(x-y)(x-y)=2^{2}=4 .$Find the error in the following. $\frac{x y+y}{x}=y+y=2 y$. Now let $x=2$ and $y=2$ to obtain $3=4$. Show the rational numbers satisfy the field axioms. You may assume the associative, commutative, and distributive laws hold for the integers. Show that for $n$ a positive integer, $\sum_{k=0}^{n}(a+b k)=\sum_{k-0}^{n}(a+b(n-k))$. Explain why $$ \begin{gathered} 2 \sum_{k=0}^{n}(a+b k)=\sum_{k=0}^{n} 2 a+b n=(n+1)(2 a+b n) \ \text { and } \operatorname{so} \sum_{k=0}^{n}(a+b k)=(n+1) \frac{a+(a+b n)}{2} . \end{gathered} $$ $2.3$ Set Notation A set is just a collection of things called elements. Often these are also referred to as points in calculus. For example ${1,2,3,8}$ would be a set consisting of the elements $1,2,3$, and 8 . To indicate that 3 is an element of ${1,2,3,8}$, it is customary to write $3 \in{1,2,3,8} .9 \notin{1,2,3,8}$ means 9 is not an element of ${1,2,3,8}$. Sometimes a rule specifies a set. For example you could specify a set as all integers larger than 2. This would be written as $S={x \in \mathbb{Z}: x>2}$. This notation says: the set of all integers, $x$, such that $x>2$. If $A$ and $B$ are sets with the property that every element of $A$ is an element of $B$, then $A$ is a subset of $B$. For example, ${1,2,3,8}$ is a subset of ${1,2,3,4,5,8}$, in symbols, ${1,2,3,8} \subseteq{1,2,3,4,5,8}$. The same statement about the two sets may also be written as ${1,2,3,4,5,8} \supseteq{1,2,3,8}$. The union of two sets is the set consisting of everything which is contained in at least one of the sets, $A$ or $B$. As an example of the union of two sets, ${1,2,3,8} \cup{3,4,7,8}=$ ${1,2,3,4,7,8}$ because these numbers are those which are in at least one of the two sets. In general $$ A \cup B \equiv{x: x \in A \text { or } x \in B} $$ Be sure you understand that something which is in both $A$ and $B$ is in the union. It is not an exclusive or. The intersection of two sets, $A$ and $B$ consists of everything which is in both of the sets. Thus ${1,2,3,8} \cap{3,4,7,8}={3,8}$ because 3 and 8 are those elements the two sets have in common. In general, $$ A \cap B \equiv{x: x \in A \text { and } x \in B} . $$ When with real numbers, $[a, b]$ denotes the set of real numbers $x$, such that $a \leq x \leq b$ and $[a, b)$ denotes the set of real numbers such that $a \leq x<b .(a, b)$ consists of the set of real numbers, $x$ such that $a<x<b$ and $(a, b]$ indicates the set of numbers, $x$ such that $a<x \leq b .[a, \infty)$ means the set of all numbers, $x$ such that $x \geq a$ and $(-\infty, a]$ means the set of all real numbers which are less than or equal to $a$. These sorts of sets of real numbers are called intervals. The two points, $a$ and $b$ are called endpoints of the interval. Other intervals such as $(-\infty, b)$ are defined by analogy to what was just explained. In general, the curved parenthesis indicates the end point it sits next to is not included while the square parenthesis indicates this end point is included. The reason that there will always be a curved parenthesis next to $\infty$ or $-\infty$ is that these are not real numbers. Therefore, they cannot be included in any set of real numbers. It is assumed that the reader is already familiar with order which is discussed in the next section more carefully. The emphasis here is on the geometric significance of these intervals. That is $[a, b)$ consists of all points of the number line which are to the right |

real analysis代写analysis 2, analysis 3请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
代写
隐藏