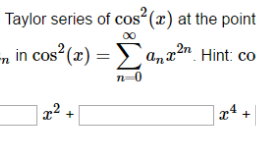9.8 Fubini’s Theorem an Introduction
Fubini’s theorem has become the name of a theorem which involves interchanging the order of integration in iterated integrals. You may have seen it mentioned in a beginning calculus course. It is actually an incredibly deep result, much more so than what will be indicated here. Here I will only consider enough to allow what will be done in this book. It turns out that iterated integrals are what occur naturally in many situations, and each integral in an iterated integral is a one dimensional notion, so it is natural to consider the interchange of iterated integrals in a book on single variable calculus. All of this depends on the theorems about continuous functions defined on a subset of $F^{p}$. In the case considered here, $p=2$.
The following theorem is just like an earlier one for functions of one variable.
206
CHAPTER 9. INTEGRATION
Theorem $9.8 .1$ Let $f$ be increasing and let $g$ be continuous on $[a, b]$. Then there exists $c \in[a, b]$ such that
$$
\int_{a}^{b} g d f=g(c)(f(b)-f(c))
$$
Proof: If $f$ is constant, there is nothing to prove so assume $f(b)>f(a)$. Let $M \equiv \max {g(x): x \in[a, b]}, m \equiv \min {g(x): x \in[a, b]}$. Then in a Riemann sum for $\int_{a}^{b} g d f$, if $g$ is replaced by $M$, the resulting Riemann sum will increase and if it is replaced with $m$, the resulting sum will decrease. Therefore,
$$
m(f(b)-f(a))=\int_{a}^{b} m d f \leq \int_{a}^{b} g d f \leq \int_{a}^{b} M d f=M(f(b)-f(a))
$$
and so $m \leq \frac{1}{f(b)-f(a)} \int_{a}^{b} g d f \leq M$. Therefore, by the intermediate value theorem, there is $c \in[a, b]$ such that $\frac{1}{f(b)-f(a)} \int_{a}^{b} g d f=g(c)$.

Lemma 9.8.2 Let $f:[a, b] \times[c, d] \rightarrow \mathbb{R}$ be continuous at every point so it is uniformly continuous. Let $\alpha, \beta$ be increasing on $[a, b],[c, d]$ respectively. Then
$$
x \rightarrow \int_{c}^{d} f(x, y) d \beta(y), y \rightarrow \int_{a}^{b} f(x, y) d \alpha(x)
$$
are both continuous functions.
Proof: Consider the first. The other is exactly similar.
$$
\begin{aligned}
\mid \int_{c}^{d} f(x, y) d \beta(y)-& \int_{c}^{d} f(\hat{x}, y) d \beta(y)|=| \int_{c}^{d}(f(x, y)-f(\hat{x}, y)) d \beta(y) \mid \
& \leq \int_{c}^{d}|f(x, y)-f(\hat{x}, y)| d \beta(y)
\end{aligned}
$$
But by uniform continuity, if $|x-\hat{x}|$ is small enough, then the integrand
$$
|f(x, y)-f(\hat{x}, y)|<\varepsilon
$$
and so the integral in the above is no larger than $\varepsilon(\beta(d)-\beta(c))$. Since $\varepsilon$ is arbitrary, this shows the claim.

Note that, since these are continuous functions, it follows from Theorem $9.3 .7$ that it makes perfect sense to write the iterated integrals
$$
\int_{a}^{b} \int_{c}^{d} f(x, y) d \beta(y) d \alpha(x), \int_{c}^{d} \int_{a}^{b} f(x, y) d \alpha(x) d \beta(y)
$$
Of course the burning question is whether these two numbers are equal. This is the next theorem.
$$
\int_{a}^{b} \int_{c}^{d} f(x, y) d \beta(y) d \alpha(x), \int_{c}^{d} \int_{a}^{b} f(x, y) d \alpha(x) d \beta(y)
$$
Of course the burning question is whether these two numbers are equal. This is the next theorem.

Theorem 9.8.3 Let $f:[a, b] \times[c, d] \rightarrow \mathbb{R}$ be continuous and let $\beta, \alpha$ be increasing functions on $[c, d],[a, b]$ respectively. Then
$$
\int_{a}^{b} \int_{c}^{d} f(x, y) d \beta(y) d \alpha(x)=\int_{c}^{d} \int_{a}^{b} f(x, y) d \alpha(x) d \beta(y)
$$
Proof:
$$
\int_{a}^{b} \int_{c}^{d} f(x, y) d \beta(y) d \alpha(x)=\sum_{i=1}^{n} \int_{x_{i-1}}^{x_{1}} \int_{c}^{d} f(x, y) d \beta(y) d \alpha(x)
$$
207
9.8. FUBINI’S THEOREM AN INTRODUCTION
$$
\begin{aligned}
&=\sum_{i=1}^{n} \int_{x_{i-1}}^{x_{i}} \sum_{j=1}^{m} \int_{y_{j-1}}^{y_{j}} f(x, y) d \beta(y) d \alpha(x) \
&=\sum_{i=1}^{n} \sum_{j=1}^{m} \int_{x_{i-1}}^{x_{i}} \int_{y_{j-1}}^{y_{j}} f(x, y) d \beta(y) d \alpha(x)
\end{aligned}
$$
By the mean value theorem for integrals, Theorem $9.8 .1$
$$
\begin{aligned}
&=\sum_{i=1}^{n} \sum_{j=1}^{m} \int_{x_{1-1}}^{x_{i}}\left(\beta\left(y_{j}\right)-\beta\left(y_{j-1}\right)\right) f\left(x, t_{j}\right) d \alpha(x) \
&=\sum_{i=1}^{n} \sum_{j=1}^{m}\left(\beta\left(y_{j}\right)-\beta\left(y_{j-1}\right)\right)\left(\alpha\left(x_{i}\right)-\alpha\left(x_{i-1}\right)\right) f\left(s_{i}, t_{j}\right)
\end{aligned}
$$
Also, by the same reasoning,
$$
\begin{aligned}
& \int_{c}^{d} \int_{a}^{b} f(x, y) d \alpha(x) d \beta(y) \
=& \sum_{j=1}^{m} \sum_{i=1}^{n}\left(\beta\left(y_{j}\right)-\beta\left(y_{j-1}\right)\right)\left(\alpha\left(x_{i}\right)-\alpha\left(x_{i-1}\right)\right) f\left(s_{i}^{\prime}, t_{j}^{\prime}\right)
\end{aligned}
$$
and now because of uniform continuity, it follows that if the partition points are close enough,
$$
\left|f\left(s_{j}^{\prime}, t_{j}^{\prime}\right)-f\left(s_{j}, t_{j}\right)\right|<\frac{\varepsilon}{(\beta(d)-\beta(c))(\alpha(b)-\alpha(a))}
$$
and so
$$
\left|\int_{c}^{d} \int_{a}^{b} f(x, y) d \alpha(x) d \beta(y)-\int_{c}^{d} \int_{a}^{b} f(x, y) d \alpha(x) d \beta(y)\right|<\varepsilon
$$
Since $\varepsilon$ is arbitrary, this shows the two iterated integrals are equal.
The following is concerning a very important formula. First recall the arctan function. Restricting tan to $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$, this function is one to one and has an inverse function called arctan. Thus arctan $(y)=x$ where $x \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$ and $\tan x=y$. Then, using the theory of the derivative of inverse functions, it follows that arctan is differentiable and
$$
\arctan ^{\prime}(y) y^{\prime}(x)=1
$$

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

抽象代数Galois理论代写

偏微分方程代写成功案例

代数数论代考

组合数学代考

统计作业代写

集合论数理逻辑代写案例

凸优化代写

统计exam代考