微积分note The Nested Interval Lemma

In Russia there is a kind of doll called a matrushka doll. You pick it up and notice it comes apart in the center. Separating the two halves you find an identical doll inside. Then you notice this inside doll also comes apart in the center. Separating the two halves, you find yet another identical doll inside. This goes on quite a while until the final doll is in one piece. The nested interval lemma is like a matrushka doll except the process never stops. It involves a sequence of intervals, the first containing the second, the second containing the third, the third containing the fourth and so on. The fundamental question is whether there exists a point in all the intervals. Sometimes there is such a point and this comes from completeness.

Lemma 4.6.1 Let $I_{k}=\left[a^{k}, b^{k}\right]$ and suppose that for all $k=1,2, \cdots, I_{k} \supseteq I_{k+1}$. Then there exists a point, $c \in \mathbb{R}$ which is an element of every $I_{k}$. If the diameters (length) of these intervals, denoted as diam $\left(I_{k}\right)$ converges to 0 , then there is a unique point in the intersection of all these intervals.
Proof: Since $I_{k} \supseteq I_{k+1}$, this implies
Consequently, if $k \leq l$,
$$
a^{l} \leq a^{l} \leq b^{l} \leq b^{k}
$$
Now define
$$
c \equiv \sup \left{a^{l}: l=1,2, \cdots\right}
$$
By the first inequality in $4.6$, and $4.7$
$$
a^{k} \leq c=\sup \left{a^{l}: l=k, k+1, \cdots\right} \leq b^{k}
$$
for each $k=1,2 \ldots$. Thus $c \in I_{k}$ for every $k$ and this proves the lemma. The reason for the last inequality in $4.8$ is that from $4.7, b^{k}$ is an upper bound to $\left{a^{l}: l=k, k+1, \cdots\right}$. Therefore, it is at least as large as the least upper bound.

For the last claim, suppose there are two points $x, y$ in the intersection. Then $|x-y|=r>0$ but eventually the diameter of $I_{k}$ is less than $r$. Thus it cannot contain both $x$ and $y$.

This is really quite a remarkable result and may not seem so obvious. Consider the intervals $I_{k} \equiv(0,1 / k)$. Then there is no point which lies in all these intervals because no negative number can be in all the intervals and $1 / k$ is smaller than a given positive number whenever $k$ is large enough. Thus the only candidate for being in all the intervals is 0 and 0 has been left out of them all. The problem here is that the endpoints of the intervals were not included, contrary to the hypotheses of the above lemma in which all the intervals included the endpoints.

Corollary 4.6.2 Let $R_{n} \equiv \prod_{k=1}^{p}\left[a_{k}^{n}, b_{k}^{n}\right]$ where $R_{n+1} \subseteq R_{n}$. Then $\cap_{n=1}^{\infty} R_{n} \neq \emptyset .$ If the diameter of $R_{n}$ defined as $\max \left{b_{k}^{n}-a_{k}^{n}: k \leq p\right}$ converges to 0, then there is exactly one point in this intersection.

Proof: Since these rectangles $R_{k}$ are nested, it follows that $\left[a_{k}^{n}, b_{k}^{n}\right] \supseteq\left[a_{k}^{n+1}, b_{k}^{n+1}\right]$ and so there exists $x_{k} \in \cap_{n}\left[a_{k}^{n}, b_{k}^{n}\right]$. Then $x \equiv\left(x_{1}, \cdots, x_{p}\right) \in \cap_{n} R_{n}$. In case the diameter of $R_{n}$ converges to 0, if $x, y \in \cap R_{n}$, then $|x-y| \leq \max \left{b_{k}^{n}-a_{k}^{n}, k \leq p\right}$ and this converges to 0 as $n \rightarrow \infty$. Thus $x=y$.

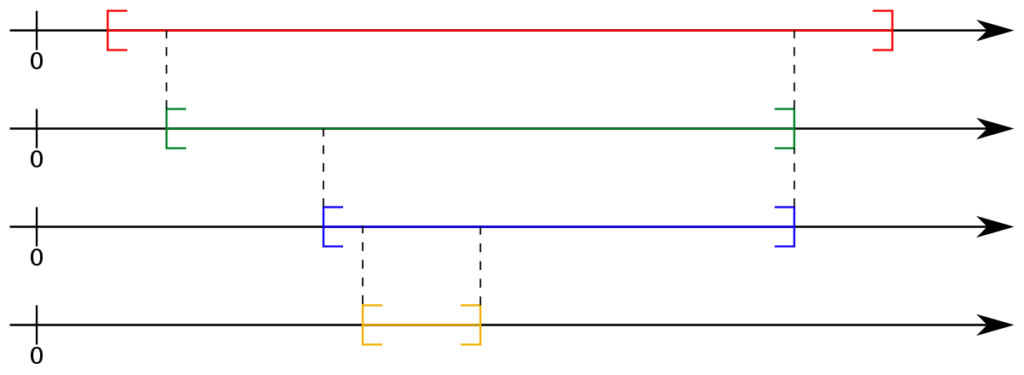
在俄罗斯有一种娃娃，叫做 matrushka 娃娃。你把它捡起来，发现它在中间分开了。将两半分开，您会发现里面有一个相同的娃娃。然后你注意到这个里面的娃娃也在中间分开了。将两半分开，你会发现里面还有另一个相同的娃娃。这持续了很长一段时间，直到最后的娃娃合二为一。嵌套的区间引理就像一个 matrushka 娃娃，只是这个过程永远不会停止。它涉及一系列间隔，第一个包含第二个，第二个包含第三个，第三个包含第四个，依此类推。基本问题是在所有区间中是否存在一个点。有时有这样一个观点，这来自于完整性。

引理 4.6.1 令 $I_{k}=\left[a^{k}, b^{k}\right]$ 并假设对于所有 $k=1,2, \cdots, I_{k} \supseteq我{k+1}$。那么存在一个点，$c \in \mathbb{R}$，它是每个 $I{k}$ 的一个元素。如果这些区间的直径（长度），表示为 diam $\left(I_{k}\right)$ 收敛到 0 ，那么在所有这些区间的交点中存在一个唯一点。
证明：由于 $I_{k} \supseteq I_{k+1}$，这意味着
因此，如果 $k \leq l$，
$$
a^{l} \leq a^{l} \leq b^{l} \leq b^{k}
$$
现在定义
$$
c \equiv \sup \left{a^{l}: l=1,2, \cdots\right}
$$
通过 $4.6$ 和 $4.7$ 中的第一个不等式
$$
a^{k} \leq c=\sup \left{a^{l}: l=k, k+1, \cdots\right} \leq b^{k}
$$
对于每个 $k=1,2 \ldots$。因此，对于每个 $k$，$c \in I_{k}$ 就证明了引理。 $4.8$ 中最后一个不等式的原因是，从 $4.7 开始，b^{k}$ 是 $\left{a^{l} 的上界：l=k, k+1, \cdots\right}美元。因此，它至少与最小上限一样大。

对于最后一个声明，假设交点中有两个点 $x, y$。然后 $|x-y|=r>0$ 但最终 $I_{k}$ 的直径小于 $r$。因此它不能同时包含 $x$ 和 $y$。

这确实是一个非常了不起的结果，可能看起来并不那么明显。考虑区间 $I_{k} \equiv(0,1 / k)$。那么在所有这些区间中就没有一点，因为在所有区间中都没有负数，并且只要 $k$ 足够大，$1 / k$ 就会小于给定的正数。因此，在所有区间中的唯一候选者是 0，而 0 已被排除在所有区间之外。这里的问题是不包括区间的端点，这与上述引理的假设相反，其中所有区间都包括端点。

推论 4.6.2 令 $R_{n} \equiv \prod_{k=1}^{p}\left[a_{k}^{n}, b_{k}^{n}\right]$ 其中 $R_ {n+1} \subseteq R_{n}$。那么 $\cap_{n=1}^{\infty} R_{n} \neq \emptyset .$ 如果 $R_{n}$ 的直径定义为 $\max \left{b_{k}^{n }-a_{k}^{n}：k \leq p\right}$ 收敛到0，那么这个交点正好有一个点。

证明：由于这些矩形 $R_{k}$ 是嵌套的，因此 $\left[a_{k}^{n}, b_{k}^{n}\right] \supseteq\left[a_{k} ^{n+1}, b_{k}^{n+1}\right]$ 等存在 $x_{k} \in \cap_{n}\left[a_{k}^{n}, b_ {k}^{n}\right]$。然后 $x \equiv\left(x_{1}, \cdots, x_{p}\right) \in \cap_{n} R_{n}$。如果$R_{n}$的直径收敛于0，如果$x, y \in \cap R_{n}$, 那么$|x-y| \leq \max \left{b_{k}^{n}-a_{k}^{n}, k \leq p\right}$ 并且这收敛到 0 作为 $n \rightarrow \infty$。因此$x=y$。