统计代写| Hypergeometric stat代写
统计代考
3.4 Hypergeometric
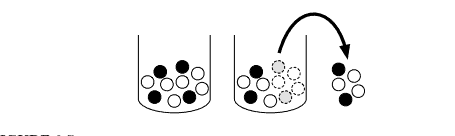
If we have an urn filled with $w$ white and $b$ black balls, then drawing $n$ balls out of the urn with replacement yields a $\operatorname{Bin}(n, w /(w+b))$ distribution for the number of white balls obtained in $n$ trials, since the draws are independent Bernoulli trials, each with probability $w /(w+b)$ of success. If we instead sample without replacement, as illustrated in Figure 3.7, then the number of white balls follows a Hypergeometric distribution.
Story 3.4.1 (Hypergeometric distribution). Consider an urn with $w$ white balls and $b$ black balls. We draw $n$ balls out of the urn at random without replacement, such that all $\left(\begin{array}{c}w+b \ n\end{array}\right)$ samples are equally likely. Let $X$ be the number of white balls in the sample. Then $X$ is said to have the Hypergeometric distribution with parameters $w, b$, and $n$; we denote this by $X \sim \operatorname{HGeom}(w, b, n)$.
116
FIGURE $3.7$
Hypergeometric story. An urn contains $w=6$ white balls and $b=4$ black balls. We sample $n=5$ without replacement. The number $X$ of white balls in the sample is Hypergeometric; here we observe $X=3$.
As with the Binomial distribution, we can obtain the PMF of the Hypergeometric distribution from the story.
Theorem 3.4.2 (Hypergeometric PMF). If $X \sim$ HGeom $(w, b, n)$, then the PMF of $X$ is
$$
P(X=k)=\frac{\left(\begin{array}{c}
w \
k
\end{array}\right)\left(\begin{array}{c}
b \
n-k
\end{array}\right)}{\left(\begin{array}{c}
w+b \
n
\end{array}\right)}
$$
for integers $k$ satisfying $0 \leq k \leq w$ and $0 \leq n-k \leq b$, and $P(X=k)=0$ otherwise.
Proof. To get $P(X=k)$, we first count the number of possible ways to draw exactly $k$ white balls and $n-k$ black balls from the urn (without distinguishing between different orderings for getting the same set of balls). If $k>w$ or $n-k>b$, then the draw is impossible. Otherwise, there are $\left(\begin{array}{c}w \ k\end{array}\right)\left(\begin{array}{c}b \ n-k\end{array}\right)$ ways to draw $k$ white and $n-k$ black balls by the multiplication rule, and there are $\left(\begin{array}{c}w+b \ n\end{array}\right)$ total ways to draw $n$ balls. Since all samples are equally likely, the naive definition of probability gives
$$
P(X=k)=\frac{\left(\begin{array}{c}
w \
k
\end{array}\right)\left(\begin{array}{c}
b \
n-k
\end{array}\right)}{\left(\begin{array}{c}
w+b \
n
\end{array}\right)}
$$
for integers $k$ satisfying $0 \leq k \leq w$ and $0 \leq n-k \leq b$. This PMF is valid because the numerator, summed over all $k$, equals $\left(\begin{array}{c}w+b \ n\end{array}\right)$ by Vandermonde’s identity (Example 1.5.3), so the PMF sums to 1 .
The Hypergeometric distribution comes up in many scenarios which, on the surface, have little in common with white and black balls in an urn. The essential structure of the Hypergeometric story is that items in a population are classified using two sets of tags: in the urn story, each ball is either white or black (this is the first set of tags), and each ball is either sampled or not sampled (this is the second set of tags). Furthermore, at least one of these sets of tags is assigned completely at random (in the urn story, the balls are sampled randomly, with all sets of the correct size equally likely). Then $X \sim \operatorname{HGeom}(w, b, n)$ represents the number items: in the urn story, balls that are both white and sampled.
统计代考
3.4 超几何
如果我们有一个装有 $w$ 白球和 $b$ 黑球的瓮,然后用替换从瓮中抽出 $n$ 个球会产生 $\operatorname{Bin}(n, w /(w+b))$在 $n$ 次试验中获得的白球数量的分布,因为抽签是独立的伯努利试验,每个试验的成功概率为 $w /(w+b)$。如果我们改为不放回抽样,如图 3.7 所示,那么白球的数量遵循超几何分布。
故事 3.4.1(超几何分布)。考虑一个装有 $w$ 白球和 $b$ 黑球的瓮。我们从瓮中随机抽出 $n$ 个球,没有放回,这样所有的 $\left(\begin{array}{c}w+b \ n\end{array}\right)$ 样本的可能性相同。令 $X$ 为样本中白球的数量。则称$X$ 具有参数$w、b$ 和$n$ 的超几何分布;我们用 $X \sim \operatorname{HGeom}(w, b, n)$ 来表示它。
116
图 $3.7$
超几何故事。一个瓮包含 $w=6$ 个白球和 $b=4$ 个黑球。我们对 $n=5$ 进行抽样而不进行替换。样本中白球的数量 $X$ 是超几何的;这里我们观察到 $X=3$。
与二项分布一样,我们可以从故事中获得超几何分布的 PMF。
定理 3.4.2(超几何 PMF)。如果 $X \sim$ HGeom $(w, b, n)$,则 $X$ 的 PMF 为
$$
P(X=k)=\frac{\left(\begin{数组}{c}
w \
ķ
\end{array}\right)\left(\begin{array}{c}
乙\
n-k
\end{array}\right)}{\left(\begin{array}{c}
w+b \
n
\end{数组}\right)}
$$
对于满足 $0 \leq k \leq w$ 和 $0 \leq n-k \leq b$ 的整数 $k$,否则 $P(X=k)=0$。
证明。为了得到$P(X=k)$,我们首先计算从瓮中准确地画出$k$白球和$nk$黑球的可能方法的数量(不区分获得同一组球的不同顺序) .如果 $k>w$ 或 $n-k>b$,那么平局是不可能的。否则,有 $\left(\begin{array}{c}w \ k\end{array}\right)\left(\begin{array}{c}b \ nk\end{array}\right )$ 用乘法规则绘制 $k$ 白球和 $nk$ 黑球的方法,有 $\left(\begin{array}{c}w+b \ n\end{array}\right)$绘制 $n$ 球的总方法。由于所有样本的可能性均等,因此概率的朴素定义给出
$$
P(X=k)=\frac{\left(\begin{数组}{c}
w \
ķ
\end{array}\right)\left(\begin{array}{c}
乙\
n-k
\end{array}\right)}{\left(\begin{array}{c}
w+b \
n
\end{数组}\right)}
$$
对于满足 $0 \leq k \leq w$ 和 $0 \leq n-k \leq b$ 的整数 $k$。这个 PMF 是有效的,因为对所有 $k$ 求和的分子等于 Vandermonde 恒等式 $\left(\begin{array}{c}w+b \ n\end{array}\right)$(示例 1.5. 3),所以 PMF 总和为 1 。
超几何分布出现在许多场景中,从表面上看,这些场景与瓮中的白球和黑球几乎没有共同之处。超几何故事的基本结构是人口中的项目使用两组标签进行分类:在骨灰盒故事中,每个球要么是白色的,要么是黑色的(这是第一组标签),每个球要么是抽样的,要么是未采样(这是第二组标签)。此外,这些标签组中的至少一组是完全随机分配的(在骨灰盒故事中,球是随机抽样的,所有组大小正确的可能性相同)。那么 $X \sim \operatorname{HGeom}(w, b, n)$ 代表数字项目:在骨灰盒故事中,球既是白色的又是采样的。
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。