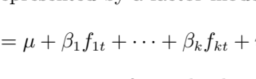物理代考| Density of Final States 量子力学代写
物理代写
5.3 Density of Final States
Suppose we are doing a scattering experiment in our simple model. We can prepare the target in a given state with energy $E_{n_{2}^{0}}$, and we can prepare an incident beam with a well-defined energy $E_{n_{1}^{0}}=\hbar^{2} k_{0}^{2} / 2 m_{1}$, where $k_{0}=$ $2 \pi n_{1}^{0} / L_{1}$. We certainly can achieve the energy resolution to determine that the target ends up in another state with discrete energy $E_{n_{2}}$; however, with the scattered particle, the situation is more complicated. Let us, for simplicity, call the size of the big region in which the first particle moves $L_{1} \equiv L$. The final particle energy is $E_{n_{1}}=\hbar^{2} k^{2} / 2 m_{1}$ with $k=2 \pi n_{1} / L$, and as $L$ becomes very large, these energies are very closely spaced. Thus no matter how small our resolution $d k$ is on the final particle, many final states will lie within this resolution! For large $L$, the number of these states $d n_{f}$ is
$$
d n_{f}=\frac{L}{2 \pi} d k \quad ; L \rightarrow \infty
$$
Thus all of these states will get into our final detector, and the transition rate that we actually measure is of necessity
$$
R_{f i} d n_{f}=R_{f i}\left(\frac{L}{2 \pi} d k\right) \quad ; \text { measured rate }
$$
Equation (5.28) then reads
$$
R_{f i} d n_{f}=\frac{2 \pi}{\hbar}\left|\left\langle n_{1}, n_{2}\left|H^{\prime}\right| n_{1}^{0}, n_{2}^{0}\right\rangle\right|^{2} \delta\left(E-E_{0}\right)\left(\frac{L}{2 \pi} d k\right)
$$
Multiply and divide this expression by $d E$. It is then possible to immediately do the integral over $E$ using Eq. (5.27), where we have summed over all of the energy-conserving events that get into our detector. Hence $^{4}$
$$
R_{f i} d n_{f}=\frac{2 \pi}{\hbar}\left|\left\langle n_{1}, n_{2}\left|H^{\prime}\right| n_{1}^{0}, n_{2}^{0}\right\rangle\right|^{2} \rho_{E}
$$
where $\rho_{E}$ is known as the density of final states
$$
\rho_{E}=\frac{L}{2 \pi}\left(\frac{d k}{d E}\right) \quad ; \text { density of final states }
$$
${ }^{4}$ We suppress the integral symbol on the l.h.s., although we have now used $\int \delta(E-$ $\left.E_{0}\right) d E=1$; we leave it this way because there are usually some variables left in $d n_{f}$ [see, for example, Eq. (5.43)].
40
Introduction to Quantum Mechanics
It follows that with a projectile energy of $E=\hbar^{2} k^{2} / 2 m_{1}$, this density of final states is given by
$$
\rho_{E}=\frac{L}{2 \pi}\left(\frac{m_{1}}{\hbar^{2} k}\right) \quad ; E=\frac{(\hbar k)^{2}}{2 m_{1}}
$$
物理代考
5.3 最终状态的密度
假设我们正在我们的简单模型中进行散射实验。我们可以用能量 $E_{n_{2}^{0}}$ 准备给定状态的目标,我们可以准备一个具有明确能量 $E_{n_{1}^{0}} 的入射光束=\hbar^{2} k_{0}^{2} / 2 m_{1}$,其中 $k_{0}=$ $2 \pi n_{1}^{0} / L_{1}$。我们当然可以实现能量分辨率,以确定目标最终处于另一个具有离散能量 $E_{n_{2}}$ 的状态;然而,有了散射粒子,情况就更加复杂了。为简单起见,我们将第一个粒子在其中移动的大区域的大小称为 $L_{1} \equiv L$。最终粒子能量为 $E_{n_{1}}=\hbar^{2} k^{2} / 2 m_{1}$ 其中 $k=2 \pi n_{1} / L$ 和 $ L$ 变得非常大,这些能量之间的间隔非常紧密。因此,无论我们在最终粒子上的分辨率 $d k$ 有多小,许多最终状态都将位于该分辨率内!对于较大的 $L$,这些状态 $d n_{f}$ 的数量为
$$
d n_{f}=\frac{L}{2 \pi} d k \quad ; L \rightarrow \infty
$$
因此所有这些状态都会进入我们的最终检测器,我们实际测量的转换率是必要的
$$
R_{f i} d n_{f}=R_{f i}\left(\frac{L}{2 \pi} d k\right) \quad ; \text { 测量速率 }
$$
等式(5.28)然后读取
$$
R_{f i} d n_{f}=\frac{2 \pi}{\hbar}\left|\left\langle n_{1}, n_{2}\left|H^{\prime}\right| n_{1}^{0}, n_{2}^{0}\right\rangle\right|^{2} \delta\left(E-E_{0}\right)\left(\frac{L} {2 \pi} dk\right)
$$
将此表达式乘以 $d E$。然后可以立即使用 Eq 对 $E$ 进行积分。 (5.27),我们总结了进入我们探测器的所有能量守恒事件。因此 $^{4}$
$$
R_{f i} d n_{f}=\frac{2 \pi}{\hbar}\left|\left\langle n_{1}, n_{2}\left|H^{\prime}\right| n_{1}^{0}, n_{2}^{0}\right\rangle\right|^{2} \rho_{E}
$$
其中 $\rho_{E}$ 被称为最终状态的密度
$$
\rho_{E}=\frac{L}{2 \pi}\left(\frac{d k}{d E}\right) \quad ; \text { 最终状态的密度 }
$$
${ }^{4}$ 尽管我们现在使用了 $\int \delta(E-$ $\left.E_{0}\right) d E=1$; 我们在 l.h.s. 上抑制了积分符号;我们这样保留它是因为 $d n_{f}$ 中通常会留下一些变量 [参见,例如,等式。 (5.43)]。
40
量子力学导论
因此,在 $E=\hbar^{2} k^{2} / 2 m_{1}$ 的抛射体能量下,这个终态密度由下式给出
$$
\rho_{E}=\frac{L}{2 \pi}\left(\frac{m_{1}}{\hbar^{2} k}\right) \quad ; E=\frac{(\hbar k)^{2}}{2 m_{1}}
$$
。

物理代考| Classical Optics量子力学代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程