物理代写| Gravitational Redshift Pound-Rebka Experiment 相对论代考代写 - 代考代写：100%准时可靠您的作业代写专家

0 0

By admin Physics代写数学代写物理物理代写相对论代写 2022年3月1日

代写隐藏

1 物理代写| Gravitational Redshift Pound-Rebka Experiment 相对论代考

物理代写| Gravitational Redshift Pound-Rebka Experiment 相对论代考

物理代写

7.4 Gravitational Redshift: Pound-Rebka Experiment
127
7.4 Gravitational Redshift: Pound-Rebka Experiment
Gravitational redshift is a fundamental prediction of GR, which not only provides an important validation of the theory, but is crucial in day-to-day life, specifically in Global Positioning System (GPS) primarily used for navigation. This topic has been covered in the previous chapters and the expressions were derived for Schrawzschild geometry in Chapter 6 . Here we describe the first gravitational redshift measurement due to earth’s gravitational field.

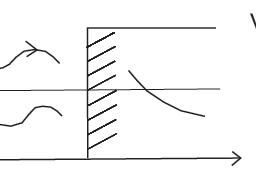
In 1959 Robert Pound and Glenn Rebka devised an experiment at Harvard University to test the gravitational redshift prediction of General Relativity. They placed atomic gamma ray emitters on top of a tower and the same material at the bottom of the tower which would absorb those photons. However, due to gravitational blue shift, the frequency of the emitted photons increases when they reach the bottom of the tower, which does not match the difference in energy levels required for the atoms are given the right amount of upward velocity (that is, away from the receiver atoms) that could compensate for the gravitational blueshift and then the photons would get absorbed. This is the basic principle for the experiment.

If $R$ is the radius of the earth, the $h(h \ll R)$ height of the tower, $\lambda_{e}$ the wavelength of the emitted photons and $\lambda_{r}$ the wavelength when the photons reach the receiver atoms, then from the gravitational redshift formula, Eq. (6.5.3), we obtain:
$\frac{\lambda_{r}}{\lambda_{e}}=\left[\frac{\left(g_{00}\right){r}}{\left(g{00}\right){e}}\right]^{1 / 2}=\frac{\left(1-\frac{2 m}{R}\right)^{1 / 2}}{\left(1-\frac{2 m}{R+h}\right)^{1 / 2}} \approx 1+\frac{m}{R+h}-\frac{m}{R} \approx 1-\frac{m h}{R^{2}}$ where, as usual $m=G M{\oplus} / c^{2}$, and $M_{\oplus}$ is the mass of the earth. If the emitter atoms are given a velocity $v$ upwards and if $\lambda_{0}$ is the wavelength of the photons in the rest frame of the atoms, due to special relativistic Doppler shift the effective emitted wavelength $\lambda_{e}$ becomes,
$$
\lambda_{e}=\sqrt{\frac{1+v / c}{1-v / c}} \lambda_{0} \approx(1+v / c) \lambda_{0}
$$
Thus the wavelength of the photons received at the bottom of the tower is,
$$
\lambda_{r}=\left(1-\frac{m h}{R^{2}}\right)\left(1+\frac{v}{c}\right) \lambda_{0} .
$$
In order for the received photons to have the same wavelength, $\lambda_{r}=\lambda_{0}$, so that they could be absorbed by the receiving atoms in their rest frame, requires, to the first order, $v / c=m h / R^{2}=G M_{\oplus} h /(R c)^{2}=g h / c^{2}$, where $g$ is the acceleration due to gravity at the surface of the earth.
128
7 Classical Tests of General Relativity
In the set up used by Pound and Rebka, the emitters were kept at a height of $h=22.5 \mathrm{~m}$ with respect to the receiving atoms. Hence, the velocity required for the emitters to satisfy the absorption criteria described above, $v \approx 2.5 \times 10^{-15} \mathrm{c}=$ $7.5 \times 10^{-7} \mathrm{~m} / \mathrm{s}$. However, this velocity is much smaller (by five orders of magnitude) than the recoil velocity of each atom when it emits or absorbs a photon. To alleviate this problem, Pound and Rebka made use of Mössbauer spectroscopy, where the that, as a whole, reacted to the recoil momentum, significantly reducing the recoil velocity. In the experiment, the emitter was mounted on a loudspeaker cone which moved the emitting atoms with sinusoidally varying velocity. When the velocity matched the required value to compensate for the gravitational redshift, the photons would get absorbed by the receiving atoms. This showed a variation in the reading of a scintillation counter kept below the receiver. To rule out spurious correlations, the experiment was performed for different loudspeakers for a range of oscillation frequencies. The results matched the prediction and GR successfully passed yet another test.

物理代考

7.4 引力红移：Pound-Rebka 实验
127
7.4 引力红移：Pound-Rebka 实验
引力红移是对 GR 的基本预测，它不仅提供了对理论的重要验证，而且在日常生活中至关重要，特别是在主要用于导航的全球定位系统 (GPS) 中。这个主题已经在前面的章节中讨论过，并且表达式是在第 6 章中为 Schrawzschild 几何推导的。在这里，我们描述了由于地球引力场引起的第一次引力红移测量。

1959 年，罗伯特·庞德和格伦·雷布卡在哈佛大学设计了一个实验来测试广义相对论的引力红移预测。他们在塔顶放置了原子伽马射线发射器，在塔底放置了相同的材料来吸收这些光子。然而，由于引力蓝移，发射光子的频率在到达塔底时会增加，这与给定适当的向上速度（即远离来自接收器原子）可以补偿引力蓝移，然后光子会被吸收。这是实验的基本原理。

如果$R$是地球的半径，$h(h \ll R)$是塔的高度，$\lambda_{e}$是发射光子的波长，$\lambda_{r}$是当光子到达接收器原子，然后从引力红移公式，方程。 (6.5.3)，我们得到：
$\frac{\lambda_{r}}{\lambda_{e}}=\left[\frac{\left(g_{00}\right){r}}{\left(g{00}\right) {e}}\right]^{1 / 2}=\frac{\left(1-\frac{2 m}{R}\right)^{1 / 2}}{\left(1-\frac {2 m}{R+h}\right)^{1 / 2}} \约 1+\frac{m}{R+h}-\frac{m}{R} \约 1-\frac{mh }{R^{2}}$ 其中，与往常一样，$m=G M{\oplus} / c^{2}$，$M_{\oplus}$ 是地球的质量。如果给定发射器原子向上的速度 $v$ 并且如果 $\lambda_{0}$ 是原子静止框架中光子的波长，由于特殊的相对论多普勒频移，有效发射波长 $\lambda_{e }$ 变成，
$$
\lambda_{e}=\sqrt{\frac{1+v / c}{1-v / c}} \lambda_{0} \approx(1+v / c) \lambda_{0}
$$
因此，在塔底接收到的光子的波长是，
$$
\lambda_{r}=\left(1-\frac{m h}{R^{2}}\right)\left(1+\frac{v}{c}\right) \lambda_{0} 。
$$
为了使接收到的光子具有相同的波长，$\lambda_{r}=\lambda_{0}$，以便它们可以被静止框架中的接收原子吸收，一阶需要 $v / c=mh / R^{2}=G M_{\oplus} h /(R c)^{2}=gh / c^{2}$，其中$g$为地表重力加速度地球的。
128
广义相对论的 7 个经典检验
在 Pound 和 Rebka 使用的设置中，发射器相对于接收原子保持在 $h=22.5 \mathrm{~m}$ 的高度。因此，发射器满足上述吸收标准所需的速度， $v \approx 2.5 \times 10^{-15} \mathrm{c}=$ $7.5 \times 10^{-7} \mathrm{~m } / \mathrm{s}$。然而，这个速度比每个原子发射或吸收光子时的反冲速度要小得多（五个数量级）。为了缓解这个问题，Pound 和 Rebka 使用了穆斯堡尔光谱，作为一个整体，它对反冲动量做出反应，显着降低了反冲速度。在实验中，发射器安装在扬声器锥体上，以正弦变化的速度移动发射原子。当速度与补偿引力红移所需的值相匹配时，光子将被接收原子吸收。这显示了在接收器下方的闪烁计数器读数的变化。为了排除虚假相关性，针对不同的扬声器针对一系列振荡频率进行了实验。结果与预测相符，GR 成功通过了另一项测试。