物理代写| Special Relativity 狭义相对论代考代写 - 代考代写：100%准时可靠您的作业代写专家

The theory of Special Relativity (SR) was introduced by A. Einstein in 1905. It deals with the observations of inertial observers in the absence of gravity. The theory of General Relativity (GR) that includes gravitation, and thus acceleration, was published in 1915. For English translations, see Einstein (1905). The latter theory predicted the deflection of light near a massive body, like the sun. Shortly after the end of the first world war, a British team, led by A. S. Eddington, confirmed this startling prediction. This made Einstein world famous, even among people who had no particular interest in science.

In relativity, an observation is the assignment of coordinates $x^{\mu}, \mu=$ $0,1,2,3$, for the time and space location of an event. Space is continuous, and functions of the coordinates can be differentiated. Upon partial differentiation with respect to one of the coordinates, the others are held constant. This insures that the coordinates are independent,
$$
x^{\mu},{\nu} \equiv \frac{\partial x^{\mu}}{\partial x^{\nu}}=\delta^{\mu}{ }{\nu}=\delta_{\nu}^{\mu}=1, \quad \mu=\nu, \quad \delta^{\mu}{ }{\nu}=0, \quad \mu \neq \nu $$ As will be seen $\delta{\nu}^{\mu}$ is the Kronecker delta tensor. The superscript, subscript indexes are termed contravariant, covariant. Note the shorthand notation for the partial derivative, by use of a comma. Such a shorthand will keep some of the formulas of GR, with many partial derivatives, to a reasonable length.

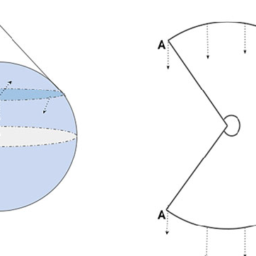
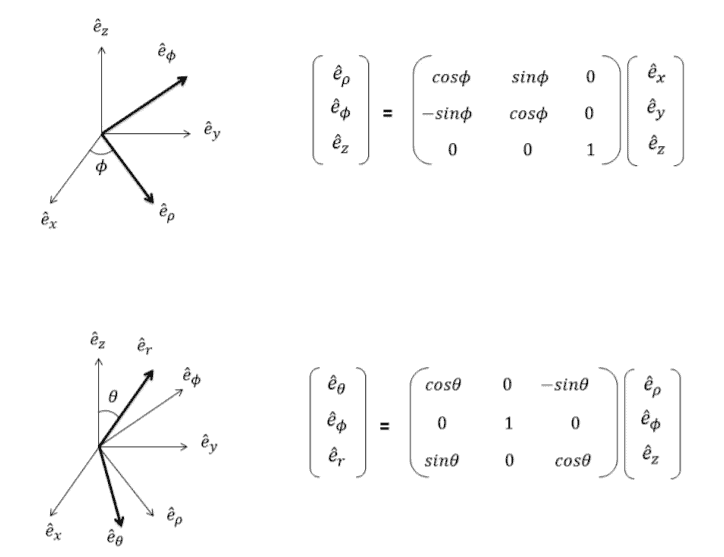
In rectangular coordinates $x^{\mu}=(t, x, y, z)$. In relativity, one may transform to other coordinate systems, or to the rectangular coordinates of other reference frames. These coordinates will be labeled by primes, $x^{\mu^{\prime}}$. Curvilinear coordinates are particularly useful, and a rotation carries you from one set of coordinates to the other. In cylindrical coordinates $x^{\mu^{\prime}}=(t, \rho, \phi, z)$ because as illustrated in Fig. 1.1, the rotation changes the direction indicating unit vectors $\left(\hat{e}{x}, \hat{e}{y}\right) \rightarrow\left(\hat{e}{\rho}, \hat{e}{\phi}\right)$. Similarly, for spherical coordinates $x^{\mu^{\prime \prime}}=(t, \theta, \phi, r),\left(\hat{e}{\rho}, \hat{e}{z}\right) \rightarrow\left(\hat{e}{\theta}, \hat{e}{r}\right) .$ Other texts employ an extra renaming, and take $x^{\mu^{\prime \prime}}=0-3=t, r, \theta, \phi$, but a rose by any name would smell sweet. The reader can prove that the components of 3 -vectors, when written in terms of unit vectors $\vec{V}=V^{x} \hat{e}{x}+V^{y} \hat{e}{y}+V^{z} \hat{e}_{z}$, are transformed by rotations in the same way as the unit vectors.

Lorentz Transform

Two observers $\mathrm{O}$ and $\mathrm{O}^{\prime}$ are considered. They use parallel axes and rectangular coordinates. Rotations, like those in Fig. 1.1, allow them to align their $z$-axes along the relative velocity. $\mathrm{O}$ uses $x^{\mu}$, and says $\mathrm{O}^{\prime}$ is moving in the $z$-direction with speed $V(<1)$, while $\mathrm{O}^{\prime}$ uses $x^{\mu^{\prime}}$, and says $\mathrm{O}$ is moving in the $-z$-direction with speed $V$.

When their origins overlapped, the clocks were synchronized $t=x^{0}=$ $t^{\prime}=x^{0^{\prime}}=0 .$ In this geometry, $(x, y)=\left(x^{\prime}, y^{\prime}\right)$ or $x^{1,2}=x^{1^{\prime}, 2^{\prime}}$, as there is no relative motion in these directions. However, $c=1$ for both observers, so space and time are interconnected, and now termed spacetime. If $\mathrm{O}^{\prime}$ says that events led to changes in coordinates $d z^{\prime}=d x^{3^{\prime}}$ and $d t^{\prime}=d x^{0^{\prime}}$, the components of the displacement vector $d r^{\mu^{\prime}}$, then $\mathrm{O}$ would calculate from the chain rule of differential calculus,
$$ d x^{3}=d z=\frac{\partial z}{\partial z^{\prime}} d z^{\prime}+\frac{\partial z}{\partial t^{\prime}} d t^{\prime}+\frac{\partial z}{\partial x^{\prime}} d x^{\prime}+\frac{\partial z}{\partial y^{\prime}} d y^{\prime} \equiv x^{3}, \mu^{\prime} d x^{\mu^{\prime}} $$ $=x^{3}, 3^{\prime} d x^{3^{\prime}}+x^{3}, 0^{\prime} d x^{0^{\prime}}$, $$ d x^{0}=d t=\frac{\partial t}{\partial z^{\prime}} d z^{\prime}+\frac{\partial t}{\partial t^{\prime}} d t^{\prime}+\frac{\partial t}{\partial x^{\prime}} d x^{\prime}+\frac{\partial t}{\partial y^{\prime}} d y^{\prime} \equiv x^{0},_{\mu^{\prime}} d x^{\mu^{\prime}} $$ $=x^{0}, 3^{\prime} d x^{3^{\prime}}+x^{0}, 0^{\prime} d x^{0^{\prime}} .$ One notes that, similar to rotations, this transform can be represented by matrix multiplication, $$ \left(\begin{array}{l}d x^{0} \ d x^{1} \ d x^{2} \ d x^{3}\end{array}\right)=\left(\begin{array}{cccc}x^{0}, 0^{\prime} & 0 & 0 & x^{0}, 3^{\prime} \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ x^{3}, 0^{\prime} & 0 & 0 & x^{3}, 3^{\prime}\end{array}\right)\left(\begin{array}{l}d x^{0^{\prime}} \ d x^{1^{\prime}} \ d x^{2^{\prime}} \ d x^{3^{\prime}}\end{array}\right) $$ matrix multiplication,

This is a linear transform. The vector components appear to the power unity. The coefficients, the partial derivatives multiplying the $\mathrm{O}^{\prime}$ vector components, are relations between the coordinates of the different frames. They are independent of the vectors. Such a rule for vector transformation is not limited to rotations. It works for any coordinate transformation, and any vector. If each vector had a different transformation rule, there would be no theory. If a set of four quantities $V^{\mu}$ do not transform as above, then they are not components of a vector.

Spacetime Diagrams

Many GR texts stress the concept of spacetime diagrams. Analytic calculations are favored by this author. However, for completeness, the former are briefly discussed in this section. One draws on a flat sheet, and must be concerned with four coordinates. Thus, one-dimensional motion, in the $z$-direction, is considered.

物理代考

在直角坐标中$x^{\mu}=(t, x, y, z)$。在相对论中，人们可以转换到其他坐标系，或者转换到其他参考系的直角坐标。这些坐标将用素数标记，$x^{\mu^{\prime}}$。曲线坐标特别有用，旋转将您从一组坐标带到另一组坐标。在柱坐标 $x^{\mu^{\prime}}=(t, \rho, \phi, z)$ 因为如图 1.1 所示，旋转改变了指示单位向量 $\left(\hat 的方向{e}{x}, \hat{e}{y}\right) \rightarrow\left(\hat{e}{\rho}, \hat{e}{\phi}\right)$。类似地，对于球坐标 $x^{\mu^{\prime \prime}}=(t, \theta, \phi, r),\left(\hat{e}{\rho}, \hat{e} {z}\right) \rightarrow\left(\hat{e}{\theta}, \hat{e}{r}\right) .$ 其他文本采用额外的重命名，并取 $x^{\mu^ {\prime \prime}}=0-3=t, r, \theta, \phi$，但是任何名字的玫瑰都会闻起来很香。读者可以证明 3 向量的分量，当写成单位向量 $\vec{V}=V^{x} \hat{e}{x}+V^{y} \hat{e} {y}+V^{z} \hat{e}_{z}$, 以与单位向量相同的方式通过旋转进行变换。

正如将要看到的，我们生活在四个维度的时空中，时空相互混合。因此，时空向量有四个分量。以三空间类推，将坐标$x^{\mu}$作为逆变位置向量$r^{\mu}$的矩形分量。那么$d x^{\mu}$ 也一定是位移向量$d r^{\mu}$ 的分量，因为两个向量的差也是一个向量。到目前为止，这些是我们已知的唯一向量。在后面的章节中，当重力或加速度起作用时，一组坐标的符号可能有一个条形$x^{\bar{\mu}}$。这将表明这些坐标是使用直角坐标的惯性观察者的坐标。这是任意大的 SR 参考帧的情况。当重力存在时，条通常会不存在。然而，正如将要展示的那样，即使存在重力，在空间中的任何一点都可以找到一个局部惯性系。该框架可能需要任意小。当描述坐标集时，该框架的直角坐标将具有条形。其他惯性参考系的其他坐标系或直角坐标将由条形和一个或多个素数$x^{\bar{\mu}^{\prime}}$表示。在这种情况下，向量 $r^{\bar{\mu}}$ 和更高阶张量 $T^{\bar{\mu} \bar{\nu}}$ 的分量也将具有条形。爱因斯坦从两个假设中发展了 SR：（1）所有惯性观察者的物理定律都是相同的，无论它们的相对速度如何； (2) 所有惯性观测者在真空中测量相同的光速 $c=3 \times$ $10^{8} \mathrm{~m} / \mathrm{s}$。第二个假设与牛顿关于时间独立于其他一切流动的概念发生冲突。这导致观察到，与一个观察者同时发生的事件对另一个观察者可能不是这样。 $c$ 也成为限制速度以保持因果关系。在GR中，“惯性”一词被删除，并且必须考虑等效原理：当自由落入具有均匀重力的区域时不会经历重力效应。

洛伦兹变换

考虑了两个观察者 $\mathrm{O}$ 和 $\mathrm{O}^{\prime}$。它们使用平行轴和直角坐标。旋转，如图 1.1 中的那些，允许它们沿相对速度对齐它们的 $z$ 轴。 $\mathrm{O}$ 使用 $x^{\mu}$，并表示 $\mathrm{O}^{\prime}$ 以 $V(<1)$ 的速度沿 $z$ 方向移动，而 $\mathrm{O}^{\prime}$ 使用 $x^{\mu^{\prime}}$，并表示 $\mathrm{O}$ 正以 $-z$ 方向以速度 $ 移动V$。

当它们的起源重叠时，时钟是同步的 $t=x^{0}=$ $t^{\prime}=x^{0^{\prime}}=0 .$ 在这个几何中，$(x, y )=\left(x^{\prime}, y^{\prime}\right)$ 或 $x^{1,2}=x^{1^{\prime}, 2^{\prime}}$ ，因为在这些方向上没有相对运动。然而，对于两个观察者来说，$c=1$，所以空间和时间是相互关联的，现在称为时空。如果 $\mathrm{O}^{\prime}$ 说事件导致坐标的变化 $dz^{\prime}=dx^{3^{\prime}}$ 和 $dt^{\prime}=dx ^{0^{\prime}}$，位移向量$dr^{\mu^{\prime}}$的分量，则$\mathrm{O}$会根据微积分的链式法则计算，
$$ dx^{3}=dz=\frac{\partial z}{\partial z^{\prime}} dz^{\prime}+\frac{\partial z}{\partial t^{\prime} } dt^{\prime}+\frac{\partial z}{\partial x^{\prime}} dx^{\prime}+\frac{\partial z}{\partial y^{\prime}} dy ^{\prime} \equiv x^{3}, \mu^{\prime} dx^{\mu^{\prime}} $$ $=x^{3}, 3^{\prime} dx^{ 3^{\prime}}+x^{3}, 0^{\prime} dx^{0^{\prime}}$, $$ dx^{0}=dt=\frac{\partial t}{ \partial z^{\prime}} dz^{\prime}+\frac{\partial t}{\partial t^{\prime}} dt^{\prime}+\frac{\partial t}{\partial x^{\prime}} dx^{\prime}+\frac{\partial t}{\partial y^{\prime}} dy^{\prime} \equiv x^{0},_{\mu^ {\prime}} dx^{\mu^{\prime}} $$ $=x^{0}, 3^{\prime} dx^{3^{\prime}}+x^{0}, 0 ^{\prime} dx^{0^{\prime}} .$ 有人注意到，类似于旋转，这种变换可以用矩阵乘法表示，$$ \left(\begin{array}{l}dx^{ 0} \ dx^{1} \ dx^{2} \ dx^{3}\end{array}\right)=\left(\begin{array}{cccc}x^{0}, 0 ^{\prime} & 0 & 0 & x^{0}, 3^{\prime} \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ x^{3}, 0^ {\prim e} & 0 & 0 & x^{3}, 3^{\prime}\end{array}\right)\left(\begin{array}{l}dx^{0^{\prime}} \ dx^{1^{\prime}} \dx^{2^{\prime}} \dx^{3^{\prime}}\end{array}\right) $$ 矩阵乘法，

这是一个线性变换。矢量分量似乎是幂单位。系数，即与 $\mathrm{O}^{\prime}$ 矢量分量相乘的偏导数，是不同帧坐标之间的关系。它们独立于向量。这种矢量变换的规则不限于旋转。它适用于任何坐标变换和任何矢量。如果每个向量都有不同的变换规则，就不会有理论。如果一组四个量 $V^{\mu}$ 没有像上面那样变换，那么它们不是向量的分量。