物理代写| Gravity and Curvature of Space-Time 相对论代考
物理代写
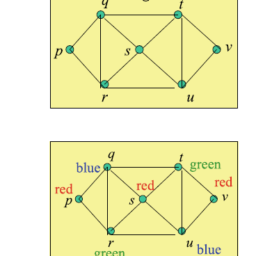
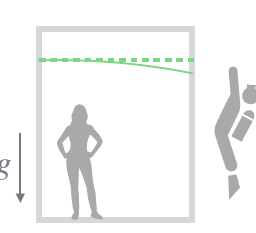
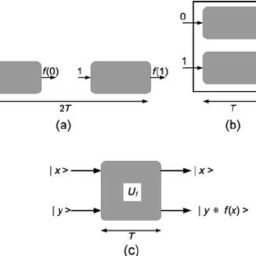
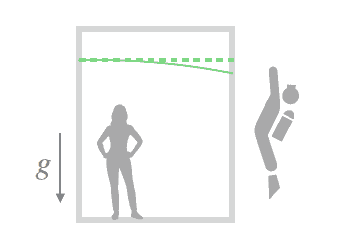
The strong equivalence principle creates apparent contradictions. Special relativity postulates that the velocity of light is constant and light travels in a straight line. Now imagine an observer shining a laser light in a freely falling elevator perpendicular to the motion of the elevator (of course, without knowing which way the elevator is moving). This observer should see the light ray travel in a straight line. However, if there is another observer who is stationary outside the elevator, and who experiences the gravitational field, say in the “downward” direction (here downwards is defined by the direction of the acceleration due to gravity), would see the ray bend downwards. This observer would therefore naturally conclude that light bends when in a gravitational field. This situation is depicted in Fig. 2.1. The dashed line which is straight, represents in the light ray in the local inertial frame of the falling elevator and the solid curve represents the light ray from the view point of the external stationary observer in a gravitational field.
Here we would like to mention that this is just half the story. Although the equivalence principle shows qualitatively that light must bend in a gravitational field it does not give the full answer. See Exercise 2.3.2. In fact, to delve into history, Einstein had used the equivalence principle to compute the bending of a light ray emitted
Fig. $2.1$ An illustration showing that a laser light ray must
Fig. $2.1$ An illustration showing that a laser light ray must bend for the outside stationary observer who experiences a gravitational field. On the other hand, for the observer falling with the elevator, since special relativity holds in an inertial frame for a freely falling observer, the light ray travels in a straight line
32
2 The Equivalence Principle
by a background star, just grazing the Sun’s surface and observed on Earth. This was in 1911 before he had given his field equations, which he gave in 1915 . The experiment to verify this prediction at that time could only be performed during a solar eclipse, when the background stars would be visible. But as it happened at that time the experiment could not be carried out because of world war I (fortunately for relativity and Einstein!). Because Einstein’s computation using only the equivalence principle led to half of the observed value measured later! The reason for this discrepancy is because equivalence principle is one of the causes effecting the bending of light; there is another cause, namely, the curvature. This curvature results from the Einstein’s field equations which were given in 1915 . The full computation is given in Sect. 7.2.Z
物理代考
2.3 时空的引力和曲率
我们现在要求 SR 在每个 LIF 中都有效。但请注意,LIF 只是本地的。问题是如何在局部性不成立的大范围内描述物理学。这当然可以通过将 LIF 拼接在一起来实现。例如,对于像地球这样的球对称物体,必须将自由下落的 LIF 拼接在一起,这些 LIF 都是径向下落的。这自然会导致一个弯曲空间的概念,或者因为空间和时间在 SR 中已经结合在一起,所以弯曲时空的概念。
高斯和黎曼已经研究过弯曲空间。球体是一个非常简单的弯曲空间。它可以被认为是以正确的方式将小的扁平件放在一起。任何光滑的表面都是如此——它可以由小的扁平件构成。这个想法非常适合上述情况。自由下落的框架或 LIF 是 SR 在其中有效的扁平部分,而将它们组合在一起将产生较大的物理效果。这自然导致了用弯曲时空来描述 GR 或引力的想法。为了做到这一点,我们将需要许多处理弯曲空间所需的工具,这些工具通常被称为可微流形。像球体这样的表面是二维弯曲空间或可微流形二维,因为只需要两个坐标,比如 $\theta, \phi$ 来局部描述空间。它是弯曲的,因为欧几里得的几何在其中无效。例如,如果一个人在一个球体上构造一个三角形,现在每一边都由大圆弧组成(这些是人们可以在球体表面上绘制的最直的可能曲线,因此可以代替直线),则三角形内角之和不等于 $180^{\circ} .$ 但在欧几里得几何中,三角形内角之和必须等于 $180^{\circ}$。这个论证表明球体不是欧几里得空间。这就是所谓的弯曲空间。球体是二维的弯曲空间——我们稍后会定义曲率。平面的曲率为零或称为平坦,而球体的曲率不为零且称为弯曲。然而,在 SR 和 GR 中,我们需要 3 个空间坐标和 1 个时间坐标来描述时空,因此我们处理的是 4 维时空。
$2.3$ 时空的引力和曲率
31
在 SR 中,时空是平坦的,表明没有重力,而在有重力的 GR 中,时空是弯曲的。此外,我们将需要张量和张量演算来描述物理——物理场。由于引力物理学必然涉及弯曲空间,因此必须处理一般坐标变换——不仅仅是惯性系之间的洛伦兹变换——因此我们将要处理的张量必须在这些一般坐标变换下变换。这将在后面的章节中讨论。现在让我们看看仅使用等价原理和自由落体框架可以得出什么结果。
强对等原则造成了明显的矛盾。狭义相对论假设光速是恒定的,并且光沿直线传播。现在想象一个观察者在垂直于电梯运动的自由下落的电梯中照射激光(当然,不知道电梯的运动方向)。这个观察者应该看到光线以直线传播。但是,如果有另一个观察者在电梯外静止,并且经历了引力场,比如在“向下”方向(这里向下由重力加速度的方向定义),会看到光线向下弯曲.因此,这位观察者自然会得出结论,光线在引力场中会发生弯曲。这种情况如图 2.1 所示。直线的虚线代表下落电梯的局部惯性系中的光线,实线代表引力场中外部静止观察者视点的光线。
在这里,我们想提一下,这只是故事的一半。尽管等效原理定性地表明光必须在引力场中弯曲,但它并没有给出完整的答案。见练习 2.3.2。事实上,为了深入研究历史,爱因斯坦使用等效原理来计算发出的光线的弯曲
Fig. $2.1$ 说明激光束必须
Fig. $2.1$ 一个说明激光束必须弯曲的外部静止观察者体验引力场。另一方面,对于随电梯下落的观察者,由于狭义相对论对于自由下落的观察者来说成立于惯性系中,所以光线沿直线传播
32
2 等价原则
由一颗背景恒星,刚刚掠过太阳表面并在地球上观察到。这

物理代考Gravity and Curvature of Space-Time 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
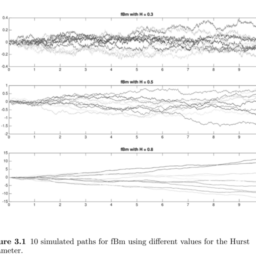
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程