数学代写代考| Graph Colouring and Four-Colour Problem 离散数学代写 - 代考代写：100%准时可靠您的作业代写专家

It is very common for maps to be coloured in such a way that neighbouring states or countries are coloured differently. This allows different states or countries to be easily distinguished as well as the borders between them. The question naturally arises as to how many colours are needed (or determining the least number of colours needed) to colour the entire map, as it might be expected that a large number of colours would be needed to colour a large complicated map.

However, it may come as a surprise that in fact very few colours are required to colour any map. A former student of the British logician, Augustus De Morgan, had noticed this in the mid-1800s, and he proposed the conjecture of the four-colour theorem. There were various attempts to prove that 4 colours were sufficient from the mid-1800s onwards, and it remained a famous unsolved problem in mathematics until the late twentieth century.

Kempe gave an erroneous proof of the four-colour problem in 1879 , but his attempt led to the proof that five colours are sufficient (which was proved by Heawod in the late 1800 s). Appel and Haken of the University of Illinois finally provided the proof that 4 colours are sufficient in the mid-1970s (using over $1000 \mathrm{~h}$ of computer time in their proof).

Each map in the plane can be represented by a graph, with each region of the graph represented by a vertex. Edges connect two vertices if the regions have a common border. The colouring of a graph is the assignment of a colour to each vertex of the graph so that no two adjacent vertices in this graph have the same colour.
Definition
Let $\mathrm{G}=(\mathrm{V}, \mathrm{E})$ be a graph and let $\mathrm{C}$ be a finite set called the colours. Then, a colouring of $\mathrm{G}$ is a mapping $\kappa: \mathrm{V} \rightarrow \mathrm{C}$ such that if $u v \in \mathrm{E}$ then $\kappa(u) \neq \kappa(v)$.
That is, the colouring of a simple graph is the assignment of a colour to each vertex of the graph such that if two vertices are adjacent then they are assigned a different colour. The chromatic number of a graph is the least number of colours needed for a colouring of the graph. It is denoted by $\chi(G)$.

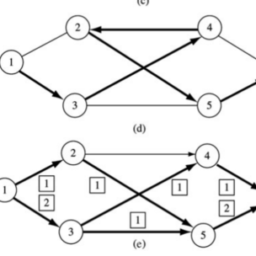
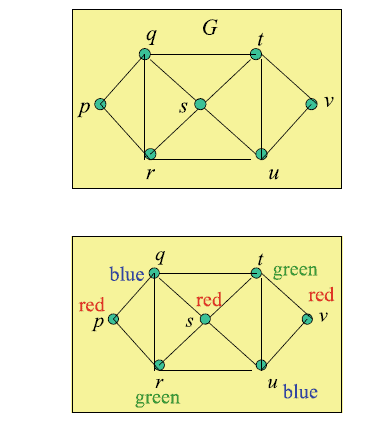
Example 9.2 Show that the chromatic colour of the following graph $G($ Fig. $9.9)$ is 3 (this example is adapted from [2]).
Solution
The chromatic colour of $\mathrm{G}$ must be at least 3 since vertices $p, q$ and $r$ must have different colours, and so we need to show that 3 colours are in fact sufficient to colour G. We assign the colours red, blue and green to $p, q$ and $r$ respectively. We immediately deduce that the colour of $s$ must be red (as adjacent to $q$ and $r$ ). From this, we deduce that $t$ is coloured green (as adjacent to $q$ and $s$ ) and $u$ is coloured blue (as adjacent to $s$ and $t$ ). Finally, $v$ must be coloured red (as adjacent to $u$ and $t$ ). This leads to the colouring of the graph $\mathrm{G}$ in Fig. 9.10.

Theorem $9.8$ (Four-Colour Theorem) The chromatic number of a planar graph $G$ is less than or equal to 4 .

地图以这样的方式着色是很常见的，即邻国或国家的颜色不同。这样可以轻松区分不同的州或国家以及它们之间的边界。自然会出现一个问题，即需要多少颜色（或确定所需的最少颜色数量）来为整个地图着色，因为可能预期需要大量颜色来为大型复杂地图着色。

然而，令人惊讶的是，实际上任何地图都需要很少的颜色来着色。英国逻辑学家奥古斯都德摩根的前学生在 1800 年代中期注意到了这一点，他提出了四色定理的猜想。从 1800 年代中期开始，有各种尝试证明 4 种颜色就足够了，直到 20 世纪后期，它仍然是数学中一个著名的未解决问题。

Kempe 在 1879 年对四色问题给出了一个错误的证明，但他的尝试导致了五色足够的证明（Heawod 在 1800 年代后期证明了这一点）。伊利诺伊大学的 Appel 和 Haken 最终证明了 1970 年代中期 4 种颜色就足够了（在他们的证明中使用了超过 1000 美元的计算机时间）。

平面中的每张地图都可以用一个图来表示，图中的每个区域都用一个顶点表示。如果区域具有公共边界，则边连接两个顶点。图的着色是为图的每个顶点分配一种颜色，以使该图中没有两个相邻的顶点具有相同的颜色。
定义
令 $\mathrm{G}=(\mathrm{V}, \mathrm{E})$ 是一个图，而 $\mathrm{C}$ 是一个称为颜色的有限集。那么，$\mathrm{G}$ 的着色是一个映射 $\kappa: \mathrm{V} \rightarrow \mathrm{C}$ 使得如果 $uv \in \mathrm{E}$ 那么 $\kappa( u) \neq \kappa(v)$。
也就是说，简单图的着色是将颜色分配给图的每个顶点，这样如果两个顶点相邻，则为它们分配不同的颜色。图形的色数是图形着色所需的最少颜色数。记为$\chi(G)$。

例 9.2 证明下图 $G($ Fig. $9.9)$ 的彩色为 3（本例改编自[2]）。
解决方案
$\mathrm{G}$ 的颜色必须至少为 3，因为顶点 $p、q$ 和 $r$ 必须具有不同的颜色，因此我们需要证明 3 种颜色实际上足以为 G 着色。我们将红色、蓝色和绿色分别分配给 $p、q$ 和 $r$。我们立即推断出 $s$ 的颜色必须是红色（与 $q$ 和 $r$ 相邻）。由此，我们推断 $t$ 为绿色（与 $q$ 和 $s$ 相邻），$u$ 为蓝色（与 $s$ 和 $t$ 相邻）。最后，$v$ 必须为红色（与 $u$ 和 $t$ 相邻）。这导致图 $\mathrm{G}$ 在图 9.10 中着色。

定理 $9.8$ (四色定理) 平面图 $G$ 的色数小于等于 4 。

图论代考

自然数 $\mathbb{N}$ 由数字 $\{1,2,3, \ldots\}$ 组成。整数 $\mathbb{Z}$ 由 $\{\ldots-2,-1,0,1,2, \ldots\}$ 组成。有理数 $\mathbb{Q}$ 由 $\left\{{ }^{p} /_{q}\right.$ 形式的所有数字组成，其中 $p$ 和 $q$ 是整数，$ \left.q \neq 0\right\}$。实数 $\mathbb{R}$ 被定义为有理数收敛序列的集合，它们是有理数的超集。它们包含有理数和无理数。复数 $\mathbb{C}$ 由 $\{a+bi$ 形式的所有数字组成，其中 $a, b \in \mathbb{R}$ 和 $i=\sqrt{-} 1\}美元。毕达哥拉斯三元组（图 3.2）是满足毕达哥拉斯方程 $x^{2}+y^{2}=z^{2}$ 的三个整数的组合。有无数个这样的三元组，这种三元组的一个例子是 $3,4,5$，因为 $3^{2}+4^{2}=5^{2}$。毕达哥拉斯学派发现了音乐和数字之间的数学关系，他们的哲学是数字隐藏在从音乐到科学和自然的一切事物中。这导致了他们的哲学，即“一切都是数字”。

数学代写| DISCRETE MATHEMATICS代考请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

Cryptosystem
A system that describes how to encrypt or decrypt messages
Plaintext
Message in its original form
Ciphertext
Message in its encrypted form
Cryptographer
Invents encryption algorithms
Cryptanalyst
Breaks encryption algorithms or implementations

编码理论代写

编码理论（英语：Coding theory）是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错，最近也用于网络编码中。不同学科（如信息论、电机工程学、数学、语言学以及计算机科学）都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正（或检测）数据传输中的错误。

编码共分四类：^[1]