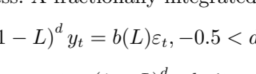数学代写|Summation by parts 数论代考
数论代考
Analytic number theory makes very frequent use of “summation by parts”, which is a discrete form of integration by parts. We state the version that we use.
LEMMA A.1.1 (Summation by parts). Let $\left(a_{n}\right){n \geqslant 1}$ be a sequence of complex number and $f:\left[0,+\infty\left[\rightarrow \mathrm{C}\right.\right.$ a function of class $\mathrm{C}^{1}$. For all $x \geqslant 0$, define $$ \mathrm{M}{a}(x)=\sum_{1 \leqslant n \leqslant x} a_{n}
$$
For $x \geqslant 0$, we then have
(A.1) $\sum_{1 \leqslant n \leqslant x} a_{n} f(n)=\mathrm{M}{a}(x) f(x)-\int{1}^{x} \mathrm{M}{a}(t) f^{\prime}(t) d t$. If $\mathrm{M}{a}(x) f(x)$ tends to 0 as $x \rightarrow+\infty$, then we have
$$
\sum_{n \geqslant 1} a_{n} f(n)=-\int_{1}^{+\infty} \mathrm{M}_{a}(t) f^{\prime}(t) d t
$$
provided either the series or the integral converges absolutely, in which case both of them do.
Using this formula, one can exploit known information (upper bounds or asymptotic formulas) concerning the summation function $\mathrm{M}{a}$, typically when the sequence $\left(a{n}\right)$ is irregular, in order to understand the summation function for $a_{n} f(n)$ for many sufficiently regular functions $f$.
The reader should attempt to write a proof of this lemma, but we give the details for completeness.
Proof. Let $\mathrm{N} \geqslant 0$ be the integer such that $\mathrm{N} \leqslant x<\mathrm{N}+1$. We have
$$
\sum_{1 \leqslant n \leqslant x} a_{n} f(n)=\sum_{1 \leqslant n \leqslant \mathrm{~N}} a_{n} f(n)
$$
By the usual integration by parts formula, we then note that
$$
\mathrm{M}{a}(x) f(x)-\int{1}^{x} \mathrm{M}{a}(t) f^{\prime}(t) d t=\mathrm{M}{a}(\mathrm{~N}) f(\mathrm{~N})-\int_{1}^{\mathrm{N}} \mathrm{M}{a}(t) f^{\prime}(t) d t $$ (because $\mathrm{M}{a}$ is constant on the interval $\mathrm{N} \leqslant t \leqslant x$ ). We therefore reduce to the case $x=$ $\mathrm{N}$. We then have
$$
\begin{aligned}
\sum_{n \leqslant \mathrm{~N}} a_{n} f(n) &=\sum_{1 \leqslant n \leqslant \mathrm{~N}}\left(\mathrm{M}{a}(n)-\mathrm{M}{a}(n-1)\right) f(n) \
&=\sum_{1 \leqslant n \leqslant \mathrm{~N}} \mathrm{M}{a}(n) f(n)-\sum{0 \leqslant n \leqslant \mathrm{~N}-1} \mathrm{M}{a}(n) f(n+1) \ &=\mathrm{M}{a}(\mathrm{~N}) f(\mathrm{~N})+\sum_{1 \leqslant n \leqslant \mathrm{~N}-1} \mathrm{M}{a}(n)(f(n)-f(n+1)) \ &=\mathrm{M}{a}(\mathrm{~N}) f(\mathrm{~N})-\sum_{1 \leqslant n \leqslant \mathrm{~N}-1} \mathrm{M}{a}(n) \int{n}^{n+1} f^{\prime}(t) d t \
&=\mathrm{M}{a}(\mathrm{~N}) f(\mathrm{~N})-\int{1}^{\mathrm{N}} \mathrm{M}{a}(t) f^{\prime}(t) d t \end{aligned} $$ which concludes the first part of the lemma. The last assertion follows immediately by letting $x \rightarrow+\infty$, in view of the assumption on the limit of $\mathrm{M}{a}(x) f(x)$.
A.2. The logarithm
In Chapters 3 and 4, we sometimes use the logarithm for complex numbers. Since this is not a globally defined function on $\mathrm{C}^{\times}$, we clarify here what we mean.
DEFINITION A.2.1. Let $z \in \mathrm{C}$ be a complex number with $|z|<1$. We define
$$
\log (1-z)=-\sum_{k \geqslant 1} \frac{z^{k}}{k}
$$
Proposition A.2.2. (1) For any complex number z such that $|z|<1$, we have $e^{\log (1-z)}=1-z$
(2) Let $\left(z_{n}\right){n \geqslant 1}$ be a sequence of complex numbers such that $\left|z{n}\right|<1$. If
$$
\sum_{n}\left|z_{n}\right|<+\infty
$$
解析数论非常频繁地使用“分部求和”,这是一种分部积分的离散形式。我们说明我们使用的版本。
LEMMA A.1.1(按部分求和)。令 $\left(a_{n}\right){n \geqslant 1}$ 为复数序列且 $f:\left[0,+\infty\left[\rightarrow \mathrm{C}\right .\right.$ $\mathrm{C}^{1}$ 类的函数。对于所有 $x \geqslant 0$,定义 $$ \mathrm{M}{a}(x)=\sum_{1 \leqslant n \leqslant x} a_{n}
$$
对于 $x \geqslant 0$,我们有
(A.1) $\sum_{1 \leqslant n \leqslant x} a_{n} f(n)=\mathrm{M}{a}(x) f(x)-\int{1}^{ x} \mathrm{M}{a}(t) f^{\prime}(t) dt$。 如果 $\mathrm{M}{a}(x) f(x)$ 随着 $x \rightarrow+\infty$ 趋向于 0,那么我们有
$$
\sum_{n \geqslant 1} a_{n} f(n)=-\int_{1}^{+\infty} \mathrm{M}_{a}(t) f^{\prime}(t) dt
$$
前提是级数或积分绝对收敛,在这种情况下它们都收敛。
使用这个公式,可以利用关于求和函数 $\mathrm{M}{a}$ 的已知信息(上限或渐近公式),通常当序列 $\left(a{n}\right)$ 不规则时, 为了理解许多足够规则的函数 $f$ 的 $a_{n} f(n)$ 的求和函数。
读者应该尝试写出这个引理的证明,但为了完整起见,我们给出了细节。
证明。令 $\mathrm{N} \geqslant 0$ 为整数,使得 $\mathrm{N} \leqslant x<\mathrm{N}+1$。我们有
$$
\sum_{1 \leqslant n \leqslant x} a_{n} f(n)=\sum_{1 \leqslant n \leqslant \mathrm{~N}} a_{n} f(n)
$$
通过通常的按部分积分公式,我们注意到
$$
\mathrm{M}{a}(x) f(x)-\int{1}^{x} \mathrm{M}{a}(t) f^{\prime}(t) dt=\ mathrm{M}{a}(\mathrm{~N}) f(\mathrm{~N})-\int_{1}^{\mathrm{N}} \mathrm{M}{a}(t ) f^{\素数}(t) dt $$ (因为 $\mathrm{M}{a}$ 在区间 $\mathrm{N} \leqslant t \leqslant x$ 上是常数)。因此我们简化为 $x=$$\mathrm{N}$ 的情况。然后我们有
$$
\开始{对齐}
\sum_{n \leqslant \mathrm{~N}} a_{n} f(n) &=\sum_{1 \leqslant n \leqslant \mathrm{~N}}\left(\mathrm{M}{a }(n)-\mathrm{M}{a}(n-1)\right) f(n) \
&=\sum_{1 \leqslant n \leqslant \mathrm{~N}} \mathrm{M}{a}(n) f(n)-\sum{0 \leqslant n \leqslant \mathrm{~N} -1} \mathrm{M}{a}(n) f(n+1) \ &=\mathrm{M}{a}(\mathrm{~N}) f(\mathrm{~N})+\sum_{1 \leqslant n \leqslant \mathrm{~N}-1} \mathrm{ M}{a}(n)(f(n)-f(n+1)) \ &=\mathrm{M}{a}(\mathrm{~N}) f(\mathrm{~N})-\sum_{1 \leqslant n \leqslant \mathrm{~N}-1} \mathrm{ M}{a}(n) \int{n}^{n+1} f^{\prime}(t) dt \
&=\mathrm{M}{a}(\mathrm{~N}) f(\mathrm{~N})-\int{1}^{\mathrm{N}} \mathrm{M}{a }(t) f^{\prime}(t) dt \end{对齐} $$ 这结束了引理的第一部分。鉴于对 $\mathrm{M}{a}(x) f(x)$ 极限的假设,最后一个断言通过让 $x \rightarrow+\infty$ 紧随其后。
A2。对数
在第 3 章和第 4 章中,我们有时对复数使用对数。由于这不是 $\mathrm{C}^{\times}$ 上的全局定义函数,因此我们在此澄清我们的意思。
定义 A.2.1。令$z \in \mathrm{C}$ 是一个复数,$|z|<1$。我们定义
$$
\log (1-z)=-\sum_{k \geqslant 1} \frac{z^{k}}{k}
$$
命题 A.2.2。 (1) 对于任何复数 z 使得 $|z|<1$,我们有 $e^{\log (1-z)}=1-z$
(2) 令$\left(z_{n}\right){n \geqslant 1}$ 是一个复数序列,使得$\left|z{n}\right|<1$。如果
$$
\sum_{n}\left|z_{n}\right|<+\infty
$$
数论代写
数论是纯粹数学的分支之一,主要研究整数的性质。整数可以是方程式的解(丢番图方程)。有些解析函数(像黎曼ζ函数)中包括了一些整数、质数的性质,透过这些函数也可以了解一些数论的问题。透过数论也可以建立实数和有理数之间的关系,并且用有理数来逼近实数(丢番图逼近)。
按研究方法来看,数论大致可分为初等数论和高等数论。初等数论是用初等方法研究的数论,它的研究方法本质上说,就是利用整数环的整除性质,主要包括整除理论、同余理论、连分数理论。高等数论则包括了更为深刻的数学研究工具。它大致包括代数数论、解析数论、计算数论等等。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
在中世纪时,除了1175年至1200年住在北非和君士坦丁堡的斐波那契有关等差数列的研究外,西欧在数论上没有什么进展。
数论中期主要指15-16世纪到19世纪,是由费马、梅森、欧拉、高斯、勒让德、黎曼、希尔伯特等人发展的。最早的发展是在文艺复兴的末期,对于古希腊著作的重新研究。主要的成因是因为丢番图的《算术》(Arithmetica)一书的校正及翻译为拉丁文,早在1575年Xylander曾试图翻译,但不成功,后来才由Bachet在1621年翻译完成。
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。