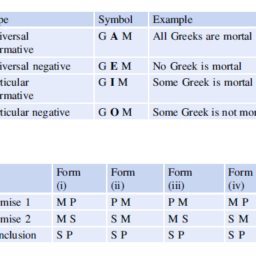
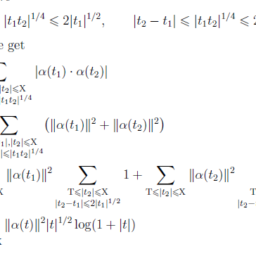运筹学(Operation)是近代应用数学的一个分支。它把具体的问题进行数学抽象,然后用像是统计学、数学模型和算法等方法加以解决,以此来寻找复杂问题中的最佳或近似最佳的解答。
作为专业的留学生服务机构,Assignmentexpert™多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于论文代写,A作业代写,Dissertation代写,Report代写,Paper代写,Presentation代写,网课代修等等。为涵盖高中,本科,研究生等海外留学生提供辅导服务,辅导学科包括数学,物理,统计,化学,金融,经济学,会计学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
运筹学代写
There are several remaining important issues concerning interior-point algorithms for linear programs. The first issue involves termination. Unlike the simplex method which terminates with an exact solution, interior-point algorithms are continuous optimization algorithms that generate an infinite solution sequence converging to an optimal solution. If the data of a particular problem are integral or rational, an argument is made that, after the worst-case time bound, an exact solution can be rounded from the latest approximate solution. Several questions arise. First, under the real number computation model (that is, the data consists of real numbers), how can we terminate at an exact solution? Second, regardless of the data’s status, is there a practical test, which can be computed cost-effectively during the iterative process, to identify an exact solution so that the algorithm can be terminated before the worse-case time bound? Here, by exact solution we mean one that could be found using exact arithmetic, such as the solution of a system of linear equations, which in $n$.
The second issue involves initialization. Almost all interior-point algorithms require the regularity assumption that $\stackrel{\mathscr{F}}{\mathcal{F}} \neq \emptyset$. What is to be done if this is not true? A related issue is that interior-point algorithms have to start at a strictly feasible point near the central path.
*Termination
Complexity bounds for interior-point algorithms generally depend on an $\varepsilon$ which must be zero in order to obtain an exact optimal solution. Sometimes it is advantageous to employ an early termination or rounding method while $\varepsilon$ is still moderately large. There are five basic approaches.
- A “purification” procedure finds a feasible corner whose objective value is at least as good as the current interior point. This can be accomplished in strongly polynomial time (that is, the complexity bound is a polynomial only in the dimensions $m$ and $n$ ). One difficulty is that there may be many non-optimal steps for difficult problems.
- A second method seeks to identify an optimal basis. It has been shown that if the linear program is nondegenerate, the unique optimal basis may be identified early. The procedure seems to work well for some problems but it has difficulty if the probler
- The third approach is to slightly perturb the data such that the new program is nondegenerate and its optimal basis remains one of the optimal bases of the original program. There are questions about how and when to perturb the data
5.7 Termination and Initialization
155
Fig. $5.5$ Illustration of the projection of an interior point onto the optimal face
during the iterative process, decisions which can significantly affect the success of the effort. – The fourth approach is to guess the optimal face and find a feasible solution on that face. It consists of two phases: the first phase uses interior-point algorithms to identify the complementarity partition $\left(P^{}, Z^{}\right.$ ) (see Exercise 6$)$, and the second phase adapts the simplex method to find an optimal primal (or dual) basic solution and one can use ( $\left.P^{}, Z^{}\right)$ as a starting base for the second phase. This method is often called the crossover method. It is guaranteed to work in finite time and is implemented in several popular linear programming software packages. The fifth approach is to guess the optimal face and project the current interior point onto the interior of the optimal face. See Fig. $5.5$. The termination criterion is guaranteed to work in finite time. The fourth and fifth methods above are based on the fact that (as observed in practice and subsequently proved) many interior-point algorithms for linear programming generate solution sequences that converge to a strictly complementary solution or an interior solution on the optimal face; see Exercise 8 .
关于线性规划的内点算法,还有几个重要的问题。第一个问题涉及终止。与以精确解终止的单纯形法不同,内点算法是连续优化算法,可生成收敛到最优解的无限解序列。如果特定问题的数据是整数或有理数,则提出一个论点,即在最坏情况的时间界限之后,可以从最新的近似解四舍五入一个精确解。出现了几个问题。首先,在实数计算模型下(即数据由实数组成),我们如何终止于精确解?其次,不管数据的状态如何,是否有一个实际测试,可以在迭代过程中经济高效地计算,以确定一个精确的解决方案,以便在最坏情况的时间限制之前终止算法?在这里,我们所说的精确解是指可以使用精确算术找到的解,例如线性方程组的解,其单位为 $n$。
第二个问题涉及初始化。几乎所有内点算法都需要 $\stackrel{\mathscr{F}}{\mathcal{F}} \neq \emptyset$ 的正则性假设。如果这不是真的,该怎么办?一个相关的问题是内点算法必须从靠近中心路径的严格可行点开始。
*终止
内点算法的复杂性界限通常取决于$\varepsilon$,它必须为零才能获得精确的最优解。有时在 $\varepsilon$ 仍然中等大时采用提前终止或舍入方法是有利的。有五种基本方法。
- “净化”程序找到一个可行的角点,其目标值至少与当前内部点一样好。这可以在强多项式时间内完成(也就是说,复杂度界限是仅在维度 $m$ 和 $n$ 中的多项式)。一个困难是对于困难的问题可能有许多非最佳步骤。
- 第二种方法寻求确定最佳基础。已经表明,如果线性程序是非退化的,则可以及早识别唯一的最优基。该程序似乎可以很好地解决某些问题,但如果出现问题,则有困难
- 第三种方法是稍微扰动数据,使新程序是非退化的,并且其最优基仍然是原始程序的最优基之一。关于如何以及何时扰乱数据存在问题
5.7 终止和初始化
155
Fig. $5.5$ 内点投影到最优面的示意图
在迭代过程中,可以显着影响工作成功的决策。 – 第四种方法是猜测最佳人脸并在该人脸上找到可行的解决方案。它由两个阶段组成:第一阶段使用内点算法来识别互补分区 $\left(P^{}, Z^{}\right.$)(参见练习 6$)$,第二阶段phase 采用单纯形法来找到最优的原始(或对偶)基本解,并且可以使用 ($\left.P^{}, Z^{}\right)$ 作为第二阶段的起始基础。这种方法通常称为交叉法。它保证在有限时间内工作,并在几个流行的线性编程软件包中实现。第五种方法是猜测最优人脸并将当前内部点投影到最优人脸内部。见图 5.5 美元。终止准则保证在有限时间内起作用。上面的第四和第五种方法是基于这样一个事实(如在实践中观察到并随后证明)许多用于线性规划的内点算法生成的解序列收敛到一个严格互补的解或最优面上的一个内解;见练习 8。
运筹学代考

什么是运筹学代写
运筹学(OR)是一种解决问题和决策的分析方法,在组织管理中很有用。在运筹学中,问题被分解为基本组成部分,然后通过数学分析按定义的步骤解决。
运筹学的过程大致可以分为以下几个步骤:
- 确定需要解决的问题。
- 围绕问题构建一个类似于现实世界和变量的模型。
- 使用模型得出问题的解决方案。
- 在模型上测试每个解决方案并分析其成功。
- 实施解决实际问题的方法。
与运筹学交叉的学科包括统计分析、管理科学、博弈论、优化理论、人工智能和复杂网络分析。所有这些学科的目标都是解决某一个现实中出现的复杂问题或者用数学的方法为决策提供指导。 运筹学的概念是在二战期间由参与战争的数学家们提出的。二战后,他们意识到在运筹学中使用的技术也可以被应用于解决商业、政府和社会中的问题。
运筹学代写的三个特点
所有运筹学解决实际问题的过程中都具有三个主要特征:
- 优化——运筹学的目的是在给定的条件下达到某一机器或者模型的最佳性能。优化还涉及比较不同选项和缩小潜在最佳选项的范围。
- 模拟—— 这涉及构建模型,以便在应用解决方案刀具体的复杂大规模问题之前之前尝试和测试简单模型的解决方案。
- 概率和统计——这包括使用数学算法和数据挖掘来发现有用的信息和潜在的风险,做出有效的预测并测试可能的解决方法。
运筹学领域提供了比普通软件和数据分析工具更强大的决策方法。此外,运筹学可以根据特定的业务流程或用例进行定制,以确定哪些技术最适合解决问题。
运筹学可以应用于各种活动,比如:计划和时间管理(Planning and Time Management),城乡规划(Urban and Rural Planning),企业资源计划(ERP)与供应链管理(Supply Chain Management)等等。 如有代写代考需求,欢迎同学们联系Assignmentexpert™,我们期待为你服务!