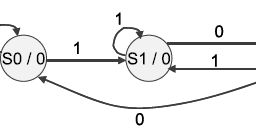
复杂性理论(complexity theory)是理论计算机科学和数学的一个分支,它致力于将可计算问题根据它们本身的复杂性分类,以及将这些类别联系起来。 一个可计算问题被认为是一个原则上可以用计算机解决的问题,亦即这个问题可以用一系列机械的数学步骤解决,例如算法。
作为专业的留学生服务机构,Assignmentexpert™多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于论文代写,A作业代写,Dissertation代写,Report代写,Paper代写,Presentation代写,网课代修等等。为涵盖高中,本科,研究生等海外留学生提供辅导服务,辅导学科包括数学,物理,统计,化学,金融,经济学,会计学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
运筹学代写
Complexity theory is arguably the foundation for analysis of computer algorithms. The goal of the theory is twofold: to develop criteria for measuring the effectiveness of various algorithms (and thus, be able to compare algorithms using these criteria), and to assess the inherent difficulty of various problems.
The term complexity refers to the amount of resources required by a computation. In this chapter we focus on a particular resource, namely, computing time. In complexity theory, however, one is not interested in the execution time of a program implemented in a particular programming language, running on a particular computer over a particular input. This involves too many contingent factors. requirements.
Roughly speaking, to do so one needs to define:
- a notion of input size,
- a set of basic operations, and
- a cost for each basic operation.
The last two allow one to associate a cost of a computation. If $x$ is any input, the cost $C(x)$ of the computation with input $x$ is the sum of the costs of all the basic operations performed during this computation.
Let $\mathcal{A}$ be an algorithm and $\mathcal{J}{n}$ be the set of all its inputs having size $n$. The worst-case cost function of $\mathcal{A}$ is the function $T{\mathscr{A}}^{w}$ defined by
$$
T_{\mathcal{A}}^{w}(n)=\sup {x \in \mathcal{I}{n}} C(x) .
$$
If there is a probability structure on $\mathcal{J}{n}$ it is possible to define the average-case cost function $T{\mathscr{A}}^{a}$ given by
$$
T_{\mathcal{A}^{a}}(n)=\mathrm{E}{n}(C(x)) $$ where $\mathrm{E}{n}$ is the expectation over $\mathcal{J}_{n}$. However, the average is usually more difficult to find, and there is of course the issue of what probabilities to assign.
We now discuss how the objects in the three items above are selected. The selection of a set of basic operations is generally easy. For the algorithms we consider in this chapter, the obvious choice is the set ${+,-, \times, /, \leq}$ of the four arithmetic operations and the comparison. Selecting a notion of input size and a cost for the basic operations depends on the kind of data dealt with by the algorithm. require a variable amount.
Examples of the first are fixed-precision floating-point numbers, stored in a fixed amount of memory (usually 32 or 64 bits). For this kind of data the size of an element is usually taken to be 1 and consequently to have unit size per number.
132
5 Interior-Point Methods
Examples of the second are integer numbers which require a number of bits approximately equal to the logarithm of their absolute value. This (base 2) logarithm is usually referred to as the bit-size of the integer. Similar ideas apply for rational numbers.
Let $A$ be some kind of data and $\mathbf{x}=\left(x_{1}, \ldots, x_{n}\right) \in A^{n}$. If $A$ is of the first kind above then we define $\operatorname{size}(\mathbf{x})=n$. Otherwise, we define $\operatorname{size}(\mathbf{x})=\sum_{i=1}^{n}$ bit-size $\left(x_{i}\right)$.
The cost of operating on two unit size numbers is taken to be 1 and is called the unit cost. In the bit-size case, the cost of operating on two numbers is the product of their bit-sizes (for multiplications and divisions) or their maximum (for additions, subtractions, and comparisons).
The consideration of integer or rational data with their associated bit-size and bit cost for the arithmetic operations is usually referred to as the Turing model of computation. The consideration of idealized reals with unit size and unit cost is today referred as the real number arithmetic model. When comparing algorithms, one should
A basic concept related to both models of computation is that of polynomial time.
A basic concept related to both models of computation is that of polynomial time. An algorithm $\mathcal{A}$ is said to be a polynomial time algorithm if $T_{\mathcal{A}}(n)$ is bounded above by a polynomial. A problem can be solved in polynomial time if there is a polynomial time algorithm solving the problem.
is defined similarly, replacing $T_{\mathcal{A}}$ by $T_{\mathscr{A}}^{a}$. The notion of polynomial time is usually taken as the formalization of efficiency in complexity theory.
Elements of Complexity Theory复杂度理论代写
复杂性理论可以说是分析计算机算法的基础。该理论的目标是双重的:制定衡量各种算法有效性的标准(因此,能够使用这些标准比较算法),以及评估各种问题的内在难度。
术语复杂性是指计算所需的资源量。在本章中,我们关注一个特定的资源,即计算时间。然而,在复杂性理论中,人们对以特定编程语言实现、在特定计算机上通过特定输入运行的程序的执行时间不感兴趣。这涉及到太多的偶然因素。要求。
粗略地说,要做到这一点,需要定义:
- 输入大小的概念,
- 一组基本操作,以及
- 每个基本操作的成本。
最后两个允许将计算成本关联起来。如果 $x$ 是任何输入,则输入 $x$ 的计算成本 $C(x)$ 是在此计算期间执行的所有基本操作的成本总和。
令 $\mathcal{A}$ 是一个算法,$\mathcal{J}{n}$ 是它所有大小为 $n$ 的输入的集合。 $\mathcal{A}$ 的最坏情况成本函数是由下式定义的函数 $T{\mathscr{A}}^{w}$
$$
T_{\mathcal{A}}^{w}(n)=\sup {x \in \mathcal{I}{n}} C(x) 。
$$
如果 $\mathcal{J}{n}$ 上存在概率结构,则可以定义平均情况成本函数 $T{\mathscr{A}}^{a}$
$$
T_{\mathcal{A}^{a}}(n)=\mathrm{E}{n}(C(x)) $$ 其中 $\mathrm{E}{n}$ 是对 $\mathcal{J}_{n}$ 的期望。然而,平均值通常更难找到,当然还有分配什么概率的问题。
我们现在讨论如何选择上面三个项目中的对象。一组基本操作的选择通常很容易。对于本章我们考虑的算法,显而易见的选择是四个算术运算的集合${+,-,\times, /, \leq}$ 和比较。选择输入大小的概念和基本操作的成本取决于算法处理的数据类型。需要可变数量。
第一个例子是固定精度浮点数,存储在固定数量的内存中(通常是 32 位或 64 位)。对于这种数据,元素的大小通常取为 1,因此每个数字具有单位大小。
132
5 内点法
第二种的例子是整数,它需要的位数大约等于它们的绝对值的对数。这个(以 2 为底)对数通常称为整数的位大小。类似的想法也适用于有理数。
令 $A$ 是某种数据,$\mathbf{x}=\left(x_{1}, \ldots, x_{n}\right) \in A^{n}$。如果 $A$ 是上面的第一种,那么我们定义 $\operatorname{size}(\mathbf{x})=n$。否则,我们定义 $\operatorname{size}(\mathbf{x})=\sum_{i=1}^{n}$ 位大小 $\left(x_{i}\right)$。
对两个单位尺寸数进行操作的成本取为 1,称为单位成本。在位大小的情况下,对两个数字进行运算的成本是它们的位大小(用于乘法和除法)或它们的最大值(用于加法、减法和比较)的乘积。
考虑整数或有理数据及其相关的位大小和算术运算的位成本通常称为图灵计算模型。考虑具有单位大小和单位成本的理想实数今天被称为实数算术模型。在比较算法时,应该
与这两种计算模型相关的一个基本概念是多项式时间。
与这两种计算模型相关的一个基本概念是多项式时间。如果 $T_{\mathcal{A}}(n)$ 以多项式为界,则算法 $\mathcal{A}$ 称为多项式时间算法。如果存在解决问题的多项式时间算法,则可以在多项式时间内解决问题。
定义类似,将 $T_{\mathcal{A}}$ 替换为 $T_{\mathscr{A}}^{a}$。多项式时间的概念通常被视为复杂性理论中效率的形式化。
运筹学代考

什么是运筹学代写
运筹学(OR)是一种解决问题和决策的分析方法,在组织管理中很有用。在运筹学中,问题被分解为基本组成部分,然后通过数学分析按定义的步骤解决。
运筹学的过程大致可以分为以下几个步骤:
- 确定需要解决的问题。
- 围绕问题构建一个类似于现实世界和变量的模型。
- 使用模型得出问题的解决方案。
- 在模型上测试每个解决方案并分析其成功。
- 实施解决实际问题的方法。
与运筹学交叉的学科包括统计分析、管理科学、博弈论、优化理论、人工智能和复杂网络分析。所有这些学科的目标都是解决某一个现实中出现的复杂问题或者用数学的方法为决策提供指导。 运筹学的概念是在二战期间由参与战争的数学家们提出的。二战后,他们意识到在运筹学中使用的技术也可以被应用于解决商业、政府和社会中的问题。
运筹学代写的三个特点
所有运筹学解决实际问题的过程中都具有三个主要特征:
- 优化——运筹学的目的是在给定的条件下达到某一机器或者模型的最佳性能。优化还涉及比较不同选项和缩小潜在最佳选项的范围。
- 模拟—— 这涉及构建模型,以便在应用解决方案刀具体的复杂大规模问题之前之前尝试和测试简单模型的解决方案。
- 概率和统计——这包括使用数学算法和数据挖掘来发现有用的信息和潜在的风险,做出有效的预测并测试可能的解决方法。
运筹学领域提供了比普通软件和数据分析工具更强大的决策方法。此外,运筹学可以根据特定的业务流程或用例进行定制,以确定哪些技术最适合解决问题。
运筹学可以应用于各种活动,比如:计划和时间管理(Planning and Time Management),城乡规划(Urban and Rural Planning),企业资源计划(ERP)与供应链管理(Supply Chain Management)等等。 如有代写代考需求,欢迎同学们联系Assignmentexpert™,我们期待为你服务!