my-assignmentexpert™ Economics 经济学作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 $100 \%$ 原创。my-assignmentexpert™, 最高质量的ECON经济学作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此经济作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济代写服务。我们的专家在经济学 代写方面经验极为丰富,各种economics相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 微观经济学
- 货币银行学
- 数量经济学
- 宏观经济学
- 经济统计学
- 经济学理论
- 商务经济学
- 计量经济学
- 金融经济学
- 国际经济学
- 健康经济学
- 劳动经济学
Solutions functions and solution correspondences|Econ经济作业代写Economics代考
Ideally, solution concepts are described both algorithmically and axiomatically. An algorithm is some kind of mathematical procedure (a more or less simple function) that tells us how to derive payoffs from the coalition functions. Consider, for example, these four solution concepts in algorithmic form:
- player 1 obtains $v(N)$ and the other players obtain 0 ,
- every player gets 100 ,
- every player gets $v(N) / n$,
- every player $i$ ‘s payoff set is given by $[v({i}), v(N)]$ (which may be the empty set).
Alternatively, solution concepts can be defined by axioms. For example, axioms might demand that - all the players obtain the same payoff,
- no more than $v(N)$ is to be distributed among the players,
- player 1 is to get twice the payoff obtained by player 2 ,
- the names of players are irrelevant,
- every player gets $v(N)-v(N \backslash{i})$.
Axioms pin down the players’ payoffs, more or less. Axioms may also make contradictory demands. We present prominent axioms in the following sections.
Solution correspondence: Pareto efficiency.|ECON经济作业代写ECONOMICS代考
4.2. Solution correspondence: Pareto efficiency. Arguably, Pareto efficiency is the single most often applied solution concept in economics rivaled only by the Nash equilibrium from non-cooperative game theory. For the gloves game, Pareto efficiency is defined by
$$
\sum_{i \in N} x_{i}=v_{L, R}(N) .
$$
Thus, the sum of all payoffs is equal to the number of glove pairs. It is instructive to write this equality as two inequalities:
$$
\begin{aligned}
&\sum_{i \in N} x_{i} \leq v_{L, R}(N) \text { (feasibility) and } \
&\sum_{i \in N} x_{i} \geq v_{L, R}(N) \text { (the grand coalition cannot block } x \text { ). }
\end{aligned}
$$
According to the first inequality, the players cannot distribute more than they (all together) can “produce”. This is the requirement of feasibility.
$$
Solution correspondence: The core.|ECON经济作业代写ECONOMICS代考
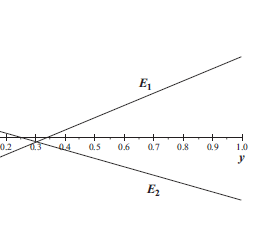
The core is a stricter concept than Pareto efficiency. It demands that no coalition (not just the grand coalition) can block any of its payoff vectors. Let us consider the gloves game for $L={1}$ and $R={2}$. By Pareto efficiency, we can restrict attention to those payoff vectors $x=\left(x_{1}, x_{2}\right)$ that fulfill $x_{1}+x_{2}=1$. Furthermore, $x$ may not be blocked by one-man coalitions:
$$
\begin{aligned}
&x_{1} \geq v_{L, R}({1})=0 \text { and } \
&x_{2} \geq v_{L, R}({2})=0
\end{aligned}
$$
Hence, the core is the set of payoff vectors $x=\left(x_{1}, x_{2}\right)$ obeying
$$
x_{1}+x_{2}=1, x_{1} \geq 0, x_{2} \geq 0 .
$$
Are we not forgetting about $K=\emptyset$ ? Let us check
$$
\sum_{i \in \emptyset} x_{i} \geq v_{L, R}(\emptyset)
$$
Since there is no $i$ from $\emptyset$ (otherwise $\emptyset$ would not be the empty set), the sum $\sum_{i \in \emptyset} x_{i}$ has no summands and is equal to zero. Since all coalition functions have worth zero for the empty set, we find $\sum_{i \in \emptyset} x_{i}=0=v_{L, R}(\emptyset)$ for the gloves game and also for any coalition function.

SOLUTIONS FUNCTIONS AND SOLUTION CORRESPONDENCES|ECON经济作业代写ECONOMICS代考
理想情况下,解决方案的概念是用算法和公理来描述的。算法是某种数学过程(或多或少简单的函数),它告诉我们如何从联合函数中获得收益。例如,考虑以下四个算法形式的解决方案概念:
- 玩家 1 获得v(ñ)其他玩家获得 0 ,
- 每个玩家得到 100 ,
- 每个玩家都得到v(ñ)/n,
- 每个玩家一世的收益集由下式给出[v(一世),v(ñ)](可能是空集)。
或者,解决方案概念可以由公理定义。例如,公理可能要求 - 所有玩家获得相同的收益,
- 不超过v(ñ)将分发给玩家,
- 玩家 1 将获得玩家 2 的两倍收益,
- 球员的名字无关紧要,
- 每个玩家都得到v(ñ)−v(ñ∖一世).
公理或多或少地确定了玩家的收益。公理也可能提出相互矛盾的要求。我们将在以下部分中介绍突出的公理。
SOLUTION CORRESPONDENCE: PARETO EFFICIENCY.|ECON经济作业代写ECONOMICS代考
4.2. 解对应:帕累托效率。可以说,帕累托效率是经济学中最常用的解决方案概念,仅可与非合作博弈论中的纳什均衡相媲美。对于手套博弈,帕累托效率定义为
∑一世∈ñX一世=v一世,R(ñ).
因此,所有收益的总和等于手套对的数量。把这个等式写成两个不等式是有启发性的:
∑一世∈ñX一世≤v一世,R(ñ) (可行性)和 ∑一世∈ñX一世≥v一世,R(ñ) (大联盟无法阻止 X ).
根据第一个不等式,玩家分配的数量不能超过他们(全部)“生产”的数量。这是可行性的要求。
$$
SOLUTION CORRESPONDENCE: THE CORE.|ECON经济作业代写ECONOMICS代考
核心是比帕累托效率更严格的概念。它要求任何联盟(不仅仅是大联盟)都不能阻止其任何收益向量。让我们考虑一下手套游戏一世=1和R=2. 通过帕累托效率,我们可以将注意力限制在那些支付向量上X=(X1,X2)满足X1+X2=1. 此外,X不能被单人联盟阻止:
X1≥v一世,R(1)=0 和 X2≥v一世,R(2)=0
因此,核心是一组支付向量X=(X1,X2)服从
X1+X2=1,X1≥0,X2≥0.
难道我们没有忘记到=∅? 让我们检查一下
∑一世∈∅X一世≥v一世,R(∅)
由于没有一世从∅(否则∅不会是空集),总和∑一世∈∅X一世没有和并且等于零。由于空集的所有联合函数的值为零,我们发现∑一世∈∅X一世=0=v一世,R(∅)对于手套游戏以及任何联盟功能。

matlab代写请认准UprivateTA™.
经济代写
计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写