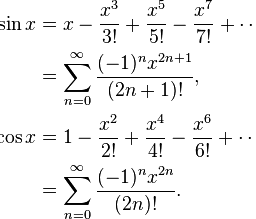微积分(Calculus),数学概念,是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科,内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法
my-assignmentexpert™ 微积分calculus作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的微积分calculus作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微积分calculus作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的微积分calculus代写服务。我们的专家在微积分calculus学 代写方面经验极为丰富,各种微积分calculus相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 单变量微积分
- 多变量微积分
- 傅里叶级数
- 黎曼积分
- ODE
- 微分学

微积分代考calculus代写|Definition and Some Basic Results
Convention: When we say that $f$ is continuous at a point $x_{0} \in \mathbb{R}$, we mean that $f$ is defined on an interval containing $x_{0}$ and $f$ is continuous at $x_{0}$.
Example 2.2.1 Let $f(x)=a_{0}+a_{1} x+\cdots a_{k} x^{k}$ for some $a_{0}, a_{1}, \ldots, a_{k}$ in $\mathbb{R}$ and $k \in \mathbb{N}$. We know (cf. Example 2.1.8) that, for any $x_{0} \in \mathbb{R}$,
$$
\lim {x \rightarrow x{0}} f(x)=f\left(x_{0}\right) .
$$
Hence, by Theorem 2.2.1, $f$ is continuous at every $x_{0} \in \mathbb{R}$ (Fig. 2.9).
Example 2.2.2 Let $f:[-1,1] \rightarrow \mathbb{R}$ be as in Example 2.1.3, i.e.,
$$
f(x)=\left{\begin{array}{l}
0,-1 \leq x \leq 0 \
1,0<x \leq 1
\end{array}\right.
$$
We have seen that $\lim {x \rightarrow 0} f(x)$ does not exist. Hence, by Theorem 2.2.1, $f$ is not continuous at 0 . Example 2.2.3 We have seen in Examples 2.1.10 and 2.1.11 that $$ \lim {x \rightarrow 0} \sin x=0, \quad \lim {x \rightarrow 0} \cos x=1, \quad \lim {x \rightarrow 0} \frac{\sin x}{x}=1 .
$$
微积分代考CALCULUS代写|Some More Examples
Example 2.2.6 We already observed in Example 2.2.3 that the functions $f, g, h$ defined by
$$
f(x)=\sin x, \quad g(x)=\cos x, \quad h(x)= \begin{cases}\frac{\sin x}{x}, & x \neq 0, \ 1, & x=0\end{cases}
$$
are continuous at 0 . Now, we show that they are continuous at every point in $\mathbb{R}$.
Note that for $x, y \in \mathbb{R}$,
$$
\sin x-\sin y=2 \sin \left(\frac{x-y}{2}\right) \cos \left(\frac{x+y}{2}\right)
$$
so that
$$
|\sin x-\sin y| \leq|x-y| \quad \forall x, y \in \mathbb{R}
$$
Hence, for every $\varepsilon>0$ and for every $x_{0} \in \mathbb{R}$,
$$
x \in \mathbb{R}, \quad\left|x-x_{0}\right|<\varepsilon \Rightarrow\left|\sin x-\sin x_{0}\right|<\varepsilon .
$$
Thus, $f$ is continuous at every point in $\mathbb{R}$. Since $\cos x=1-2 \sin ^{2}(x / 2), x \in \mathbb{R}$, it also follows that $g$ is continuous at every point in $\mathbb{R}$. Now, let $x_{0} \neq 0$. Then the continuity of $h$ at $x_{0}$ follows from Theorem 2.2.6, since $h=f / f_{0}$ where $f_{0}(x)=x$ in nonzero in a neighbourhood of $x_{0}$.
微积分代考CALCULUS代写|Some Properties of Continuous Functions
Recall that a subset $S$ of $\mathbb{R}$ is said to be bounded if there exists $M>0$ such that $|s| \leq M$ for all $s \in S$, and a set which is not bounded is called an unbounded set. Recall also that if $S$ is a bounded subset of $\mathbb{R}$, then $S$ has the infimum and the supremum, not necessarily in $S$.
For $S \subseteq \mathbb{R}$, we have the following:
- Suppose $S$ is bounded, and say $\alpha:=\inf S$ and $\beta:=\sup S$. Then there exist sequences $\left(s_{n}\right)$ and $\left(t_{n}\right)$ in $S$ such that $s_{n} \rightarrow \alpha$ and $t_{n} \rightarrow \beta$.
- $S$ is unbounded if and only if there exists a sequence $\left(s_{n}\right)$ in $S$ which is unbounded.
- $S$ is unbounded if and only if there exists a sequence $\left(s_{n}\right)$ in $S$ such that $\left|s_{n}\right| \rightarrow \infty$ as $n \rightarrow \infty$.
- If $\left(s_{n}\right)$ is a sequence in $S$ which is unbounded, then there exists a subsequence $\left(s_{k_{n}}\right)$ of $\left(s_{n}\right)$ such that $\left|s_{k_{n}}\right| \rightarrow \infty$ as $n \rightarrow \infty$.
- If $\left(s_{n}\right)$ is a sequence in $S$ such that $\left|s_{n}\right| \rightarrow \infty$ as $n \rightarrow \infty$, and if $\left(s_{k_{n}}\right)$ is a subsequence of $\left(s_{n}\right)$, then $\left|s_{k_{n}}\right| \rightarrow \infty$ as $n \rightarrow \infty$.
微积分代考CALCULUS代写|Exponential and Logarithm Functions
For $x \in \mathbb{R}$, the function
$$
\exp (x):=\sum_{n=0}^{\infty} \frac{x^{n}}{n !}, \quad x \in \mathbb{R},
$$
is called the exponential function.
Clearly,
$$
\exp (0)=1, \quad \exp (1)=e .
$$
Our first attempt is to show that
$$
\exp (r)=e^{r}
$$
for every rational number. In order to do that we have to derive some of the important properties of the function $\exp (x)$. For that purpose, we shall make use of the following result on convergence of series.

微积分代考CALCULUS代写|DEFINITION AND SOME BASIC RESULTS
约定:当我们这么说时F在一点上是连续的X0∈R, 我们的意思是F在包含的区间上定义X0和F是连续的X0.
示例 2.2.1 让F(X)=一种0+一种1X+⋯一种到X到对于一些一种0,一种1,…,一种到在R和到∈ñ. 我们知道(参见示例 2.1.8),对于任何X0∈R,
$$
\lim {x \rightarrow x {0}} f(x)=f\left(x_{0}\right) 。
H和nC和,b和吨H和○r和米2.2.1,$F$一世sC○n吨一世n你○你s一种吨和v和r和$X0∈R$(F一世G.2.9).和X一种米p一世和2.2.2一世和吨$F:[−1,1]→R$b和一种s一世n和X一种米p一世和2.1.3,一世.和.,
f(x)=\左{0,−1≤X≤0 1,0<X≤1\正确的。
$$
我们已经看到 $\lim {x \rightarrow 0} f(x)d○和sn○吨和X一世s吨.H和nC和,b和吨H和○r和米2.2.1,F一世sn○吨C○n吨一世n你○你s一种吨0.和X一种米p一世和2.2.3在和H一种v和s和和n一世n和X一种米p一世和s2.1.10一种nd2.1.11吨H一种吨$ \lim {x \rightarrow 0} \sin x=0, \quad \lim {x \rightarrow 0} \cos x=1, \quad \lim {x \rightarrow 0} \frac{\sin x}{x }=1 。
$$
微积分代考CALCULUS代写|SOME MORE EXAMPLES
例 2.2.6 我们已经在例 2.2.3 中观察到函数F,G,H被定义为
F(X)=没有X,G(X)=某物X,H(X)={没有XX,X≠0, 1,X=0
在 0 处连续。现在,我们证明它们在每个点上都是连续的R.
请注意,对于X,和∈R,
没有X−没有和=2没有(X−和2)某物(X+和2)
以便
|没有X−没有和|≤|X−和|∀X,和∈R
因此,对于每个e>0并且对于每个X0∈R,
X∈R,|X−X0|<e⇒|没有X−没有X0|<e.
因此,F在每一点都是连续的R. 自从某物X=1−2没有2(X/2),X∈R, 也随之而来G在每一点都是连续的R. 现在,让X0≠0. 那么连续性H在X0由定理 2.2.6 得出,因为H=F/F0在哪里F0(X)=X在邻域中的非零X0.
微积分代考CALCULUS代写|SOME PROPERTIES OF CONTINUOUS FUNCTIONS
回想一下子集小号的R如果存在则说是有界的米>0这样|s|≤米对所有人s∈小号,无界的集合称为无界集。还记得如果小号是有界子集R, 然后小号有下确界和上确界,不一定在小号.
为了小号⊆R,我们有以下内容:
- 认为小号是有界的,说一种:=信息小号和b:=支持小号. 那么存在序列(sn)和(吨n)在小号这样sn→一种和吨n→b.
- 小号无界当且仅当存在一个序列(sn)在小号这是无界的。
- 小号无界当且仅当存在一个序列(sn)在小号这样|sn|→∞作为n→∞.
- 如果(sn)是一个序列小号无界,则存在子序列(s到n)的(sn)这样|s到n|→∞作为n→∞.
- 如果(sn)是一个序列小号这样|sn|→∞作为n→∞, 而如果(s到n)是一个子序列(sn), 然后|s到n|→∞作为n→∞.
微积分代考CALCULUS代写|EXPONENTIAL AND LOGARITHM FUNCTIONS
为了X∈R, 功能
经验(X):=∑n=0∞Xnn!,X∈R,
称为指数函数。
清楚地,
经验(0)=1,经验(1)=和.
我们的第一个尝试是证明
经验(r)=和r
对于每个有理数。为了做到这一点,我们必须导出函数的一些重要属性经验(X). 为此,我们将利用以下关于级数收敛的结果。

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。