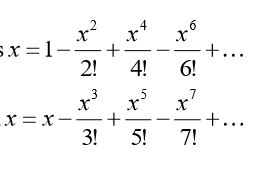You recall the definition of completeness which stated that every nonempty set of real numbers which is bounded above has a least upper bound and that every nonempty set of real numbers which is bounded below has a greatest lower bound and this is a property of the real line known as the completeness axiom. Geometrically, this involved filling in the holes. There is another way of describing completeness in terms of Cauchy sequences. Both of these concepts came during the first part of the nineteenth century and are due to Bolzano and Cauchy.
The next definition has to do with sequences which are real numbers.
68
CHAPTER 4. FUNCTIONS AND SEQUENCES
Definition 4.10.1 The sequence of real numbers, $\left{a_{n}\right}$, is monotone increasing if for all $n, a_{n} \leq a_{n+1}$. The sequence is monotone decreasing if for all $n, a_{n} \geq a_{n+1}$. People often leave off the word “monotone”.
If someone says a sequence is monotone, it usually means monotone increasing.
There exist different descriptions of completeness. An important result is the following theorem which gives a version of completeness in terms of Cauchy sequences. This is often more convenient to use than the earlier definition in terms of least upper bounds and greatest lower bounds because this version of completeness, although it is equivalent to the completeness axiom for the real line, also makes sense in many situations where Definition $2.10 .1$ on Page 26 does not make sense, $C$ for example because by Problem 12 on Page 37 there is no way to place an order on $\mathbb{C}$. This is also the case whenever the sequence is of points in multiple dimensions.
It is the concept of completeness and the notion of limits which sets analysis apart from algebra. You will find that every existence theorem in analysis depends on the assumption that some space is complete. In case of $\mathbb{R}$ the least upper bound version corresponds to a statement about convergence of Cauchy sequences.
Theorem 4.10.2 The following are equivalent.
- Every Cauchy sequence in $\mathbb{R}$ converges
- Every non-empty set of real numbers which is bounded above has a least upper bound.
- Every nonempty set of real numbers which is bounded below has a greatest lower bound.
Proof: $1 . \Rightarrow$ 2. First suppose every Cauchy sequence converges and let $S$ be a nonempty set which is bounded above. Let bi be an upper bound. Pick $s_{1} \in S$. If $s_{1}=b_{1}$, the least upper bound has been found and equals $b_{1}$. If $\left(s_{1}+b_{1}\right) / 2$ is an upper bound to $S$, let this equal $b_{2}$. If not, there exists $b_{1}>s_{2}>\left(s_{1}+b_{1}\right) / 2$ so let $b_{2}=b_{1}$ and $s_{2}$ be as just described. Now let $b_{2}$ and $s_{2}$ play the same role as $s_{1}$ and $b_{1}$ and do the same argument. This yields a sequence $\left{s_{n}\right}$ of points of $S$ which is monotone increasing and another sequence of upper bounds, $\left{b_{n}\right}$ which is monotone decreasing and $\left|s_{n}-b_{n}\right| \leq 2^{-n+1}\left(b_{1}-s_{1}\right) .$ Therefore, if $m>n$
$$
\left|b_{n}-b_{m}\right| \leq b_{n}-s_{m} \leq b_{n}-s_{n} \leq 2^{-n+1}\left(b_{1}-s_{1}\right)
$$
and so $\left{b_{n}\right}$ is a Cauchy sequence. Therefore, it converges to some number $b$. Then $b$ must be an upper bound of $S$ because if not, there would exist $s>b$ and then $b_{n}-b \geq s-b$ which would prevent $\left{b_{n}\right}$ from converging to $b$.
$2
. \Rightarrow 3 ., 3 . \Rightarrow 2$. The claim that every non
empty set of numbers bounded below has a greatest lower bou
nd follows similarly. Alternatively, you could consider $-S \equiv$ $
{-x: x \in S}$ and apply what was just shown. If $S$ is boundod b
elow, then $-S$ is bounded above and so there exists a least uppe
r bound for $-S$ called $-l$. Then $l$ is a lower bound to $S$. If t
here is $b>l$ such that $b$ is also a lower bound to $S$, then $-
$
$b_{n}-b \geq s-b$ which would prevent $\left{b_{n}\right}$ from converging to $b$.
$2 . \Rightarrow 3 ., 3 . \Rightarrow 2$. The claim that every nonempty set of numbers bounded below has a greatest lower bound follows similarly. Alternatively, you could consider $-S \equiv$ ${-x: x \in S}$ and apply what was just shown. If $S$ is bounded below, then $-S$ is bounded above and so there exists a least upper bound for $-S$ called $-l$. Then $l$ is a lower bound to $S$. If there is $b>l$ such that $b$ is also a lower bound to $S$, then $-b$ would also be an upper bound to $-S$ and would be smaller than $-l$ which contradicts the definition of $-l$. Hence $l$ is the greatest lower bound to $S$. To show $3 . \Rightarrow 2 .$, also consider $-S$ and apply 3 . to it similar to what was just done in showing $2 . \Rightarrow 3$.
$2.3 . \Rightarrow 1$.Now suppose the condition sbout existence of least upper bounds and greatest lower bounds. Let $\left{a_{n}\right}$ be a Cauchy sequence. Then by Theorem $4.5 .2\left{a_{n}\right} \subseteq$ $[a, b]$ for some numbers $a, b$. By Theorem $4.8 .2$ there is a subsequence, $\left{a_{n_{k}}\right}$ which converges to $x \in[a, b]$. By Theorem 4.5.4 the original sequence converges to $x$ also.
Theorem 4.10.3 If either of the above conditions for completeness holds, then whenever $\left{a_{n}\right}$ is a monotone increasing sequence which is bounded above, it converges and whenever $\left{b_{n}\right}$ is a monotone sequence which is bounded below, it converges.
4.10. CAUCHY SEQUENCES AND COMPLETENESS
69
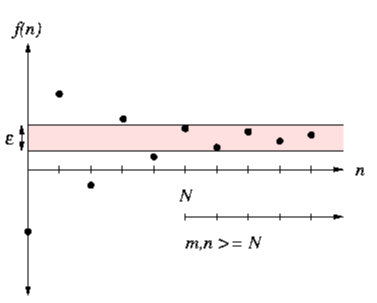
Proof: Let $a=\sup \left{a_{n}: n \geq 1\right}$ and let $\varepsilon>0$ be given. Then from Proposition $2.10 .3$ on Page 26 there exists $m$ such that $a-\varepsilon<a_{r n} \leq a$. Since the sequence is increasing, it follows that for all $n \geq m, a-\varepsilon<a_{n} \leq a$. Thus $a=\lim {n \rightarrow \infty} a{n-}$.The case of a decreasing sequence is similar. Alternatively, you could consider the sequence $\left{-a_{n}\right}$ and apply what was just shown to this decreasing sequence.
By Theorem $4.10 .2$ the following definition of completeness is equivalent to the original definition when both apply. However, note that convergence of Cauchy sequences does not depend on an order to it applies to much more general situations. Recall from Theorem $4.8 .13$ that $\mathbb{C}$ and $\mathbb{F}$ are complete. Just apply that theorem to the case where $p=1$.
微积分note Cauchy Sequences and Completeness
您还记得完整性的定义,该定义指出,上界的每个非空实数集都有一个最小上界,而下界的每个非空实数集都有一个最大下界,这是实线的属性称为完备性公理。在几何上,这涉及填充孔。还有另一种用柯西序列来描述完整性的方法。这两个概念都是在 19 世纪上半叶出现的,归功于博尔扎诺和柯西。
下一个定义与实数序列有关。
68
第 4 章函数和序列
定义 4.10.1 实数序列 $\left{a_{n}\right}$ 是单调递增的,如果对于所有 $n,a_{n} \leq a_{n+1}$。如果对于所有 $n,a_{n} \geq a_{n+1}$,该序列是单调递减的。人们经常忽略“单调”这个词。
如果有人说一个序列是单调的,那通常意味着单调递增。
对完整性有不同的描述。一个重要的结果是以下定理,它给出了柯西序列的完整性版本。就最小上界和最大下界而言,这通常比先前的定义更方便使用,因为这个版本的完整性虽然等同于实线的完整性公理,但在定义 $2.10 的许多情况下也是有意义的。第 26 页的 1$ 没有意义,例如 $C$,因为第 37 页的问题 12 没有办法在 $\mathbb{C}$ 上下订单。每当序列是多维点时,情况也是如此。
正是完整性概念和极限概念将分析与代数区分开来。你会发现分析中的每一个存在定理都依赖于某个空间是完备的假设。在 $\mathbb{R}$ 的情况下,最小上界版本对应于关于柯西序列收敛的陈述。
定理 4.10.2 以下是等价的。
- $\mathbb{R}$ 中的每个柯西序列都收敛
- 上界的每一个非空实数集都有一个最小上界。
- 每一个有界的非空实数集都有一个最大的下界。
证明:1美元。 \Rightarrow$ 2. 首先假设每个柯西序列收敛并且令$S$ 是一个有界的非空集。设 bi 为上限。选择 $s_{1} \in S$。如果 $s_{1}=b_{1}$,则已找到最小上限并等于 $b_{1}$。如果 $\left(s_{1}+b_{1}\right) / 2$ 是 $S$ 的上限,则令其等于 $b_{2}$。如果不存在,则存在 $b_{1}>s_{2}>\left(s_{1}+b_{1}\right) / 2$ 所以令 $b_{2}=b_{1}$ 和 $s_ {2}$ 如前所述。现在让 $b_{2}$ 和 $s_{2}$ 扮演与 $s_{1}$ 和 $b_{1}$ 相同的角色并执行相同的参数。这产生一个序列 $\left{s_{n}\right}$ 单调递增的 $S$ 点和另一个上界序列 $\left{b_{n}\right}$是单调递减且 $\left|s_{n}-b_{n}\right| \leq 2^{-n+1}\left(b_{1}-s_{1}\right) .$ 因此,如果 $m>n$
$$
\left|b_{n}-b_{m}\right| \leq b_{n}-s_{m} \leq b_{n}-s_{n} \leq 2^{-n+1}\left(b_{1}-s_{1}\right)
$$
所以 $\left{b_{n}\right}$ 是一个柯西序列。因此,它收敛到某个数 $b$。然后 $b$ 必须是 $S$ 的上限,因为如果不是,则存在 $s>b$ 然后 $b_{n}-b \geq sb$ 这将阻止 $\left{b_{n} \right}$ 从收敛到 $b$。
2美元
. \右箭头 3 ., 3 . \右箭头 2$。声称每个非
下面有界的空数字集具有最大的下边界
nd 类似。或者,您可以考虑 $-S \equiv$ $
{-x: x \in S}$ 并应用刚刚显示的内容。如果 $S$ 是绑定 b
elow,那么 $-S$ 是有界的,所以存在一个最小的 uppe
r 绑定到 $-S$ 称为 $-l$。那么$l$ 是$S$ 的下界。如果
这里是 $b>l$ 使得 $b$ 也是 $S$ 的下限,然后是 $-
$
$b_{n}-b \geq s-b$ 这将阻止 $\left{b_{n}\right}$ 收敛到 $b$。
2 美元。 \右箭头 3 ., 3 . \右箭头 2$。下界的每一个非空数集都有一个最大的下界的主张类似地遵循。或者,您可以考虑 $-S \equiv$ ${-x: x \in S}$ 并应用刚刚显示的内容。如果 $S$ 的下界,则 $-S$ 的上界,因此存在 $-S$ 的最小上界,称为 $-l$。那么$l$ 是$S$ 的下界。如果存在 $b>l$ 使得 $b$ 也是 $S$ 的下限,那么 $-b$ 也将是 $-S$ 的上限并且小于 $-l$,这与$-l$ 的定义。因此,$l$ 是 $S$ 的最大下限。显示 $3 。 \Rightarrow 2 .$,也考虑 $-S$ 并应用 3 。它类似于刚刚在显示 $2 时所做的。 \右箭头 3$。
2.3 美元。 \Rightarrow 1$。现在假设条件 sbout 存在最小上界和最大下界。令 $\left{a_{n}\right}$ 为柯西序列。然后通过定理 $4.5 .2\left{a_{n}\right} \subseteq$ $[a, b]$ 对于一些数字 $a

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。