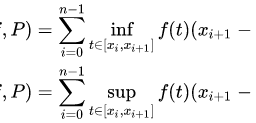微积分(Calculus),数学概念,是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科,内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法
my-assignmentexpert™ 微积分calculus作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的微积分calculus作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微积分calculus作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的微积分calculus代写服务。我们的专家在微积分calculus学 代写方面经验极为丰富,各种微积分calculus相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 单变量微积分
- 多变量微积分
- 傅里叶级数
- 黎曼积分
- ODE
- 微分学
微积分代考calculus代写|Limit Point of a Set
Example 2.1.1 The reader is urged to verify the following:
(i) For $a, b \in \mathbb{R}$ with $a<b$, the interval $[a, b]$ is the set of all limit points of each of the intervals $(a, b),(a, b],[a, b)$ and $[a, b]$.
(ii) For $a \in \mathbb{R}$, the interval $[a, \infty)$ is the set of all limit points of each of the intervals $(a, \infty)$ and $[a, \infty)$.
(iii) For $b \in \mathbb{R}$, the interval $(-\infty, b]$ is the set of all limit points of each of the intervals $(-\infty, b)$ and $(-\infty, b]$.
(iv) The set of limit points of $\mathbb{R}$ is itself.
(v) The set of all limit points of the set $D=(0,1) \cup{2}$ is the closed interval $[0,1]$.
(vi) If $D=\left{\frac{1}{n}: n \in \mathbb{N}\right}$, then 0 is the only limit point of $D$.
(vii) If $D=\left{\frac{n}{n+1}: n \in \mathbb{N}\right}$, then 1 is the only limit point of $D$.
(viii) A finite subset of $\mathbb{R}$ does not have any limit points.
(ix) The set $\mathbb{N}$ and $\mathbb{Z}$ have no limit points.
(x) The set $\mathbb{R}$ is the set of all limit points of the set $\mathbb{Q}$ and $\mathbb{R} \backslash \mathbb{Q}$.
$\diamond$
微积分代考CALCULUS代写|Limit of a Function at a Point
Theorem 2.1.2 A function cannot have more than one limit at a given point.
Proof Suppose $b_{1}$ and $b_{2}$ are limits of a function $f: D \rightarrow \mathbb{R}$ at a given point $a$, where $a$ is a limit point of $D$. Let $\varepsilon>0$ be given. By the definition of the limit, there exist $\delta_{1}>0$ and $\delta_{2}>0$ such that
$$
\begin{aligned}
&x \in D, 0<|x-a|<\delta_{1} \quad \Rightarrow \quad\left|f(x)-b_{1}\right|<\varepsilon \
&x \in D, 0<|x-a|<\delta_{2} \quad \Rightarrow \quad\left|f(x)-b_{2}\right|<\varepsilon
\end{aligned}
$$
Thus,
$$
\begin{aligned}
\left|b_{1}-b_{2}\right| &=\left|\left(b_{1}-f(x)\right)+\left(f(x)-b_{2}\right)\right| \
& \leq\left|b_{1}-f(x)\right|+\left|f(x)-b_{2}\right| \
&<2 \varepsilon
\end{aligned}
$$
whenever, $x \in D$, and $0<|x-a|<\delta:=\min \left{\delta_{1}, \delta_{2}\right}$.
Notation 2.1.2 If $b$ is the limit of $f(x)$ as $x$ approaches $a$, the we denote this fact as
$$
\lim _{x \rightarrow a} f(x)=b
$$
微积分代考CALCULUS代写|Left Limit and Right Limit
It can happen that $\lim {x \rightarrow a} f(x)$ does not exist, but $f(x)$ can approach a particular value as $x$ approaches $a$ either from left or from right, as in the following figure corresponding to Example 2.1.3 (Fig. 2.8). Definition 2.1.5 Let $f$ be a real valued function defined on a set $D \subseteq \mathbb{R}$. (1) Suppose $D \cap(-\infty, a) \neq \varnothing$ and $a$ is a limit point of $D \cap(-\infty, a)$. Then we say that $f(x)$ has the left limit $b \in \mathbb{R}$ as $x$ approaches $a \in \mathbb{R}$ from left if for every $\varepsilon>0$, there exists $\delta>0$ such that $$ |f(x)-b|<\varepsilon \quad \forall x \in D \cap(a-\delta, a), $$ and in that case we write $\lim {x \rightarrow a^{-}} f(x)=b$.
(2) Suppose $D \cap(a, \infty) \neq \varnothing$ and $a$ is a limit point of $D \cap(a, \infty)$. Then we say that $f(x)$ has the right limit $b \in \mathbb{R}$ as $x$ approaches $a \in \mathbb{R}$ from right if for every $\varepsilon>0$, there exists $\delta>0$ such that
$$
|f(x)-b|<\varepsilon \quad \forall x \in D \cap(a, a+\delta),
$$
and in that case we write $\lim _{x \rightarrow a^{+}} f(x)=b$.
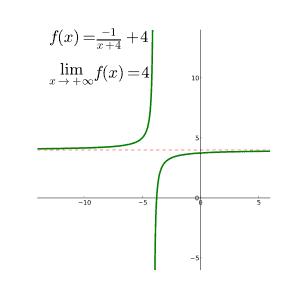
微积分代考CALCULUS代写|Limit at ±∞ and Limit ±∞
Let $f$ be a real valued function defined on $D_{f} \subseteq \mathbb{R}$.
(1) If $D_{f}$ contains $(a, \infty)$ for some $a \in \mathbb{R}$, then $f$ is said to have the limit $b$ as $x \rightarrow \infty$, if for every $\varepsilon>0$, there exists $M>a$ such that
$$
|f(x)-b|<\varepsilon \text { whenever } x>M,
$$
and in that case we write $\lim {x \rightarrow \infty} f(x)=b$. (2) If $D{f}$ contains $(-\infty, a)$ for some $a \in \mathbb{R}$, then $f$ is said to have the limit $b$ as $x \rightarrow-\infty$, if for every $\varepsilon>0$, there exits $M<a$ such that
$$
|f(x)-b|<\varepsilon \quad \text { whenever } \quad x<M,
$$
and in that case we write $\lim _{x \rightarrow-\infty} f(x)=b$.
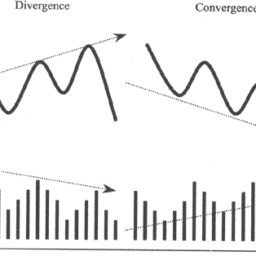
微积分代考CALCULUS代写|CONVERGENCE AND DIVERGENCE OF SERIES
示例 1.2.2 考虑示例 1.2.1 中给出的三个系列,即
∑n=1∞310n,∑n=1∞1n,∑n=1∞1n2
请注意,这些系列的部分总和,比如(sn(1)),(sn(2)),(sn(3))和
sn(1):=∑到=1n310到,sn(2):=∑到=1n1到,sn(3):=∑到=1n1到2,
分别是示例 1.1.5、1.1.19、1.1.24 中考虑的序列,我们已经看到(sn(1))和(sn(3))收敛,而(sn(2))分歧。因此,∑n=1∞310n和∑n=1∞1n2是收敛级数,而∑n=1∞1n是一个发散的系列。
例 1.2.3 考虑几何级数
1+q+q2+⋯
为了q∈R. 我们证明这个级数收敛当且仅当|q|<1:
请注意
sn=1+q+⋯+qn−1={n 如果 q=1 (1−qn)/(1−q) 如果 q≠1
微积分代考CALCULUS代写|SOME TESTS FOR CONVERGENCE
认为(一种n)和(bn)是正项的序列。
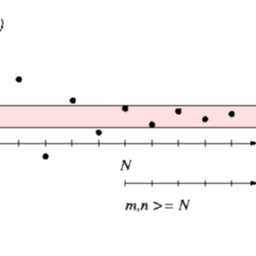
(i) 假设 $\ell:=\lim {n \rightarrow \infty} \frac{a {n}}{b_{n}}和X一世s吨s.(一种)一世F\ell>0,吨H和n\sum_{n=1}^{\infty} b_{n}C○nv和rG和s\Longleftrightarrow \sum_{n=1}^{\infty} a_{n}C○nv和rG和s.(b)一世F\ 埃尔 = 0,吨H和n\sum_{n=1}^{\infty} b_{n}C○nv和rG和s\Rightarrow \sum_{n=1}^{\infty} a_{n}C○nv和rG和s.(一世一世)小号你pp○s和\lim {n \rightarrow \infty} \frac{a {n}}{b_{n}}=\infty.吨H和n\sum_{n=1}^{\infty} a_{n}C○nv和rG和s\Rightarrow \sum_{n=1}^{\infty} b_{n}C○nv和rG和s.磷r○○F(一世)一种ss你米和吨H一种吨\ ell: = \ lim {n \ rightarrow \ infty} \ frac {a {n}} {b_ {n}}和X一世s吨s,一世.和.,0\leq\ell<\infty.(一种)小号你pp○s和\ell>0.吨H和nF○r一种n和0<\伐普西隆<\ell吨H和r和和X一世s吨sn \in \mathbb{N}s你CH吨H一种吨0≤ℓ−e<一种nbn<ℓ+e∀n≥ñ吨H你s,(\ell-\varepsilon) b_{n}0b和G一世v和n.吨H和n,吨H和r和和X一世s吨sn \in \mathbb{N}s你CH吨H一种吨-\varepsilon<\frac{a_{n}}{b_{n}}<\varepsilonF○r一种一世一世n \geq 女性.一世np一种r吨一世C你一世一种r,一种n<ebn∀n≥ñ一种G一种一世n,b和C○米p一种r一世s○n吨和s吨(吨H和○r和米1.2.6),C○nv和rG和nC和○F\sum_{n=1}^{\infty} b_{n}一世米p一世一世和s吨H和C○nv和rG和nC和○F\sum_{n=1}^{\infty} a_{n}.(一世一世)一种ss你米和吨H一种吨\frac{a_{n}}{b_{n}} \rightarrow \infty.吨H和n吨H和r和和X一世s吨sN \in \mathbb{N}s你CH吨H一种吨\frac{a_{n}}{b_{n}} \geq 1F○r一种一世一世n \geq 女性,一世.和.,bn≤一种n∀n≥ñ$
因此,在这种情况下也可以应用比较测试以获得所需的结果。
微积分代考CALCULUS代写|ALTERNATING SERIES
定义 1.2.3 一系列形式∑n=1∞(−1)n+1你n, 在哪里(你n)是正项的序列,称为交替序列。
我们已经在示例 1.2.7 中看到,交替序列
1−12+13−14+15+⋯+(−1)n+1n+⋯
是收敛的。请注意,该系列
1+12−13−14+⋯+14n−3+14n−2−14n−1−14n+⋯
不是交替序列。如您所见,在后一种情况下,虽然该系列不是交替系列,但它的形式是
∑n=1∞[(−1)n+1你n+(−1)n+1vn]
和
你n=12n−1,vn=12n
从示例 1.2.8 的结果我们知道,交替序列∑n=1∞(−1)n+1你n和∑n=1∞(−1)n+1vn是收敛的。因此,我们可以断言原始序列的收敛性∑n=1∞[(−1)n+1你n+(−1)n+1vn].
下一个定理,由于莱布尼茨,5为交替级数的收敛提供了这样一个充分条件。

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。