如果你也在 怎样统计计算Statistical Computing这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。统计计算Statistical Computing是统计学和计算机科学之间的纽带。它意味着通过使用计算方法来实现的统计方法。它是统计学的数学科学所特有的计算科学(或科学计算)的领域。这一领域也在迅速发展,导致人们呼吁应将更广泛的计算概念作为普通统计教育的一部分。与传统统计学一样,其目标是将原始数据转化为知识,[2]但重点在于计算机密集型统计方法,例如具有非常大的样本量和非同质数据集的情况。
许多统计建模和数据分析技术可能难以掌握和应用,因此往往需要使用计算机软件来帮助实施大型数据集并获得有用的结果。S-Plus是公认的最强大和最灵活的统计软件包之一,它使用户能够应用许多统计方法,从简单的回归到时间序列或多变量分析。该文本广泛涵盖了许多基本的和更高级的统计方法,集中于图形检查,并具有逐步说明的特点,以帮助非统计学家充分理解方法。
my-assignmentexpert™统计计算Statistical Computing作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的统计计算Statistical Computing作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此统计计算Statistical Computing作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在统计计算Statistical Computing作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计计算Statistical Computing代写服务。我们的专家在统计计算Statistical Computing代写方面经验极为丰富,各种统计计算Statistical Computing相关的作业也就用不着 说。
我们提供的统计计算Statistical Computing及其相关学科的代写,服务范围广, 其中包括但不限于:
- 随机微积分 Stochastic calculus
- 随机分析 Stochastic analysis
- 随机控制理论 Stochastic control theory
- 微观经济学 Microeconomics
- 数量经济学 Quantitative Economics
- 宏观经济学 Macroeconomics
- 经济统计学 Economic Statistics
- 经济学理论 Economic Theory
- 计量经济学 Econometrics
统计代写
数学代写|统计计算作业代写Statistical Computing代考|Abstract Modeling fatigue life
Abstract Modeling fatigue life is complex whether it is applied to structures or experimental programs. Through the years several empirical approaches have been utilized. Each approach has positive aspects; however, none have been acceptable for every circumstance. On many occasions the primary shortcoming for an empirical method is the lack of a sufficiently robust database for statistical modeling. The modeling is exacerbated for loading near typical operating conditions because the scatter in the fatigue lives is quite large. The scatter may be attributed to microstructure, manufacturing, or experimental inconsistencies, or a combination thereof. Empirical modeling is more challenging for extreme life estimation because those events are rare. The primary purpose herein is to propose an empirically based methodology for estimating the cumulative distribution functions for fatigue life, given the applied load. The methodology incorporates available fatigue life data for various stresses or strains using a statistical transformation to merge all the life data so that distribution estimation is more accurate than traditional approaches. Subsequently, the distribution for the transformed and merged data is converted using change-of-variables to estimate the distribution for each applied load. To assess the validity of the proposed methodology percentile bounds are estimated for the life data. The development of the methodology and its subsequent validation is illustrated using three sets of fatigue life data which are readily available in the open literature.
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|Fatigue Life Data
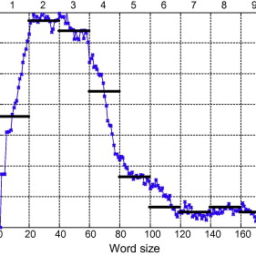
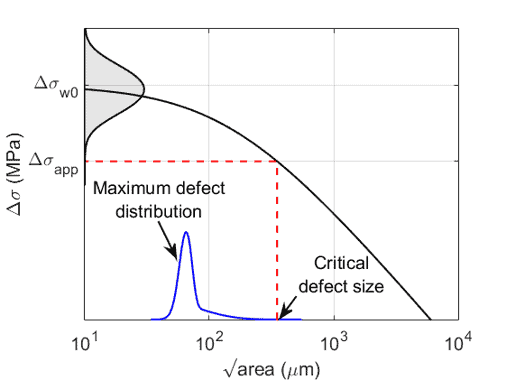
Fatigue life data are most often presented on an S-N plot which shows the fatigue data for a given load. The load is typically stress or strain. Thus $S-N$ can represent stress-life or strain-life. An additional way in which the fatigue data are presented is on a probability plot. Both of these representations will be used subsequently. Three different sets of fatigue life data are considered for the proposed method.
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|Data Fusion for Fatigue Life Analysis
The choices of $a$ and $b$ in Eq. (1) are easily determined by simple algebra to be the following:
$$
a=\frac{s_{A}}{s_{y}} \text { and } b=N_{A}-\frac{s_{A}}{s_{y}} \bar{y},
$$
where $\bar{y}$ is the average and $s_{y}$ is the sample standard deviation for $\left{y_{j}: 1 \leq j \leq n\right}$, and $N_{A}$ and $s_{A}$ are arbitrary values chosen for normalization.
For fatigue data the life times are distributed over several orders of magnitude that the procedure in Eqs. (1) and (2) is applied to the natural logarithm of the life times. Let $m$ be the number of different values of applied stress or strain, i.e., $\left{\Delta \sigma_{k}: 1 \leq k \leq m\right}$ or $\left{\Delta \varepsilon_{k}: 1 \leq k \leq m\right}$. Given $\Delta \sigma_{k}$ or $\Delta \varepsilon_{k}$ the associated life times are $\left{N_{k, j}: 1 \leq j \leq n_{k}\right}$ where $n_{k}$ is its sample size. Let
$$
y_{k, j}=\ln \left(N_{k, j}\right)
$$
be the transformed life times. Substituting Eq. (2) into Eq. (1) leads to the following:
$$
z_{k, j}=\frac{s_{A}}{s_{y, k}}\left(y_{k, j}-\bar{y}{k}\right)+N{A} .
$$
Thus, the averages and sample standard deviations of $\left{y_{k, j}: 1 \leq j \leq n_{k}\right}$ and $\left{z_{k, j}: 1 \leq j \leq n_{k}\right}$ are equal to each other. The next step is to merge all the transformed $z_{k, j}$ values from Eq. (4) for $1 \leq j \leq n_{k}$ and $1 \leq k \leq m$. The purpose in using the merged values is to have a more extensive dataset for estimation of the cdf. This is especially critical for estimating the extremes of the cdf more accurately. Subsequently, an appropriate cdf $F_{Z}(z)$ is found that characterizes the merged data. It is assumed that this cdf also characterizes the subsets $\left{z_{k, j}: 1 \leq j \leq n_{k}\right}$ of the merged set. With this assumption and the linear transformation in Eq. (4), the cdfs for $\left{y_{k, j}: 1 \leq j \leq n_{k}\right} F_{y, k}(y)$ can be derived from $F_{Z}(z)$ as follows:
$$
F_{y, k}(y)=F_{Z}\left(\frac{s_{A}}{s_{y, k}}\left(y-\bar{y}{k}\right)+N{A}\right) .
$$
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|ABSTRACT MODELING FATIGUE LIFE
摘要 疲劳寿命建模无论是应用于结构还是实验程序都是复杂的。多年来,已经使用了几种经验方法。每种方法都有积极的方面;然而,没有一个在任何情况下都是可以接受的。在许多情况下,经验方法的主要缺点是缺乏用于统计建模的足够健壮的数据库。由于疲劳寿命的分散非常大,因此在典型操作条件附近加载时会加剧建模。分散可归因于微观结构、制造或实验不一致或其组合。经验建模对于极端寿命估计更具挑战性,因为这些事件很少见。本文的主要目的是提出一种基于经验的方法,用于在给定施加载荷的情况下估计疲劳寿命的累积分布函数。该方法使用统计转换合并所有寿命数据,从而结合各种应力或应变的可用疲劳寿命数据,从而使分布估计比传统方法更准确。随后,转换和合并数据的分布使用变量变化进行转换,以估计每个应用负载的分布。为了评估所提出的方法的有效性,对寿命数据进行百分位界限的估计。使用公开文献中容易获得的三组疲劳寿命数据来说明该方法的开发及其随后的验证。
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|FATIGUE LIFE DATA
疲劳寿命数据最常显示在 SN 图上,该图显示了给定负载的疲劳数据。负载通常是应力或应变。因此小号−ñ可以表示应力寿命或应变寿命。呈现疲劳数据的另一种方式是在概率图上。随后将使用这两种表示形式。所提出的方法考虑了三组不同的疲劳寿命数据。
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|DATA FUSION FOR FATIGUE LIFE ANALYSIS
的选择一种和b在等式。1很容易通过简单代数确定如下:
一种=s一种s和 和 b=ñ一种−s一种s和和¯,
在哪里和¯是平均值并且s和是样本标准差\left{y_{j}: 1 \leq j \leq n\right}\left{y_{j}: 1 \leq j \leq n\right}, 和ñ一种和s一种是为标准化选择的任意值。
对于疲劳数据,寿命分布在方程式中的程序的几个数量级上。1和2应用于寿命的自然对数。让米是施加的应力或应变的不同值的数量,即\left{\Delta \sigma_{k}: 1 \leq k \leq m\right}\left{\Delta \sigma_{k}: 1 \leq k \leq m\right}要么\left{\Delta\varepsilon_{k}:1\leq k\leq m\right}\left{\Delta\varepsilon_{k}:1\leq k\leq m\right}. 给定Δσ到要么Δe到相关的寿命是\left{N_{k, j}: 1 \leq j \leq n_{k}\right}\left{N_{k, j}: 1 \leq j \leq n_{k}\right}在哪里n到是它的样本量。让
和到,j=ln(ñ到,j)
成为改变的生命时代。代入方程式。2进入方程。1导致以下结果:
$$
z_{k, j}=\frac{s_{A}}{s_{y, k}}\left(y_{k, j}-\bar{y} {k}\right )+N {A} 。
因此,$\left{y_{k, j} 的平均值和样本标准差: 1 \leq j \leq n_{k}\right}$ 和 $\left{z_{k, j}: 1 \leq j \leq n_{k}\right}$ 彼此相等。下一步是合并来自方程式的所有转换后的 $z_{k, j}$ 值。(4) 对于 $1 \leq j \leq n_{k}$ 和 $1 \leq k \leq m$。使用合并值的目的是获得更广泛的数据集来估计 cdf。这对于更准确地估计 cdf 的极值尤其重要。随后,找到一个合适的 cdf $F_{Z}(z)$ 来表征合并的数据。假设这个 cdf 也表征了合并集的子集 $\left{z_{k, j}: 1 \leq j \leq n_{k}\right}$。有了这个假设和方程式中的线性变换。(4)、$\left{y_{k, j} 的 cdfs: 1 \leq j \leq n_{k}\right} F_{y,Thus, the averages and sample standard deviations of $\left{y_{k, j}: 1 \leq j \leq n_{k}\right}$ and $\left{z_{k, j}: 1 \leq j \leq n_{k}\right}$ are equal to each other. The next step is to merge all the transformed $z_{k, j}$ values from Eq. (4) for $1 \leq j \leq n_{k}$ and $1 \leq k \leq m$. The purpose in using the merged values is to have a more extensive dataset for estimation of the cdf. This is especially critical for estimating the extremes of the cdf more accurately. Subsequently, an appropriate cdf $F_{Z}(z)$ is found that characterizes the merged data. It is assumed that this cdf also characterizes the subsets $\left{z_{k, j}: 1 \leq j \leq n_{k}\right}$ of the merged set. With this assumption and the linear transformation in Eq. (4), the cdfs for $\left{y_{k, j}: 1 \leq j \leq n_{k}\right} F_{y, k}(y)$ can be derived from $F_{Z}(z)$ as follows:
F_{y, k}和=F_{Z}\left(\frac{s_{A}}{s_{y, k}}\left(y-\bar{y} {k}\right)+N {A}\right) 。
$$

计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写