数学代写|复分析代写complex analysis代考|The geometric interpretation of the derivative

如果你也在 怎样代写复分析complex analysis这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。复分析complex analysis传统上称为复变函数理论，是数学分析的一个分支，研究复数函数。它对数学的许多分支都有帮助，包括代数几何、数论、分析组合学、应用数学；以及物理学。数论、分析组合学、应用数学；以及物理学，包括流体力学、热力学，特别是量子力学等分支。推而广之，复数分析在工程领域也有应用，如核、航天、机械和电气工程。

复分析complex analysis复数分析的核心工具之一是线积分。正如Cauchy积分定理所指出的那样，在封闭路径所包围的区域内到处都是全形函数，其围绕封闭路径的线积分总是为零。这样一个全形函数在圆盘内的数值可以通过圆盘边界上的路径积分来计算（如考奇积分公式所示）。复平面内的路径积分经常被用来确定复杂的实积分，这里适用于残差理论等（。一个函数的 “极点”（或孤立的奇点）是指该函数的值变得无界，或 “爆炸 “的一个点。如果一个函数有这样一个极点，那么人们可以在那里计算函数的残差，这可以用来计算涉及该函数的路径积分；这就是强大的残差定理的内容。

my-assignmentexpert™ 复分析complex analysis作业代写，免费提交作业要求， 满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕 博写手团队，所有订单可靠准时，保证 100% 原创。my-assignmentexpert™， 最高质量的复分析complex analysis作业代写，服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。 由于统计Statistics作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此复分析complex analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的复分析complex analysis代写服务。我们的专家在数学mathematics代写方面经验极为丰富，各种复分析complex analysis相关的作业也就用不着 说。

我们提供的复分析complex analysis及其相关学科的代写，服务范围广, 其中包括但不限于:

数学代写|复分析代写complex analysis代考|the starting point

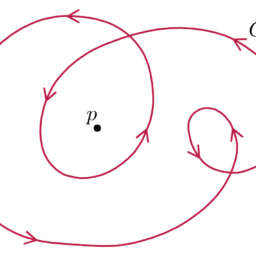
The point $\gamma(0)$ is called the starting point, while the point $\gamma(1)$ is called the end point of the path $\gamma$.
Definition 2.4.2.

1. The set ${y}=\gamma([0,1])$ is called the image of the path $\gamma$.
2. The paths $y_{1}$ and $y_{2}$ are called equivalent paths, denoted by $\gamma_{1} \sim y_{2}$, if $\exists h:[0,1] \rightarrow$ $[0,1]$ a continuous bijection, with $h^{-1}$ continuous, and $h(0)=0, h(1)=1$, such that $y_{1}=y_{2} \circ h$.
3. If $y \in C^{1}[0,1]$, with $\gamma^{\prime}(t) \neq 0, \forall t \in[0,1]$, then $\gamma$ is called a smooth path.
   Remarks 2.4.1.
4. If $y \in C^{1}[0,1]$, with $\gamma^{\prime}\left(t_{0}\right)=\alpha^{\prime}\left(t_{0}\right)+i \beta^{\prime}\left(t_{0}\right) \neq 0$, then $\alpha^{\prime}\left(t_{0}\right)$ and $\beta^{\prime}\left(t_{0}\right)$ are called the directional parameters of the tangent to the path ${y}$ into the point $\gamma\left(t_{0}\right)$.
5. If ${y}$ is a smooth path, then there exists a tangent to it in every point on ${y}$. If $\theta$ is the angle between the $O x$ axis and this tangent, then
   $$
   \theta=\arg \gamma^{\prime}\left(t_{0}\right)=\arctan \frac{\beta^{\prime}\left(t_{0}\right)}{\alpha^{\prime}\left(t_{0}\right)}
   $$
6. If $y_{1}$ and $y_{2}$ are two smooth paths, with $\gamma_{1}\left(t_{0}\right)=y_{2}\left(t_{0}\right)=z_{0}$, then the angle between $\gamma_{1}$ and $\gamma_{2}$ at the point $z_{0}$ is the angle between the tangents to both of these paths into the point $z_{0}$.

数学代写|复分析代写COMPLEX ANALYSIS代考|firstorder conformal map at the point

Definition 2.4.3.

1. Let $G \subset \mathbb{C}$ be an open set and let $f \in C^{1}(G)$. The function $f$ is said to be a firstorder conformal map at the point $z_{0} \in G$, if the angle at $z_{0} \in G$ between any arbitrary smooth paths $\gamma_{1}$ and $\gamma_{2}$, that start from $z_{0}$, is the same with the angle at $f\left(z_{0}\right)$ between their images $f \circ y_{1}$ and $f \circ y_{2}$.
2. The function $f$ is called direct conformal mapping or inverse conformal mapping, if the directions of the angles is preserved, or respectively is changed.
3. The function $f$ is said to be a second-order conformal map at the point $z_{0} \in G$, if the length of any rectifiable smooth path that starts from $z_{0}=\gamma(0)$ is modified “in the same way” by the function $f$, i. e.,
   $$
   \left|(f \circ y)^{\prime}(0)\right|=k\left|y^{\prime}(0)\right|, \quad \forall y \text { smooth path, } y(0)=z_{0}
   $$
   and the constant $k$ is independent of $y$ and it is called the linear deformation (distortion) coefficient of the function $f$ into the point $z_{0}$.

复分析代写

数学代写|复分析代写COMPLEX ANALYSIS代考|THE STARTING POINT

重点C(0)称为起点，而点C(1)被称为路径的终点C.
定义 2.4.2。

1. 套装是=C([0,1])被称为路径的图像C.
2. 路径是1和是2被称为等价路径，记为C1∼是2， 如果∃H:[0,1]→ [0,1]连续双射，有H−1连续的，并且H(0)=0,H(1)=1, 这样是1=是2∘H.
3. 如果是∈C1[0,1]， 和C′(吨)≠0,∀吨∈[0,1]， 然后C称为平滑路径。
   备注 2.4.1。
4. 如果是∈C1[0,1]， 和C′(吨0)=一种′(吨0)+一世b′(吨0)≠0， 然后一种′(吨0)和b′(吨0)称为路径切线的方向参数是切入点C(吨0).
5. 如果是是一条光滑的路径，那么在它的每一点上都有一条切线是. 如果θ是之间的角度这X轴和这个切线，然后
   θ=生气的⁡C′(吨0)=反正切⁡b′(吨0)一种′(吨0)
6. 如果是1和是2是两条平滑的路径，其中C1(吨0)=是2(吨0)=和0，然后之间的角度C1和C2在这一点上和0是这两条路径的切线之间的角度和0.

数学代写|复分析代写COMPLEX ANALYSIS代考|FIRSTORDER CONFORMAL MAP AT THE POINT

定义 2.4.3。

1. 让G⊂C是一个开集并且让F∈C1(G). 功能F据说是该点的一阶保角映射和0∈G, 如果角度在和0∈G在任意平滑路径之间C1和C2，从和0, 与角度相同F(和0)在他们的图像之间F∘是1和F∘是2.
2. 功能F如果角度的方向保持不变或分别改变，则称为直接保形映射或逆保形映射。
3. 功能F据说是该点的二阶保形映射和0∈G, 如果任何可修正的平滑路径的长度从和0=C(0)被函数“以同样的方式”修改F， IE，
   |(F∘是)′(0)|=到|是′(0)|,∀是 平坦的道路， 是(0)=和0
   和常数到独立于是它被称为线性变形d一世s吨这r吨一世这n函数系数F切入点和0.

数学代写|复分析代写complex analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

怎么学好数论

图论代写

数论代写

算法代写

随机多项式代写

抽象代数代写