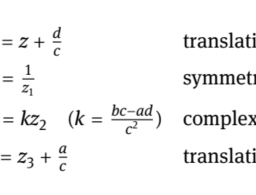数学代写|复分析代写complex analysis代考|The index of a path (curve) with respect to a point

如果你也在 怎样代写复分析complex analysis这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。复分析complex analysis传统上称为复变函数理论，是数学分析的一个分支，研究复数函数。它对数学的许多分支都有帮助，包括代数几何、数论、分析组合学、应用数学；以及物理学。数论、分析组合学、应用数学；以及物理学，包括流体力学、热力学，特别是量子力学等分支。推而广之，复数分析在工程领域也有应用，如核、航天、机械和电气工程。

复分析complex analysis复数分析的核心工具之一是线积分。正如Cauchy积分定理所指出的那样，在封闭路径所包围的区域内到处都是全形函数，其围绕封闭路径的线积分总是为零。这样一个全形函数在圆盘内的数值可以通过圆盘边界上的路径积分来计算（如考奇积分公式所示）。复平面内的路径积分经常被用来确定复杂的实积分，这里适用于残差理论等（。一个函数的 “极点”（或孤立的奇点）是指该函数的值变得无界，或 “爆炸 “的一个点。如果一个函数有这样一个极点，那么人们可以在那里计算函数的残差，这可以用来计算涉及该函数的路径积分；这就是强大的残差定理的内容。

my-assignmentexpert™ 复分析complex analysis作业代写，免费提交作业要求， 满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕 博写手团队，所有订单可靠准时，保证 100% 原创。my-assignmentexpert™， 最高质量的复分析complex analysis作业代写，服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。 由于统计Statistics作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此复分析complex analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的复分析complex analysis代写服务。我们的专家在数学mathematics代写方面经验极为丰富，各种复分析complex analysis相关的作业也就用不着 说。

我们提供的复分析complex analysis及其相关学科的代写，服务范围广, 其中包括但不限于:

数学代写|复分析代写complex analysis代考|locally constant

The function $f: G \rightarrow \mathbb{C}$ is said to be locally constant if $f$ is constant in every connected component of $G$.

If the subset $G \subset \mathbb{C}$ is open, and $f \in H(G)$, then the function $f$ is locally constant on $G$ if and only if $f^{\prime}(z)=0, \forall z \in G$.
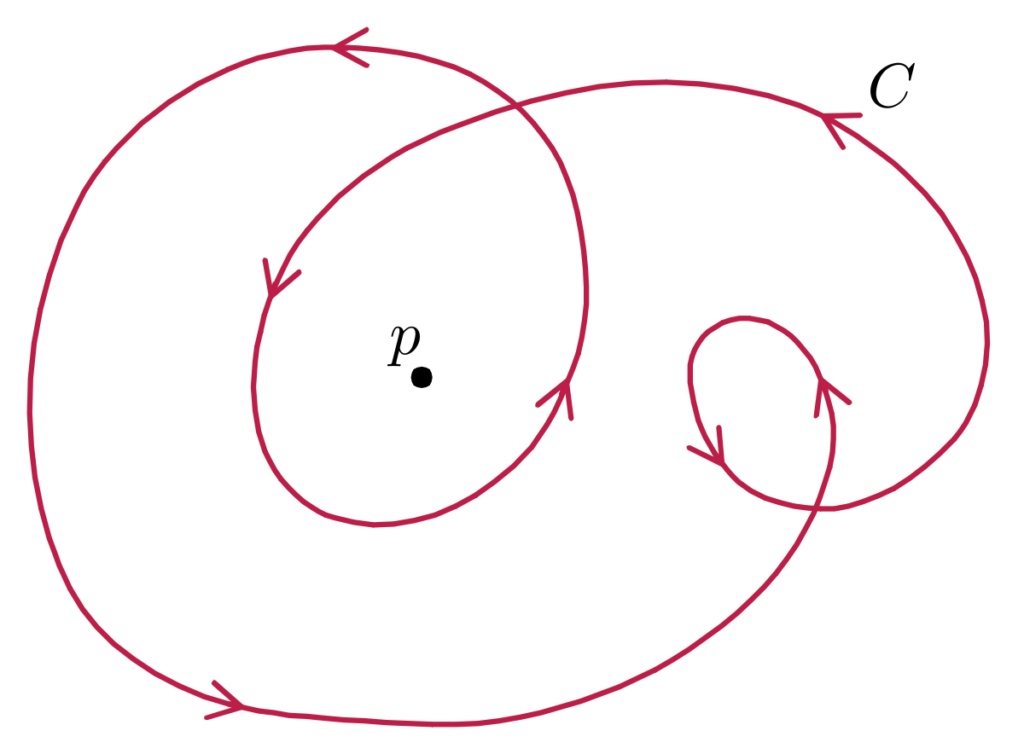
Theorem 3.6.1 (The index theorem). Let $y$ be a rectifiable curve in $\mathbb{C}$.

1. If $\gamma_{1} \underset{\mathrm{C} \backslash\left{z_{0}\right}}{ } \gamma_{2}$, then $\mathrm{n}\left(\gamma_{1}, z_{0}\right)=\mathrm{n}\left(\gamma_{2}, z_{0}\right)$.
2. If $\gamma=y_{1} \cup y_{2}$, then $\mathrm{n}\left(\gamma, z_{0}\right)=\mathrm{n}\left(\gamma_{1}, z_{0}\right)+\mathrm{n}\left(y_{2}, z_{0}\right)$.
3. $\mathrm{n}\left(y^{-}, z_{0}\right)=-\mathrm{n}\left(y, z_{0}\right)$.
   Let $y$ be a rectifiable closed curve in $\mathbb{C}$. Then:
4. If $z_{0} \in \mathbb{C} \backslash{y}$, then $\mathrm{n}\left(\gamma, z_{0}\right) \in \mathbb{Z}$ (integer number).
5. The function $j(z)=\mathrm{n}(\gamma, z)$ is locally constant on $\mathbb{C} \backslash{y}$.
6. If $y=\partial U\left(z_{0} ; r\right)$ and $z \in U\left(z_{0} ; r\right)$, then $\mathrm{n}(\gamma, z)=1$.
7. The set $\mathbb{C} \backslash{y}$ has exactly one not bounded connected component. If $z_{0}$ is an arbitrary point of this not bounded connected component, then $\mathrm{n}\left(\gamma, z_{0}\right)=0$.
8. The set ${z \in \mathbb{C}: \mathrm{n}(y, z) \neq 0}$ is bounded.
   Proof. Point 1 follows immediately from the Cauchy’s theorem.
   Points 2 and 3 are immediate consequences of the properties of the complex integrals.
9. Let $z \in \mathbb{C} \backslash{y}$. The function $f(\zeta)=\frac{1}{\zeta-z}$ is holomorphic on the $\mathbb{C} \backslash{z}$ set, but it has no primitive, since it is not simply connected set. But it has primitive on every simply connected subset of $\mathbb{C} \backslash{z}$. Next, we will divide such an open neighborhood of ${y}$ in the corresponding simply connected domains, such that every one of these components of the function $f$ has a primitive.

数学代写|复分析代写COMPLEX ANALYSIS代考|The function

4. Let $z \in \mathbb{C} \backslash{y}$. The function $f(\zeta)=\frac{1}{\zeta-z}$ is holomorphic on the $\mathbb{C} \backslash{z}$ set, but it has no primitive, since it is not simply connected set. But it has primitive on every simply connected subset of $\mathbb{C} \backslash{z}$. Next, we will divide such an open neighborhood of ${y}$ in the corresponding simply connected domains, such that every one of these components of the function $f$ has a primitive.

Let $\rho=\mathrm{d}(z ;{y})$. Since ${\gamma}$ is a closed set, and $z \notin{y}, \rho>0$, the function $\gamma$ is uniformly continuous on the closed interval $[0,1]$, hence
$$
\exists \eta>0 \text { such that, if }\left|t^{\prime}-t^{\prime \prime}\right|<\eta \text {, then }\left|\gamma\left(t^{\prime}\right)-\gamma\left(t^{\prime \prime}\right)\right|<\rho .
$$
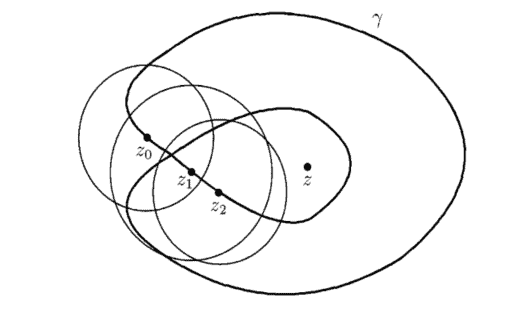
Let us consider the division $\Delta=\left(t_{0}, t_{1}, \ldots, t_{n}\right), 0=t_{0}<t_{1}<\cdots<t_{n}=1$ of the interval $[0,1]$, such that $|\Delta|<\eta$, and let $z_{k}=\gamma\left(t_{k}\right), k \in{0,1, \ldots, n}$. Then $\gamma\left(\left[t_{k}, t_{k+1}\right]\right) \subset U\left(z_{k} ; \rho\right)$, $k=\overline{0, n-1}$. Let $\gamma_{1}, \gamma_{2}, \ldots, \gamma_{n}$ be the decomposition of the curve $\gamma$ corresponding to the division $\Delta$. Then $\left{y_{k}\right}=y\left(\left[t_{k-1}, t_{k}\right]\right) \subset U\left(z_{k-1} ; \rho\right)$, and
$$
\mathrm{n}(\gamma, z)=\frac{1}{2 \pi i} \int_{\gamma} \frac{\mathrm{d} \zeta}{\zeta-z}=\sum_{k=1}^{n} \frac{1}{2 \pi i} \int_{\gamma_{k}} \frac{\mathrm{d} \zeta}{\zeta-z} .
$$
Now we will compute the integrals which appears in this sum. We know that $z_{0}=$ $\gamma(0)$, and let us consider $w_{0} \in \log \left(z_{0}-z\right)$. Now we will use the existence theorem of the analytical branch for the multivalued function Log , for $\log g(\zeta)$, where $g(\zeta)=\zeta-z$, in the $U\left(z_{0} ; \rho\right)$ disc (which is a simply connected domain). It follows that there exists the function $f_{0} \in H\left(U\left(z_{0} ; \rho\right)\right)$, such that
$$
f_{0}^{\prime}(\zeta)=\frac{1}{\zeta-z}, \quad f_{0}(\zeta) \in \log (\zeta-z), \quad \forall \zeta \in U\left(z_{0} ; \rho\right) \text { and } f_{0}\left(z_{0}\right)=w_{0}
$$
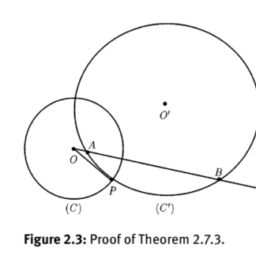
Hence $f_{0}\left(z_{1}\right) \in \log \left(z_{1}-z\right)$, because $z_{1} \in U\left(z_{0} ; \rho\right)$ (Figure 3.4). In the $\operatorname{disc} U\left(z_{1} ; \rho\right)$, we will choose that analytic branch of $\log (\zeta-z)$, denoted by $f_{1}$, such that $f_{1}\left(z_{1}\right)=f_{0}\left(z_{1}\right)$, and we will repeat this algorithm for all the points $z_{2}, \ldots, z_{n}$.

复分析代写

数学代写|复分析代写COMPLEX ANALYSIS代考|LOCALLY CONSTANT

功能F:G→C被称为局部常数，如果F在的每个连通分量中是常数G.

如果子集G⊂C是开放的，并且F∈H(G), 那么函数F是局部常数G当且仅当F′(和)=0,∀和∈G.
定理 3.6.1吨H和一世nd和X吨H和这r和米. 让是是一条可修正的曲线C.

1. 如果\gamma_{1} \underset{\mathrm{C} \backslash\left{z_{0}\right}}{ } \gamma_{2}\gamma_{1} \underset{\mathrm{C} \backslash\left{z_{0}\right}}{ } \gamma_{2}， 然后n(C1,和0)=n(C2,和0).
2. 如果C=是1∪是2， 然后n(C,和0)=n(C1,和0)+n(是2,和0).
3. n(是−,和0)=−n(是,和0).
   让是是一条可修正的闭合曲线C. 然后：
4. 如果和0∈C∖是， 然后n(C,和0)∈从 一世n吨和G和rn你米b和r.
5. 功能j(和)=n(C,和)是局部常数C∖是.
6. 如果是=∂ü(和0;r)和和∈ü(和0;r)， 然后n(C,和)=1.
7. 套装C∖是正好有一个无界连通分量。如果和0是这个无界连通分量的任意点，那么n(C,和0)=0.
8. 套装和∈C:n(是,和)≠0是有界的。
   证明。第 1 点紧随柯西定理。
   第 2 点和第 3 点是复积分性质的直接结果。
9. 让和∈C∖是. 功能F(G)=1G−和是全纯的C∖和集，但它没有原语，因为它不是简单的连接集。但它在每个简单连接的子集上都有原语C∖和. 接下来，我们将这样一个开放的邻域划分为是在相应的简单连接域中，使得函数的这些组件中的每一个F有一个原语。

数学代写|复分析代写COMPLEX ANALYSIS代考|THE FUNCTION

4. 让和∈C∖是. 功能F(G)=1G−和是全纯的C∖和集，但它没有原语，因为它不是简单的连接集。但它在每个简单连接的子集上都有原语C∖和. 接下来，我们将这样一个开放的邻域划分为是在相应的简单连接域中，使得函数的这些组件中的每一个F有一个原语。

让ρ=d(和;是). 自从C是闭集，并且和∉是,ρ>0， 功能C在闭区间上一致连续[0,1]， 因此
∃这>0 这样，如果 |吨′−吨′′|<这， 然后 |C(吨′)−C(吨′′)|<ρ.
让我们考虑划分Δ=(吨0,吨1,…,吨n),0=吨0<吨1<⋯<吨n=1区间的[0,1], 这样|Δ|<这， 然后让和到=C(吨到),到∈0,1,…,n. 然后C([吨到,吨到+1])⊂ü(和到;ρ),到=0,n−1¯. 让C1,C2,…,Cn是曲线的分解C对应分区Δ. 然后\left{y_{k}\right}=y\left(\left[t_{k-1}, t_{k}\right]\right) \subset U\left(z_{k-1} ; \rho \对）\left{y_{k}\right}=y\left(\left[t_{k-1}, t_{k}\right]\right) \subset U\left(z_{k-1} ; \rho \对）， 和
n(C,和)=12圆周率一世∫CdGG−和=∑到=1n12圆周率一世∫C到dGG−和.
现在我们将计算出现在这个总和中的积分。我们知道和0= C(0)，让我们考虑在0∈日志⁡(和0−和). 现在我们将使用多值函数 Log 的解析分支的存在定理，对于日志⁡G(G)， 在哪里G(G)=G−和， 在里面ü(和0;ρ)光盘在H一世CH一世s一种s一世米p一世是C这nn和C吨和dd这米一种一世n. 由此可知存在函数F0∈H(ü(和0;ρ)), 这样
F0′(G)=1G−和,F0(G)∈日志⁡(G−和),∀G∈ü(和0;ρ) 和 F0(和0)=在0
因此F0(和1)∈日志⁡(和1−和)， 因为和1∈ü(和0;ρ) F一世G你r和3.4. 在里面光盘⁡ü(和1;ρ)，我们将选择日志⁡(G−和)，表示为F1, 这样F1(和1)=F0(和1), 我们将对所有点重复这个算法和2,…,和n.

数学代写|复分析代写complex analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

怎么学好数论

图论代写

数论代写

算法代写

随机多项式代写

抽象代数代写