如果你也在 怎样代写理论力学Theoretical Mechanics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。理论力学Theoretical Mechanics是一组密切相关的经典力学的替代公式。它是由许多科学家和数学家在18世纪及以后,在牛顿力学之后发展起来的。由于牛顿力学考虑的是运动的矢量,特别是系统中各组成部分的加速度、动量、力,因此由牛顿定律和欧拉定律所支配的力学的另一个名称是矢量力学。
理论力学Theoretical Mechanics使用代表系统整体的运动标量属性–通常是其总动能和势能–而不是牛顿对单个粒子的矢量力。运动方程是由标量通过一些关于标量变化的基本原理推导出来的。分析力学使用代表系统整体的运动标量属性–通常是其总动能和势能–而不是牛顿对单个粒子的矢量力。运动方程是由标量通过一些关于标量变化的基本原理推导出来的。
my-assignmentexpert™ 理论力学Theoretical Mechanics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的理论力学Theoretical Mechanics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此理论力学Theoretical Mechanics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的理论力学Theoretical Mechanics代写服务。我们的专家在物理physics代写方面经验极为丰富,各种理论力学Theoretical Mechanics相关的作业也就用不着 说。
我们提供的理论力学Theoretical Mechanics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|理论力学作业代写Theoretical Mechanics代考|The Wave Equation of Classical Mechanics
The following considerations are valid for systems with
$$
H=T+V=E=\text { const }
$$
i.e., the Hamilton function is not explicitly time-dependent, and there are no rheonomic constraints. According to (3.45) we can then separate the time-dependence of the action function:
$$
S(\mathbf{q}, \overline{\mathbf{p}}, t)=W(\mathbf{q}, \overline{\mathbf{p}})-E t
$$
Let us remember: $S$ is a generating function of the type $F_{2}$, which takes care for $\bar{H}=0$ and therewith leads to $\overline{\mathbf{p}}=$ const,$\overline{\mathbf{q}}=$ const. The characteristic function $W(\mathbf{q}, \overline{\mathbf{p}})$ is time-independent, and because of $\overline{\mathbf{p}}=\boldsymbol{\alpha}=\mathbf{c o n s t}$ we can conclude:
$$
W=\text { const } \Longleftrightarrow \text { fixed plane in the configuration space }
$$
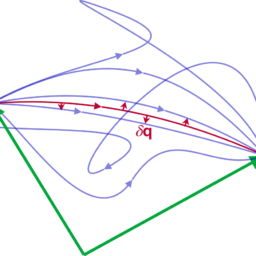
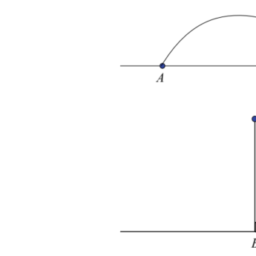
The planes $S=$ const, on the other hand, are moving in the configuration space, shifting themselves in the course of time $t$ over the fixed $W$-planes (Fig. 3.9). They build within the configuration space propagating wave fronts of the so-called
waves of action
We ask ourselves:
- What is the velocity of the propagating $S$-planes?
- What is the physical meaning of the motion of the waves of action?
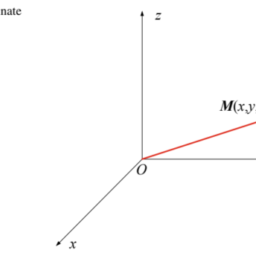
For simplicity we assume that the considered system consists of one single particle,
$$
\mathbf{q}=(x, y, z)
$$
so that the configuration space coincides with the three-dimensional visual space. The
wave velocity $\mathbf{u}$
is the propagation-velocity of a certain point of the front of the wave of action. Since the area of constant $S$ will change its shape as a function of time, the wave velocity will in general not be the same for all points of the wave front. Let us consider two neighboring points in the configuration space and event space, respectively:
$$
\begin{array}{ll}
A=(x, y, z) & \text { at time } t \
B=(x+d x, y+d y, z+d z) & \text { at time } t+d t
\end{array}
$$
物理代写|理论力学作业代写Theoretical Mechanics代考|Insertion About Light Waves
Today one knows that ‘light’ is an electromagnetic process which is described by the
scalar wave equation of optics
$$
\nabla^{2} \varphi-\frac{n^{2}}{c^{2}} \frac{\partial^{2} \varphi}{\partial t^{2}}=0
$$
Here:
$\begin{array}{ll}\varphi: & \text { scalar electromagnetic potential } \ c=3 \cdot 10^{10} \mathrm{~cm} \mathrm{~s}^{-1} & \text { speed of light in vacuum } \ n: & \text { index of refraction, generally } n=n(\mathbf{r}), \ u=c / n: & \text { speed of light in matter } .\end{array}$
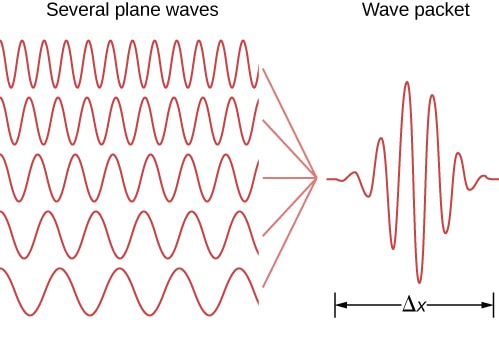
We are looking for simple solutions of the wave equation. For this purpose first we assume
$$
n=\mathrm{const}
$$
Then the following ansatz (plane wave)
$$
\varphi=\varphi_{0} \mathrm{e}^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)}
$$
obviously solves the wave equation provided:
$$
k=\omega \frac{n}{c}=\frac{2 \pi v}{u}=\frac{2 \pi}{\lambda}
$$
Thereby we have exploited
$$
\omega=2 \pi v ; \quad u=v \lambda
$$
The direction of $\mathbf{k}$ (wave vector) may define the $z$-axis. Let $\mathbf{k}{0}$ be the wave vector in vacuum $(n=1)$ : $$ \mathbf{k}=n \mathbf{k}{0} ; \quad \omega=c k_{0}
$$
Therewith we can write the solution (3.190) also as follows:
$$
\varphi=\varphi_{0} \mathrm{e}^{i k_{0}(n z-c t)}
$$
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|The Ansatz of Wave Mechanics
The considerations of the last section suggest the following attempt for a generalization of classical mechanics:
classical mechanics $\Longleftrightarrow$ geometrical-optical limiting case of a wave mechanics
We extend the hitherto theory in the sense that we now interpret the particle motion as wave motion.
We can draw the final justification of this idea of course, if at all, only from a later comparison between theory and experiment. We use, at first only tentatively, the following assignments:
$$
\begin{aligned}
(\nabla W)^{2}=\frac{E^{2}}{u^{2}} & \Longleftrightarrow(\nabla L)^{2}=n^{2} \
W & \Longleftrightarrow L \
\frac{|E|}{u}=\sqrt{2 m(E-V)} & \Longleftrightarrow n=\frac{c}{u} .
\end{aligned}
$$
That does not at all mean that the single terms were exactly equal. They only correspond to each other. For instance, they might be proportional to each other.
理论力学代写
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|THE WAVE EQUATION OF CLASSICAL MECHANICS
以下注意事项适用于具有
H=吨+五=和= 常量
即,Hamilton 函数不是明确的时间相关的,并且没有流变约束。根据3.45然后我们可以分离动作函数的时间依赖性:
小号(q,p¯,吨)=在(q,p¯)−和吨
让我们记住:小号是类型的生成函数F2,它照顾H¯=0并因此导致p¯=常量,q¯=常量。特征函数在(q,p¯)是与时间无关的,并且由于p¯=一种=C这ns吨我们可以得出结论:
在= 常量 ⟺ 配置空间中的固定平面
飞机小号=另一方面,const 在配置空间中移动,随着时间的推移而移动吨在固定的在-计划F一世G.3.9. 它们构建在所谓
的行动波传播波阵面的配置空间内
我们问自己:
- 传播速度是多少小号-计划?
- 作用波运动的物理意义是什么?
为简单起见,我们假设所考虑的系统由一个粒子组成,
q=(X,是,和)
使配置空间与三维视觉空间重合。
波速_你
是作用波前沿某一点的传播速度。由于常数面积小号将随着时间改变其形状,波前的所有点的波速通常不会相同。让我们分别考虑配置空间和事件空间中的两个相邻点:
一种=(X,是,和) 有时 吨 乙=(X+dX,是+d是,和+d和) 有时 吨+d吨
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|INSERTION ABOUT LIGHT WAVES
今天人们知道“光”是一种电磁过程,用
光学的标量波动方程来描述
∇2披−n2C2∂2披∂吨2=0
这里:
披: 标量电磁势 C=3⋅1010 C米 s−1 真空中的光速 n: 折射率,一般 n=n(r), 你=C/n: 物质中的光速 .
我们正在寻找波动方程的简单解。为此,我们首先假设
n=C这ns吨
然后是下面的 ansatzp一世一种n和在一种v和
披=披0和一世(到⋅r−ω吨)
显然解决了所提供的波动方程:
到=ωnC=2圆周率v你=2圆周率λ
因此我们利用了
ω=2圆周率v;你=vλ
的方向到 在一种v和v和C吨这r可以定义和-轴。让 $\mathbf{k} {0}b和吨H和在一种v和v和C吨这r一世nv一种C你你米n=1:$ \mathbf{k}=n \mathbf{k} {0} ; \quad \omega=c k_{0}
吨H和r和在一世吨H在和C一种n在r一世吨和吨H和s这一世你吨一世这n(3.190)一种一世s这一种sF这一世一世这在s:
\varphi=\varphi_{0} \mathrm{e}^{ik_{0}n和−C吨}
$$
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|THE ANSATZ OF WAVE MECHANICS
上一节的考虑提出了以下对经典力学进行概括的尝试:
经典力学⟺波力学的几何光学极限情况
我们扩展了迄今为止的理论,我们现在将粒子运动解释为波动。
当然,如果有的话,我们只能从后来的理论和实验之间的比较中得出这个想法的最终证明。我们最初只是暂时使用以下分配:
(∇在)2=和2你2⟺(∇大号)2=n2 在⟺大号 |和|你=2米(和−五)⟺n=C你.
这根本不意味着单个术语完全相等。它们只是相互对应。例如,它们可能彼此成比例。

物理代写|理论力学作业代写Theoretical Mechanics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。