如果你也在 怎样代写电动力学electrodynamics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。电动力学electrodynamics是物理学的一个分支,涉及到对电磁力的研究,这是一种发生在带电粒子之间的物理作用。电磁力是由电场和磁场组成的电磁场所承载的,它是诸如光这样的电磁辐射的原因。它与强相互作用、弱相互作用和引力一起,是自然界的四种基本相互作用(通常称为力)之一。
电动力学electrodynamics电磁现象是以电磁力来定义的,有时也称为洛伦兹力,它包括电和磁,是同一现象的不同表现形式。电磁力在决定日常生活中遇到的大多数物体的内部属性方面起着重要作用。原子核和其轨道电子之间的电磁吸引力将原子固定在一起。电磁力负责原子之间形成分子的化学键,以及分子间的力量。电磁力支配着所有的化学过程,这些过程是由相邻原子的电子之间的相互作用产生的。电磁学在现代技术中应用非常广泛,电磁理论是电力工程和电子学包括数字技术的基础。
my-assignmentexpert™ 电动力学electrodynamics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的电动力学electrodynamics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此电动力学electrodynamics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的电动力学electrodynamics代写服务。我们的专家在物理physics代写方面经验极为丰富,各种电动力学electrodynamics相关的作业也就用不着 说。
我们提供的电动力学electrodynamics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|电动力学作业代electrodynamics代考|Point Charge Near a Conducting Sphere
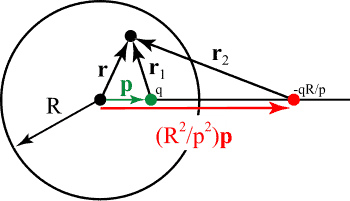
Let us now explicitly solve a slightly more difficult problem of a point charge near a ‘grounded’ conducting sphere of radius $R$, centered at the origin (Fig. 2.4). Suppose the charge $q$ is placed at a point $\mathbf{y}$ outside the sphere. The image charge needs to be placed outside the region of interest, i.e., anywhere inside the sphere. The sign and magnitude of the image charge $q^{\prime}$ and its location $\mathbf{y}^{\prime}$ should be such that the potential $\Phi(\mathbf{x})$ is zero on the surface of the sphere, i.e., for $|\mathbf{x}|=R$. By symmetry, we should place the image charge $q^{\prime}$ somewhere inside the sphere on the straight line connecting the origin and the charge $q$. Or in other words, the position vectors $\mathbf{y}$ and $\mathbf{y}^{\prime}$ should be parallel to each other.
The potential due to the charges $q$ and $q^{\prime}$ anywhere outside the sphere is given by
$$
\Phi(\mathbf{x})=\frac{q}{|\mathbf{x}-\mathbf{y}|}+\frac{q^{\prime}}{\left|\mathbf{x}-\mathbf{y}^{\prime}\right|}
$$
We now choose $q^{\prime}$ such that the required boundary condition $\Phi(\mathbf{x})=0$ for $|\mathbf{x}|=R$ is satisfied
$$
\frac{q^{\prime}}{\left|\mathbf{x}-\mathbf{y}^{\prime}\right|}=-\frac{q}{|\mathbf{x}-\mathbf{y}|}
$$
Therefore,
$$
\frac{q^{\prime 2}}{q}=\frac{\left(\mathbf{x}-\mathbf{y}^{\prime}\right)^{2}}{(\mathbf{x}-\mathbf{y})^{2}}
$$
If $\theta$ is the angle between $\mathbf{x}$ and $\mathbf{y}$ (or $\mathbf{y}^{\prime}$ ), then we have for $|\mathbf{x}|=R$,
$$
2 R\left[y^{\prime}-\left(\frac{q^{\prime}}{q}\right)^{2} y\right] \cos \theta+\left(\frac{q^{\prime}}{q}\right)^{2}\left(R^{2}+y^{2}\right)-\left(R^{2}+y^{\prime 2}\right)=0 .
$$
物理代写|电动力学作业代electrodynamics代考|Conducting Sphere in Uniform Electric Field
The problem of conducting sphere in a uniform electric field can be solved very easily now with the method of images. We assume that the uniform electric field is produced by an appropriate combination of two charges with opposite signs at an appropriate distance. Let us try to find out the magnitude and location of the charges which lead to a uniform electric field around the conducting sphere.
We place a charge $-Q$ at $\mathbf{y}$ and another charge $+Q$ at $-\mathbf{y}$ outside the spherical region as shown in Fig. 2.7. The electric field at an arbitrary point $\mathcal{P}$ due to the combination of the two charges is given by
$$
\mathbf{E}(\mathbf{x})=Q\left[\frac{\mathbf{x}+\mathbf{y}}{|\mathbf{x}+\mathbf{y}|^{3}}-\frac{\mathbf{x}-\mathbf{y}}{|\mathbf{x}-\mathbf{y}|^{3}}\right]
$$
If the charges are far away from the spherical region and from the observation point, i.e., if $|\mathbf{y}| \gg R,|\mathbf{x}|$, we have $\frac{1}{|\mathbf{x} \pm \mathbf{y}|^{3}}=\frac{1}{\left(x^{2}+y^{2} \pm 2 \mathbf{x} \cdot \mathbf{y}\right)^{\frac{3}{2}}}=\frac{1}{y^{3}} \frac{1}{\left(1+\frac{y^{2}}{y^{2}} \pm 2 \frac{x}{y} \mathbf{x} \cdot \mathbf{y}\right)^{\frac{3}{2}}} \approx \frac{1}{y^{3}}$. As a result, the electric field becomes effectively independent of $\mathbf{x}$ in a limited region where $\mathbf{E}(\mathbf{x})=\frac{2 Q}{y^{2}} \hat{\mathbf{y}}^{2}$ Now suppose a conducting sphere is placed at the origin. The image charges corresponding to the point charges $\pm Q$ located at $\mathbf{y}=\mp r^{\prime} \hat{\mathbf{y}}$ are $\mp \frac{Q R}{r^{\prime}}$, located at $\mp y=\frac{R^{2}}{r^{\prime}}$, respectively. The potential due to all four charges anywhere in the region of interest at a distance $|\mathbf{x}|=r$ from the origin is given by
$$
\begin{aligned}
\Phi(\mathbf{r})=& \frac{Q}{\sqrt{r^{2}+r^{\prime 2}+2 r r^{\prime} \cos \theta}}-\frac{Q}{\sqrt{r^{2}+r^{\prime 2}-2 r r^{\prime} \cos \theta}} \
&+\frac{Q R / r^{\prime}}{\sqrt{r^{2}+\left(\frac{R^{2}}{r^{\prime}}\right)^{2}-2 r \frac{R^{2}}{r^{\prime}} \cos \theta}}-\frac{}{\sqrt{r^{2}+\left(\frac{R^{2}}{r^{\prime}}\right)^{2}+2 r \frac{R^{2}}{r^{\prime}} \cos \theta}} .
\end{aligned}
$$
电动力学代写
物理代写|电动力学作业代ELECTRODYNAMICS代考|POINT CHARGE NEAR A CONDUCTING SPHERE
现在让我们明确地解决一个稍微困难的问题,即在半径为“接地”的导电球体附近的点电荷R, 以原点为中心F一世G.2.4. 假设电荷q被放置在一个点是球体之外。图像电荷需要放置在感兴趣区域之外,即球体内的任何位置。图像电荷的符号和大小q′及其位置是′应该是这样的,潜在的披(X)在球体表面上为零,即,对于|X|=R. 通过对称性,我们应该放置图像电荷q′在连接原点和电荷的直线上的球内某处q. 或者换句话说,位置向量是和是′应该相互平行。
电荷的潜力q和q′球体外的任何地方都由
披(X)=q|X−是|+q′|X−是′|
我们现在选择q′使得所需的边界条件披(X)=0为了|X|=R满意
q′|X−是′|=−q|X−是|
所以,
q′2q=(X−是′)2(X−是)2
如果θ是之间的角度X和是 这r$是′$,那么我们有|X|=R,
2R[是′−(q′q)2是]某物θ+(q′q)2(R2+是2)−(R2+是′2)=0.
物理代写|电动力学作业代ELECTRODYNAMICS代考|CONDUCTING SPHERE IN UNIFORM ELECTRIC FIELD
现在用图像的方法可以很容易地解决均匀电场中导电球的问题。我们假设均匀电场是由在适当距离处具有相反符号的两个电荷的适当组合产生的。让我们试着找出导致导电球周围均匀电场的电荷的大小和位置。
我们收取费用−问在是和另一笔费用+问在−是如图 2.7 所示。任意点的电场磷由于这两种费用的组合由下式给出
和(X)=问[X+是|X+是|3−X−是|X−是|3]
如果电荷远离球面区域和观察点,即如果|是|≫R,|X|, 我们有1|X±是|3=1(X2+是2±2X⋅是)32=1是31(1+是2是2±2X是X⋅是)32≈1是3. 结果,电场变得有效地独立于X在有限的区域内和(X)=2问是2是^2现在假设在原点放置一个导电球。点电荷对应的像电荷±问位于是=∓r′是^是∓问Rr′, 位于∓是=R2r′, 分别。由于所有四种电荷在远处感兴趣区域的任何地方产生的电势|X|=r从原点给出
披(r)=问r2+r′2+2rr′某物θ−问r2+r′2−2rr′某物θ +问R/r′r2+(R2r′)2−2rR2r′某物θ−r2+(R2r′)2+2rR2r′某物θ.

物理代写|电动力学作业代写electrodynamics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。