如果你也在 怎样代写凸分析Convex Analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。凸分析Convex Analysis是数学的一个分支,专门研究凸函数和凸集的属性,通常应用于凸最小化,这是优化理论的一个子领域。
my-assignmentexpert™ 凸分析Convex Analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的凸分析Convex Analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此凸分析Convex Analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的凸分析Convex Analysis作业代写代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种凸分析Convex Analysis相关的作业也就用不着 说。
我们提供的凸分析Convex Analysis及其相关学科的代写,服务范围广, 其中包括但不限于:、
- 优化理论 optimization theory
- 变分法 Calculus of variations
- 最优控制理论 Optimal control
- 动态规划 Dynamic programming
- 鲁棒优化 Robust optimization
- 随机优化 Stochastic programming
- 组合优化 Combinatorial optimization
数学代考|凸分析作业代写Convex Analysis代考|Subgradients and Convex Functions
We have already seen, in the First order sufficient condition (2.1.2), one benefit of convexity in optimization: critical points of convex functions are global minimizers. In this section we extend the types of functions we consider in two important ways:
(i) We do not require $f$ to be differentiable.
(ii) We allow $f$ to take the value $+\infty$.
Our derivation of first order conditions in Section $2.3$ illustrates the utility of considering nonsmooth functions even in the context of smooth problems. Allowing the value $+\infty$ lets us rephrase a problem like
$$
\inf \{g(x) \mid x \in C\}
$$
as $\inf \left(g+\delta_{C}\right)$, where the indicator function $\delta_{C}(x)$ is 0 for $x$ in $C$ and $+\infty$ otherwise.
The domain of a function $f: \mathbf{E} \rightarrow(\infty,+\infty]$ is the set
$$
\operatorname{dom} f=\{x \in \mathbf{E} \mid f(x)<+\infty\}
$$
数学代考|凸分析作业代写Convex Analysis代考|The Value Function
In this section we describe another approach to the Karush-Kuhn-Tucker conditions (2.3.8) in the convex case using the existence of subgradients we established in the previous section. We consider an (inequality-constrained) convex program
$$
\inf \left\{f(x) \mid g_{i}(x) \leq 0 \text { for } i=1,2, \ldots, m, x \in \mathbf{E}\right\}
$$
where the functions $f, g_{1}, g_{2}, \ldots, g_{m}: \mathbf{E} \rightarrow(\infty,+\infty]$ are convex and satisfy $\emptyset \neq \operatorname{dom} f \subset \cap_{i} \operatorname{dom} g_{i}$. Denoting the vector with components $g_{i}(x)$ by $g(x)$, the function $L: \mathbf{E} \times \mathbf{R}_{+}^{m} \rightarrow(\infty,+\infty]$ defined by
$$
L(x ; \lambda)=f(x)+\lambda^{T} g(x)
$$
is called the Lagrangian. A feasible solution is a point $x$ in dom $f$ satisfying the constraints.
We should emphasize that the term “Lagrange multiplier” has different meanings in different contexts. In the present context we say a vector $\bar{\lambda} \in$ $\mathbf{R}_{+}^{m}$ is a Lagrange multiplier vector for a feasible solution $\bar{x}$ if $\bar{x}$ minimizes the function $L(\cdot ; \bar{\lambda})$ over $\mathbf{E}$ and $\bar{\lambda}$ satisfies the complementary slackness conditions: $\bar{\lambda}_{i}=0$ whenever $g_{i}(\bar{x})<0$.
We can often use the following principle to solve simple optimization problems.
数学代考|凸分析作业代写Convex Analysis代考|The Fenchel Conjugate
In the next few sections we sketch a little of the elegant and concise theory of Fenchel conjugation, and we use it to gain a deeper understanding of the Lagrangian necessary conditions for convex programs (3.2.8). The Fenchel conjugate of a function $h: \mathbf{E} \rightarrow[-\infty,+\infty]$ is the function $h^{*}: \mathbf{E} \rightarrow$ $[-\infty,+\infty]$ defined by
$$
h^{*}(\phi)=\sup _{x \in \mathbf{E}}\{\langle\phi, x\rangle-h(x)\} .
$$
The function $h^{*}$ is convex and if the domain of $h$ is nonempty then $h^{*}$ never takes the value $-\infty$. Clearly the conjugacy operation is order-reversing: for functions $f, g: \mathbf{E} \rightarrow[-\infty,+\infty]$, the inequality $f \geq g$ implies $f^{*} \leq g^{*}$.
Conjugate functions are ubiquitous in optimization. For example, we have already seen the conjugate of the exponential, defined by
$$
\exp ^{*}(t)= \begin{cases}t \log t-t & \text { if } t>0 \\ 0 & \text { if } t=0 \\ +\infty & \text { if } t<0\end{cases}
$$
(see Section 3.1, Exercise 27). A rather more subtle example is the function $g: \mathbf{E} \rightarrow(\infty,+\infty]$ defined, for points $a^{0}, a^{1}, \ldots, a^{m}$ in $\mathbf{E}$, by
$$
g(z)=\inf _{x \in \mathbf{R}^{m+1}}\left\{\sum_{i} \exp ^{*}\left(x_{i}\right) \mid \sum_{i} x_{i}=1, \sum_{i} x_{i} a^{i}=z\right\} .
$$
The conjugate is the function we used in Section $2.2$ to prove various theorems of the alternative:
$$
g^{*}(y)=1+\log \left(\sum_{i} \exp \left\langle a^{i}, y\right\rangle\right)
$$
(see Exercise 7).
As we shall see later (Section 4.2), many important convex functions $h$ equal their biconjugates $h^{* *}$. Such functions thus occur as natural pairs, $h$ and $h^{*}$. Table $3.1$ shows some elegant examples on $\mathbf{R}$, and Table $3.2$ describes some simple transformations of these examples.
The following result summarizes the properties of two particularly important convex functions.
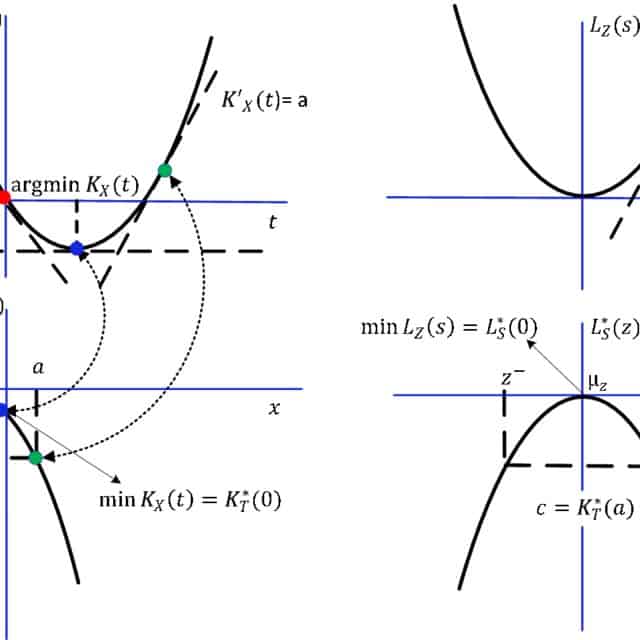
数学代考|凸分析作业代写CONVEX ANALYSIS代考|SUBGRADIENTS AND CONVEX FUNCTIONS
我们已经看到,在一阶充分条件下2.1.2,优化中凸性的一个好处:凸函数的临界点是全局最小化器。在本节中,我们以两种重要的方式扩展了我们考虑的函数类型:
一世我们不需要F可微分。
一世一世我们允许F取值+∞.
我们在部分一阶条件的推导2.3说明即使在光滑问题的上下文中考虑非光滑函数的效用。允许值+∞让我们改写一个问题,比如
信息{G(X)∣X∈C}
作为信息(G+dC), 其中指标函数dC(X)为 0X在C和+∞除此以外。
函数的域F:和→(∞,+∞]是集合
判断F={X∈和∣F(X)<+∞}
数学代考|凸分析作业代写CONVEX ANALYSIS代考|THE VALUE FUNCTION
在本节中,我们描述了 Karush-Kuhn-Tucker 条件的另一种方法2.3.8在凸的情况下使用我们在上一节中建立的次梯度的存在。我们考虑一个一世n和q你一种一世一世吨是−C这ns吨r一种一世n和d凸程序
信息{F(X)∣G一世(X)≤0 为了 一世=1,2,…,米,X∈和}
函数在哪里F,G1,G2,…,G米:和→(∞,+∞]是凸的并且满足∅≠判断F⊂∩一世判断G一世. 用分量表示向量G一世(X)经过G(X), 功能大号:和×R+米→(∞,+∞]被定义为
大号(X;λ)=F(X)+λ吨G(X)
称为拉格朗日。一个可行的解决方案是一个点X和家F满足约束。
需要强调的是,“拉格朗日乘数”一词在不同的语境中有不同的含义。在目前的上下文中,我们说一个向量λ¯∈ R+米是可行解的拉格朗日乘数向量X¯如果X¯最小化函数大号(⋅;λ¯)超过和和λ¯满足互补松弛条件:λ¯一世=0每当G一世(X¯)<0.
我们经常可以使用以下原则来解决简单的优化问题。
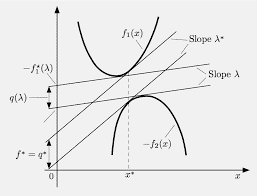
数学代考|凸分析作业代写CONVEX ANALYSIS代考|THE FENCHEL CONJUGATE
在接下来的几节中,我们将简要介绍一下 Fenchel 共轭的优雅和简洁的理论,并使用它来更深入地理解凸规划的拉格朗日必要条件3.2.8. 函数的 Fenchel 共轭H:和→[−∞,+∞]是函数H∗:和→ [−∞,+∞]被定义为
H∗(φ)=支持X∈和{⟨φ,X⟩−H(X)}.
功能H∗是凸的,如果域H那么是非空的H∗从不取值−∞. 显然,共轭运算是逆序的:对于函数F,G:和→[−∞,+∞], 不等式F≥G暗示F∗≤G∗.
共轭函数在优化中无处不在。例如,我们已经看到了指数的共轭,定义为
经验∗(吨)={吨日志吨−吨 如果 吨>00 如果 吨=0+∞ 如果 吨<0
s和和小号和C吨一世这n3.1,和X和rC一世s和27. 一个更微妙的例子是函数G:和→(∞,+∞]已定义,用于点一种0,一种1,…,一种米在和, 经过
G(和)=信息X∈R米+1{∑一世经验∗(X一世)∣∑一世X一世=1,∑一世X一世一种一世=和}.
conjugate 是我们在 Section 中使用的函数2.2证明替代的各种定理:
G∗(是)=1+日志(∑一世经验⟨一种一世,是⟩)
s和和和X和rC一世s和7.
我们稍后会看到小号和C吨一世这n4.2, 许多重要的凸函数H等于他们的双共轭H∗∗. 因此,这些功能以自然对的形式出现,H和H∗. 桌子3.1展示了一些优雅的例子R, 和表3.2描述了这些示例的一些简单转换。
下面的结果总结了两个特别重要的凸函数的性质。

数学代考|凸分析作业代写Convex Analysis代考 请认准UpriviateTA. UpriviateTA为您的留学生涯保驾护航。
更多内容请参阅另外一份复分析代写.