如果你也在 怎样代写凸分析Convex Analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。凸分析Convex Analysis是数学的一个分支,专门研究凸函数和凸集的属性,通常应用于凸最小化,这是优化理论的一个子领域。
my-assignmentexpert™ 凸分析Convex Analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的凸分析Convex Analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此凸分析Convex Analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的凸分析Convex Analysis作业代写代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种凸分析Convex Analysis相关的作业也就用不着 说。
我们提供的凸分析Convex Analysis及其相关学科的代写,服务范围广, 其中包括但不限于:、
- 优化理论 optimization theory
- 变分法 Calculus of variations
- 最优控制理论 Optimal control
- 动态规划 Dynamic programming
- 鲁棒优化 Robust optimization
- 随机优化 Stochastic programming
- 组合优化 Combinatorial optimization
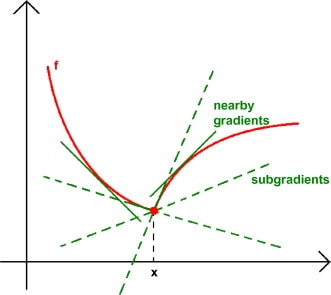
数学代考|凸分析作业代写Convex Analysis代考|Generalized Derivatives
From the perspective of optimization, the subdifferential $\partial f(\cdot)$ of a convex function $f$ has many of the useful properties of the derivative. Some examples: it gives the necessary optimality condition $0 \in \partial f(x)$ when the point $x$ is a (local) minimizer (Proposition 3.1.5); it reduces to $\{\nabla f(x)\}$ when $f$ is differentiable at $x$ (Corollary $3.1 .10$ ); and it often satisfies certain calculus rules such as $\partial(f+g)(x)=\partial f(x)+\partial g(x)$ (Theorem 3.3.5). For a variety of reasons, if the function $f$ is not convex, the subdifferential $\partial f(\cdot)$ is not a particularly helpful idea. This makes it very tempting to look for definitions of the subdifferential for a nonconvex function. In this section we outline some examples; the most appropriate choice often depends on context.
For a convex function $f: \mathbf{E} \rightarrow(\infty,+\infty]$ with $x$ in $\operatorname{dom} f$, we can characterize the subdifferential via the directional derivative: $\phi \in \partial f(x)$ if and only if $\langle\phi, \cdot\rangle \leq f^{\prime}(x ; \cdot)$ (Proposition 3.1.6). A natural approach is therefore to generalize the directional derivative. Henceforth in this section we make the simplifying assumption that the real function $f$ (a real-valued function defined on some subset of $\mathbf{E}$ ) is locally Lipschitz around the point $x$ in $\mathbf{E}$.
Partly motivated by the development of optimality conditions, a simple first try is the Dini directional derivative:
$$
f^{-}(x ; h)=\liminf _{t \downarrow 0} \frac{f(x+t h)-f(x)}{t} .
$$
数学代考|凸分析作业代写Convex Analysis代考|Regularity and Strict Differentiability
We have outlined in Section $2.3$ and Section $3.2$ two very distinct versions of the necessary optimality conditions in constrained optimization. The first, culminating in the Karush-Kuhn-Tucker conditions (2.3.8), relied on Gâteaux differentiability, while the second, leading to the Lagrangian necessary conditions (3.2.8), used convexity. A primary aim of the nonsmooth theory of this chapter is to unify these types of results; in this section we show how this is possible.
A principal feature of the Michel-Penot subdifferential is that it coincides with the Gâteaux derivative when this exists.
数学代考|凸分析作业代写Convex Analysis代考|The Limiting Subdifferential
We simplified our brief outline of some of the fundamental ideas of nonsmooth analysis by restricting attention to locally Lipschitz functions. By contrast, the convex analysis we have developed lets us study the optimization problem inf $\{f(x) \mid x \in S\}$ via the function $f+\delta_{S}$, even though the indicator function $\delta_{S}$ is not locally Lipschitz on the boundary of the set $S$. The following simple but very important idea circumvents this difficulty. We define the distance function to the nonempty set $S \subset \mathbf{E}$ by
$$
d_{S}(x)=\inf \{\|y-x\| \mid y \in S\}
$$
(see Section 3.3, Exercise 12 (Infimal convolution).) We can easily check that $d_{S}$ has Lipschitz constant equal to one on $\mathbf{E}$, and is convex if and only if $S$ has convex closure.
数学代考|凸分析作业代写Convex Analysis代考|Convex Process Duality
In this chapter we have seen a variety of subdifferentials. As we have observed, the smaller the subdifferential, the stronger the necessary optimality conditions we obtain by using it. On the other hand, the smallest of our subdifferentials, the Dini subdifferential, is in some sense too small. It may be empty, it is not a closed multifunction, and it may not always satisfy a sum rule:
$$
\partial_{-}(f+g)(x) \not \subset \partial_{-} f(x)+\partial_{-} g(x)
$$
in general. In this section we show how to enlarge it somewhat to construct what is, in many senses, the smallest adequate closed subdifferential.
Consider for the moment a real function $f$ that is locally Lipschitz around the point $x$ in $\mathbf{E}$. Using a construction analogous to the Intrinsic Clarke subdifferential theorem (6.2.5), we can construct a nonempty subdifferential incorporating the local information from the Dini subdifferential. Specifically, we define the limiting subdifferential by closing the graph of the Dini subdifferential:
$$
\partial_{a} f(x)=\left\{\lim _{r} \phi^{r} \mid x^{r} \rightarrow x, \phi^{r} \in \partial_{-} f\left(x^{r}\right)\right\} .
$$
(Recall $\partial_{-} f(z)$ is nonempty at points $z$ arbitrarily close to $x$ by Section 6.2, Exercise 13.) We sketch some of the properties of the limiting subdifferential in the exercises. In particular, it is nonempty and compact, it coincides with $\partial f(x)$ when $f$ is convex and continuous at the point $x$, and any local minimizer $x$ of $f$ must satisfy $0 \in \partial_{a} f(x)$. Often the limiting subdifferential is not convex; in fact its convex hull is exactly the Clarke subdifferential. A harder fact is that if the real function $g$ is also locally Lipschitz around $x$ then a sum rule holds:
$$
\partial_{a}(f+g)(x) \subset \partial_{a} f(x)+\partial_{a} g(x) .
$$
数学代考|凸分析作业代写CONVEX ANALYSIS代考|GENERALIZED DERIVATIVES
从优化的角度来看,次微分∂F(⋅)凸函数的F具有衍生的许多有用特性。一些例子:它给出了必要的最优性条件0∈∂F(X)当点X是一个一世这C一种一世最小化器磷r这p这s一世吨一世这n3.1.5; 它减少到{∇F(X)}什么时候F可微分于X C这r这一世一世一种r是$3.1.10$; 它通常满足某些微积分规则,例如∂(F+G)(X)=∂F(X)+∂G(X) 吨H和这r和米3.3.5. 由于各种原因,如果函数F不是凸的,次微分∂F(⋅)不是一个特别有用的想法。这使得寻找非凸函数的次微分定义变得非常诱人。在本节中,我们概述了一些示例;最合适的选择通常取决于上下文。
对于凸函数F:和→(∞,+∞]和X在判断F,我们可以通过方向导数来表征次微分:φ∈∂F(X)当且仅当⟨φ,⋅⟩≤F′(X;⋅) 磷r这p这s一世吨一世这n3.1.6. 因此,一种自然的方法是推广方向导数。此后在本节中,我们做出简化假设,即实函数F 一种r和一种一世−v一种一世你和dF你nC吨一世这nd和F一世n和d这ns这米和s你bs和吨这F$和$在该点附近是局部 LipschitzX在和.
部分受优化条件发展的推动,一个简单的第一次尝试是 Dini 方向导数:
F−(X;H)=林inf吨↓0F(X+吨H)−F(X)吨.
数学代考|凸分析作业代写CONVEX ANALYSIS代考|REGULARITY AND STRICT DIFFERENTIABILITY
我们已经在第2.3和部分3.2约束优化中必要最优性条件的两个非常不同的版本。第一个,在 Karush-Kuhn-Tucker 条件下达到高潮2.3.8, 依赖于 Gâteaux 可微性, 而第二个, 导致拉格朗日必要条件3.2.8, 使用凸度。本章非光滑理论的主要目的是统一这些类型的结果。在本节中,我们将展示这是如何实现的。
Michel-Penot 次微分的一个主要特征是,当它存在时,它与 Gâteaux 导数一致。
数学代考|凸分析作业代写CONVEX ANALYSIS代考|THE LIMITING SUBDIFFERENTIAL
我们通过将注意力限制在局部 Lipschitz 函数上,简化了对非光滑分析的一些基本思想的简要概述。相比之下,我们开发的凸分析让我们研究优化问题 inf{F(X)∣X∈小号}通过函数F+d小号, 即使指标函数d小号不是在集合边界上的局部 Lipschitz小号. 以下简单但非常重要的想法绕过了这个困难。我们定义到非空集的距离函数小号⊂和经过
d小号(X)=信息{‖是−X‖∣是∈小号}
s和和小号和C吨一世这n3.3,和X和rC一世s和12(一世nF一世米一种一世C这nv这一世你吨一世这n.) 我们可以很容易地检查d小号有 Lipschitz 常数等于 1和, 并且是凸的当且仅当小号有凸闭合。
数学代考|凸分析作业代写CONVEX ANALYSIS代考|CONVEX PROCESS DUALITY
在本章中,我们看到了各种次微分。正如我们所观察到的,次微分越小,我们通过使用它获得的必要最优性条件就越强。另一方面,我们最小的次微分,Dini 次微分,在某种意义上太小了。它可能是空的,它不是一个封闭的多功能,它可能并不总是满足求和规则:
$$
\partial_{-}(f+g)(x) \not \subset \partial_{-} f(x)+\partial_{-} g(x)
$$
in general. In this section we show how to enlarge it somewhat to construct what is, in many senses, the smallest adequate closed subdifferential.
Consider for the moment a real function $f$ that is locally Lipschitz around the point $x$ in $\mathbf{E}$. Using a construction analogous to the Intrinsic Clarke subdifferential theorem (6.2.5), we can construct a nonempty subdifferential incorporating the local information from the Dini subdifferential. Specifically, we define the limiting subdifferential by closing the graph of the Dini subdifferential:
$$
\partial_{a} f(x)=\left{\lim {r} \phi^{r} \mid x^{r} \rightarrow x, \phi^{r} \in \partial{-} f\left(x^{r}\right)\right} .
$$
(Recall $\partial_{-} f(z)$ is nonempty at points $z$ arbitrarily close to $x$ by Section 6.2, Exercise 13.) We sketch some of the properties of the limiting subdifferential in the exercises. In particular, it is nonempty and compact, it coincides with $\partial f(x)$ when $f$ is convex and continuous at the point $x$, and any local minimizer $x$ of $f$ must satisfy $0 \in \partial_{a} f(x)$. Often the limiting subdifferential is not convex; in fact its convex hull is exactly the Clarke subdifferential. A harder fact is that if the real function $g$ is also locally Lipschitz around $x$ then a sum rule holds:
$$
\partial_{a}(f+g)(x) \subset \partial_{a} f(x)+\partial_{a} g(x) .
$$

数学代考|凸分析作业代写Convex Analysis代考 请认准UpriviateTA. UpriviateTA为您的留学生涯保驾护航。
更多内容请参阅另外一份复分析代写.