如果你也在 怎样代写宏观经济学Macroeconomics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。宏观经济学Macroeconomics(来自希腊语前缀makro-,意思是 “大 “+经济学)是经济学的一个分支,处理整个经济体的表现、结构、行为和决策。例如,使用利率、税收和政府支出来调节经济的增长和稳定。这包括区域、国家和全球经济。根据经济学家Emi Nakamura和Jón Steinsson在2018年的评估,经济 “关于不同宏观经济政策的后果的证据仍然非常不完善,可以受到严重批评。
宏观经济学Macroeconomics研究的主题包括GDP(国内生产总值)、失业(包括失业率)、国民收入、价格指数、产出、消费、通货膨胀、储蓄、投资、能源、国际贸易和国际金融。宏观经济学和微观经济学是经济学中最普遍的两个领域。联合国可持续发展目标17有一个目标,即通过政策协调和一致性来加强全球宏观经济稳定,这是2030年议程的一部分。
my-assignmentexpert™ 宏观经济学Macroeconomics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的宏观经济学Macroeconomics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此宏观经济学Macroeconomics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的宏观经济学Macroeconomics代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种宏观经济学Macroeconomics相关的作业也就用不着 说。
我们提供的宏观经济学Macroeconomics及其相关学科的代写,服务范围广, 其中包括但不限于:
经济代写|宏观经济学作业代写Macroeconomics代考|Cointegration and Error Correction Models
To explain why the spurious results disappear when dynamic models are estimated let us consider a simplified version of the dynamic specification estimated for consumption:
$$
c_{t}=a_{0}+a_{1} c_{t-1}+a_{2} y_{t}+a_{3} y_{t-1}+u_{t}
$$
This specification has some interesting dynamic properties which are worth discussing. First note that the short-run elasticity of consumption with respect to income is different from the long-run elasticity. In fact the short-run elasticity is $a_{2}$ while the long-run elasticity is $\frac{a_{2}+a_{3}}{1-a_{1}}$. The long-run elasticity is found by setting all variables in the dynamic model (2.14) to their steady state value $c_{t+i}=\bar{c}, y_{t+i}=\bar{c}$. To see immediately this point consider the following reparameterisation of :
$$
\begin{aligned}
\Delta c_{t} &=a_{0}+a_{2} \Delta y_{t}-\alpha\left(c_{t-1}-\beta_{1} y_{t-1}\right)+u_{t} \
\alpha &=\left(1-a_{1}\right), \beta_{1}=\frac{a_{2}+a_{3}}{1-a_{1}}
\end{aligned}
$$
The estimated dynamic model includes both first differences and levels. The presence of the level variables generates a long-run solution, derived by setting all first differences either to zero (steady-state with no deterministic trend) or to a constant(steady-state). Note now the role of the terms in level: we can interpret $\beta_{1} y_{t-1}$ as the long-run equilibrium level $c^{}$ for the log of real consumption $c$. When $\alpha<0$ consumption increases at time t whenever $c_{t-1}}$, and decreases whenever $c_{t-1}>c_{t-1}^{}$. The system equilibrates in presence of disequilibrium (i.e. a discrepancy between $c$ and $c^{}$ ) such error correction features guarantees that in the long-run the consumption will converge to its equilibrium value. For this reason the specification (2.15), with $\alpha<0$, is termed Error Correction Model. Note that, in the case of an ECM representation, the difference between $c$ and $c^{*}$ is a stationary series. This defines co-integration. We say that two non stationary variables integrated of order $q$ are cointegrated of order $p$ if there exist a linear combination of them which is integrated of order $p-q$. The case $p=1, q=1$, is interesting in that co-integration implies an ECM representation, which allows to re-write a model in levels, which involves non-stationary time-series, as a model which involves only stationary variables. Such variables are stationary either because they are first diferences of non-stationary variables or because they are stationary linear combination of non-stationary variables (cointegrating vectors).
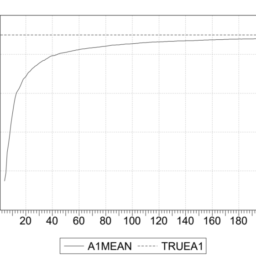
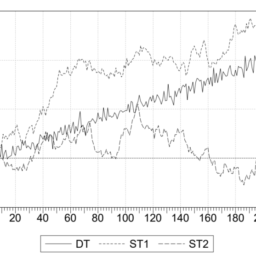
The inclusion of both differences and levels in the estimated relationship is the key factor to the solution of the problems related to non-stationarity of the level of variables included in the specification. This solution to the non-stationarity problem has also the feature of revealing immediately to the economist the longrun properties of the estimated model. To see this point practically we can use E-Views to simulate the following bivariate model:
$$
\begin{aligned}
\Delta c_{t} &=0.25 \Delta y_{t}-0.2\left(c_{t-1}-y_{t-1}\right)+0.003 u_{1 t} \
\Delta y_{t} &=0.02+0.009 u_{2 t}
\end{aligned}
$$
经济代写|宏观经济学作业代写Macroeconomics代考|Cointegration in a multivariate framework
So far we have stressed the importance of the magnitude of the adjustment parameter $\alpha$ as the relevant discriminant to decide on cointegration, but we have not yet provided a statistical framework to test for such an hypothesis. We also mentioned the importance of dimensionality of the system to be considered in empirical work. In this section we shall elaborate on these points and illustrate the Johansen’s $([30],[34])$ approach to cointegration in a multivariate framework.
So far we have considered cointegration in a bi-variate context. Things differ when we consider a multivariate context. In fact, in general between $n$ nonstationary series we can have up to $n-1$ cointegrating vector and the single equation dynamic modelling can cause serious troubles when there are multiple cointegrating vectors. To illustrate the problem let us consider the case of an investigator who uses cointegration techniques to investigate money demand. Following the standard economic background to empirical investigations of money demand (see, for example, Hendry and Ericsson, [26]) the chosen data set includes money, $m$, a price index, $p$, real income, $y$, the own interest rate on money, $R^{m}$, and the opportunity cost of holding money, $R^{b}$. All variables are in logarithms,
with the exception of interest rates. The investigator specifies a dynamic singleequation model for real money, towards the identification of a money demand equation, which takes the following shape:
$$
\begin{aligned}
(m-p){t}=& a{0}+a_{1}(m-p){t-1}+a{2} y_{t-1}+a_{3} y_{t-2}+\
&+a_{4} R_{t-1}^{m}+a_{5} R_{t-2}^{m}+a_{6} R_{t-1}^{b}+a_{7} R_{t-2}^{b}+u_{t}
\end{aligned}
$$
This statistical model fits the data well. As it is found that $a_{1}<1$, the investigation leads to the identification of a long-run equilibrium money demand, which results clearly form the ECM re-parametrization of the dynamic model (2.19) : $$ \begin{aligned} \Delta(m-p){t}=& a{0}-a_{3} \Delta y_{t-1}-a_{5} \Delta R_{t-1}^{m}-a_{6} \Delta R_{t-1}^{b}+\ &\left(a_{1}-1\right)\left[(m-p){t-1}-(m-p){t-1}^{}\right]+u_{t} \ (m-p){t-1}^{}=& \frac{a{2}+a_{3}}{1-a_{1}} y_{t-1}+\frac{a_{4}+a_{5}}{1-a_{1}} R_{t-1}^{m}+\frac{a_{6}+a_{7}}{1-a_{1}} R_{t-1}^{b}
\end{aligned}
$$
However, the good fit of the statistical model might be combined with an incorrect identification of the long-run solution. Think, for example, of the case in which the non-stationary vector containing the five variables of interests admits two cointegration relationships: $(m-p-y)$ and $\left(R^{m}-\beta_{22} R^{b}\right)$. Where the first one is generated by the stationarity of the velocity of circulation of money and the second one by the behaviour of the banking sector, which sets the interest rate on money as a mark-down on the opportunity cost of holding money. In the short-run money reacts to disequilibria with respect to both long-run solutions, hence money demand is correctly parametrised as follows:
$$
\begin{aligned}
\Delta(m-p){t}=& \pi{0}+\pi_{1} \Delta y_{t-1}+\pi_{2} \Delta R_{t-1}^{m}+\pi_{3} \Delta R_{t-1}^{b} \
&-\alpha_{1}\left(m_{t-1}-p_{t-1}-y_{t-1}\right)+\alpha_{2}\left(R_{t-1}^{m}-\beta_{22} R_{t-1}^{b}\right)+u_{t}
\end{aligned}
$$
经济代写|宏观经济学作业代写MACROECONOMICS代考|The Johansen Procedure
To illustrate the procedure proposed by Johansen consider the multivariate generalisation of the single-equation dynamic model discussed so far, i.e. a Vector Autoregressive Model (VAR) for the vector of, possibly non-stationary, mvariables y:
$$
\mathbf{y}{t}=\mathbf{A}{1} \mathbf{y}{t-1}+\mathbf{A}{2} \mathbf{y}{t-2}+\ldots+\mathbf{A}{n} \mathbf{y}{t-n}+\mathbf{u}{t}
$$
by proceeding in the same way we did for the simple single-equation dynamic model, we can reparameterise the VAR in levels as a model involving levels and first-differences of variables.
Start by subtracting $\mathbf{y}{t-1}$ from both sides of the VAR to obtain: $$ \Delta \mathbf{y}{t}=\left(\mathbf{A}{1}-\mathbf{I}\right) \mathbf{y}{t-1}+\mathbf{A}{2} \mathbf{y}{t-2}+\ldots+\mathbf{A}{n} \mathbf{y}{t-n}+\mathbf{u}{t} $$ now subtract $\left(\mathbf{A}{1}-\mathbf{I}\right) \mathbf{y}{t-2}$ from both sides to obtain: $$ \Delta \mathbf{y}{t}=\left(\mathbf{A}{1}-\mathbf{I}\right) \Delta \mathbf{y}{t-1}+\left(\mathbf{A}{1}+\mathbf{A}{2}-\mathbf{I}\right) \mathbf{y}{t-2}+\ldots+\mathbf{A}{n} \mathbf{y}{t-n}+\mathbf{u}{t}
$$
By iterating this procedure until $n-1$, we end up with the following specification:
$$
\begin{aligned}
\Delta \mathbf{y}{t} &=\Pi{1} \Delta \mathbf{y}{t-1}+\Pi{1} \Delta \mathbf{y}{t-2}+\ldots+\ &=\sum{i=1}^{n-1} \Pi_{i} \Delta \mathbf{y}{t-i}+\Pi \mathbf{y}{t-n}+\mathbf{u}{t} \end{aligned} $$ where : $$ \begin{aligned} &\Pi{i}=-\left(I-\sum_{j=1}^{i} \mathbf{A}{j}\right) \ &\Pi=-\left(I-\sum{i=1}^{n} \mathbf{A}_{i}\right)
\end{aligned}
$$
宏观经济学代写
经济代写|宏观经济学作业代写MACROECONOMICS代考|COINTEGRATION AND ERROR CORRECTION MODELS
为了解释为什么在估计动态模型时虚假结果会消失,让我们考虑为消耗估计的动态规范的简化版本:
C吨=一种0+一种1C吨−1+一种2是吨+一种3是吨−1+在吨
这个规范有一些有趣的动态特性值得讨论。首先请注意,消费相对于收入的短期弹性不同于长期弹性。事实上,短期弹性是一种2而长期弹性为一种2+一种31−一种1. 通过设置动态模型中的所有变量来找到长期弹性2.14到它们的稳态值C吨+一世=C¯,是吨+一世=C¯. 要立即看到这一点,请考虑以下重新参数化:ΔC吨=一种0+一种2Δ是吨−一种(C吨−1−b1是吨−1)+在吨 一种=(1−一种1),b1=一种2+一种31−一种1
估计的动态模型包括一阶差分和水平。水平变量的存在会生成一个长期解决方案,通过将所有一阶差分设置为零来得出
$\beta_{1} y_{t-1}$ as the long-run equilibrium level $c^{}$ for the log of real consumption $c$. When $\alpha<0$ consumption increases at time t whenever $c_{t-1}}$, and decreases whenever $c_{t-1}>c_{t-1}^{}$. The system equilibrates in presence of disequilibrium (i.e. a discrepancy between $c$ and $c^{}$ ) such error correction features guarantees that in the long-run the consumption will converge to its equilibrium value. For this reason the specification (2.15), with $\alpha<0$, is termed Error Correction Model. Note that, in the case of an ECM representation, the difference between $c$ and $c^{*}$ is a stationary series. This defines co-integration. We say that two non stationary variables integrated of order $q$ are cointegrated of order $p$ if there exist a linear combination of them which is integrated of order $p-q$. The case $p=1, q=1$, is interesting in that co-integration implies an ECM representation, which allows to re-write a model in levels, which involves non-stationary time-series, as a model which involves only stationary variables. Such variables are stationary either because they are first diferences of non-stationary variables or because they are stationary linear combination of non-stationary variables (cointegrating vectors).
在估计关系中同时包含差异和水平是解决与规范中包含的变量水平的非平稳性有关的问题的关键因素。这种非平稳性问题的解决方案还具有立即向经济学家揭示估计模型的长期性质的特点。要实际看到这一点,我们可以使用 E-Views 来模拟以下双变量模型:
ΔC吨=0.25Δ是吨−0.2(C吨−1−是吨−1)+0.003在1吨 Δ是吨=0.02+0.009在2吨
经济代写|宏观经济学作业代写MACROECONOMICS代考|COINTEGRATION IN A MULTIVARIATE FRAMEWORK
到目前为止,我们已经强调了调整参数幅度的重要性一种作为决定协整的相关判别式,但我们尚未提供统计框架来检验这种假设。我们还提到了在实证工作中要考虑的系统维度的重要性。在本节中,我们将详细阐述这些观点并说明约翰森的([30],[34])多变量框架中的协整方法。
到目前为止,我们已经考虑了双变量上下文中的协整。当我们考虑多变量上下文时,情况会有所不同。其实一般来说介于n我们最多可以有非平稳序列n−1当存在多个协整向量时,协整向量和单方程动态建模会造成严重的问题。为了说明这个问题,让我们考虑一个使用协整技术来调查货币需求的调查员的案例。遵循标准经济背景对货币需求进行实证研究s和和,F这r和X一种米pl和,H和ndr是一种nd和r一世Css这n,[26]选择的数据集包括金钱,米, 价格指数,p, 实际收入,是, 自己的货币利率,R米,以及持有货币的机会成本,Rb. 所有变量都是对数,
利率除外。研究人员为真实货币指定了一个动态单方程模型,以识别货币需求方程,其形式如下:
$$
\begin{aligned}
(m-p){t}=& a{0}+a_{1}(m-p){t-1}+a{2} y_{t-1}+a_{3} y_{t-2}+\
&+a_{4} R_{t-1}^{m}+a_{5} R_{t-2}^{m}+a_{6} R_{t-1}^{b}+a_{7} R_{t-2}^{b}+u_{t}
\end{aligned}
$$
This statistical model fits the data well. As it is found that $a_{1}<1$, the investigation leads to the identification of a long-run equilibrium money demand, which results clearly form the ECM re-parametrization of the dynamic model (2.19) : $$ \begin{aligned} \Delta(m-p){t}=& a{0}-a_{3} \Delta y_{t-1}-a_{5} \Delta R_{t-1}^{m}-a_{6} \Delta R_{t-1}^{b}+\ &\left(a_{1}-1\right)\left[(m-p){t-1}-(m-p){t-1}^{}\right]+u_{t} \ (m-p){t-1}^{}=& \frac{a{2}+a_{3}}{1-a_{1}} y_{t-1}+\frac{a_{4}+a_{5}}{1-a_{1}} R_{t-1}^{m}+\frac{a_{6}+a_{7}}{1-a_{1}} R_{t-1}^{b}
\end{aligned}
$$
However, the good fit of the statistical model might be combined with an incorrect identification of the long-run solution. Think, for example, of the case in which the non-stationary vector containing the five variables of interests admits two cointegration relationships: $(m-p-y)$ and $\left(R^{m}-\beta_{22} R^{b}\right)$. Where the first one is generated by the stationarity of the velocity of circulation of money and the second one by the behaviour of the banking sector, which sets the interest rate on money as a mark-down on the opportunity cost of holding money. In the short-run money reacts to disequilibria with respect to both long-run solutions, hence money demand is correctly parametrised as follows:
$$
\begin{aligned}
\Delta(m-p){t}=& \pi{0}+\pi_{1} \Delta y_{t-1}+\pi_{2} \Delta R_{t-1}^{m}+\pi_{3} \Delta R_{t-1}^{b} \
&-\alpha_{1}\left(m_{t-1}-p_{t-1}-y_{t-1}\right)+\alpha_{2}\left(R_{t-1}^{m}-\beta_{22} R_{t-1}^{b}\right)+u_{t}
\end{aligned}
$$
经济代写|宏观经济学作业代写MACROECONOMICS代考|THE JOHANSEN PROCEDURE
为了说明 Johansen 提出的程序,考虑到目前为止讨论的单方程动态模型的多元推广,即向量自回归模型在一种R对于可能是非平稳的 m 变量 y 的向量:
$$
\mathbf{y}{t}=\mathbf{A}{1} \mathbf{y}{t-1}+\mathbf{A}{2} \mathbf{y}{t-2}+\ldots+\mathbf{A}{n} \mathbf{y}{t-n}+\mathbf{u}{t}
$$
by proceeding in the same way we did for the simple single-equation dynamic model, we can reparameterise the VAR in levels as a model involving levels and first-differences of variables.
Start by subtracting $\mathbf{y}{t-1}$ from both sides of the VAR to obtain: $$ \Delta \mathbf{y}{t}=\left(\mathbf{A}{1}-\mathbf{I}\right) \mathbf{y}{t-1}+\mathbf{A}{2} \mathbf{y}{t-2}+\ldots+\mathbf{A}{n} \mathbf{y}{t-n}+\mathbf{u}{t} $$ now subtract $\left(\mathbf{A}{1}-\mathbf{I}\right) \mathbf{y}{t-2}$ from both sides to obtain: $$ \Delta \mathbf{y}{t}=\left(\mathbf{A}{1}-\mathbf{I}\right) \Delta \mathbf{y}{t-1}+\left(\mathbf{A}{1}+\mathbf{A}{2}-\mathbf{I}\right) \mathbf{y}{t-2}+\ldots+\mathbf{A}{n} \mathbf{y}{t-n}+\mathbf{u}{t}
$$
By iterating this procedure until $n-1$, we end up with the following specification:
$$
\begin{aligned}
\Delta \mathbf{y}{t} &=\Pi{1} \Delta \mathbf{y}{t-1}+\Pi{1} \Delta \mathbf{y}{t-2}+\ldots+\ &=\sum{i=1}^{n-1} \Pi_{i} \Delta \mathbf{y}{t-i}+\Pi \mathbf{y}{t-n}+\mathbf{u}{t} \end{aligned} $$ where : $$ \begin{aligned} &\Pi{i}=-\left(I-\sum_{j=1}^{i} \mathbf{A}{j}\right) \ &\Pi=-\left(I-\sum{i=1}^{n} \mathbf{A}_{i}\right)
\end{aligned}
$$
$$

经经济代写|宏观经济学作业代写Macroeconomics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。